UP Board Solutions for Class 7 Maths Chapter 11 वृत्त
These Solutions are part of UP Board Solutions for Class 7 Maths. Here we have given UP Board Solutions for Class 7 Maths Chapter 11 वृत्त.
अभ्यास 11 (a)
प्रश्न 1.
पाश्र्व चित्र में Oवृत्त का केन्द्र है। निम्नलिखित कथनों में सत्य/असत्य कथनों को बताइएः
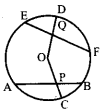
(i) रेखाखंड AB जीवा है। (✓)
(ii) QF त्रिज्या है। (✗)
(iii) OD त्रिज्या है। (✓)
(iv) PC जीवा है। (✗)
प्रश्न 2.
अर्धवृत्त में बने कोण की माप होती है।
(i) 30°
(ii) 60°
(iii) 180°
(iv) 90° (✓)
प्रश्न 3.
आकृति 11.5 के अनुसार अपनी अभ्यास पुस्तिका पर एक आकृति खींचकर उसके दीर्घ वृत्तखंड को छायांकित कीजिए।

उत्तर :
चित्र में दीर्घ वृत्तखंड ADB है।
प्रश्न 4.
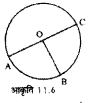
आकृति 11.6 में 0 वृत्त का केन्द्र है। आकृति में निर्मित किन्हीं दी त्रिज्यखंडों के नाम लिखिए।
उत्तर :
चित्र में निर्मित्त दो त्रिज्यखंड OAB तथा OBC है।
प्रश्न 5.
2.5 सेमी त्रिज्या का एक वृत्त खींचिए जिसका केन्द्र 0 है। इस वृत्त को दो अर्द्धवृत्तों में विभक्त कीजिए।
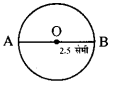
रचना – सर्वप्रथम 0 को केन्द्र मानकर 2.5 सेमी त्रिज्या का एक वृत्त खींचा। AP वृत्त का व्यास AB खींचा, जिससे वृत्त दो भागों में विभक्त होगा।
प्रश्न 6.
आकृति 11.7 में 0 वृत्त का केन्द्र है। ∠ACB कितने अंश का है? अपने उत्तर के पक्ष में कारण बताइए।
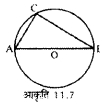
उत्तर :
चूँकि अर्द्धवृत्त में बना कोण समकोण होता है,
अतः ∠ACB = 90°
अभ्यास 11 (b)
प्रश्न 1.
अर्द्धवृत्त का अंशमाप होता है।
(i) 45°
(ii) 90°
(iii) 180°
(iv) 360°
उत्तर :
(iii) 180°
प्रश्न 2.
किसी वृत्त में यदि उसके किसी लघुचाप का अंशमाप 70° है, तो उसके दीर्घचाप का अंशमाप कितना होगा?
हल :
लघुचाप का अंशमाप = 70°
दीर्घचाप का अंशमाप = 360° – 70° = 290°
प्रश्न 3.
किसी चाप द्वारा केन्द्र पर अन्तरित कोण तथा उसके द्वारा वृत्त के शेष भाग पर स्थित किसी बिन्दु पर अन्तरित कोण में क्या सम्बन्ध होता है?
उत्तर :
किसी चाप द्वारा केन्द्र पर अन्तरित कोण उसके द्वारा वृत्त के शेष भाग पर स्थित किसी बिन्दु पर अन्तरित कोण का दो गुना होता है।
प्रश्न 4.
आकृति 11.17 में 0 वृत्त का केन्द्र है। चाप AXB को अंशमाप बताइए।
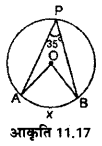
हल :
∠APB = 35°
चाप AXB का अंशमाप = ∠ AOB
= 2 ∠ APB
= 2 × 35° = 70°
प्रश्न 5.
आकृति 11.18 में लधुचाप BCD एवं दीर्घचाप BAD के अन्तर्गत कोणों के नाम बताइए।
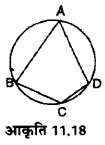
हल :
लघुचाप BCD के अन्तर्गत कोण = ∠ BCD
दीर्घचाप BAD के अन्तर्गत कोण = ∠ BAD
प्रश्न 6.
आकृति 11.19 में o वृत्त का केन्द्र है। A, C और B वृत पर तीन बिन्दु है, तथा ∠AOB को प्रतिवर्ती कोण = 240° है तो ACB का मान ज्ञात कीजिए।
हल :
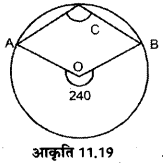
∠ACB = ∠ AOB
∴ ∠ACB = × 240 = 120°
अभ्यास 11 (c)
प्रश्न 1.
आकृति 11.25 में एक ही वृत्तखंड में बने कोणों के नाम लिखिए।”
हल :
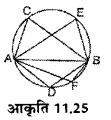
∠ ACB और ∠ AEB एक ही वृत्तखंड में बने दीर्घ कोण हैं तथा ∠ ADB और ∠AFB एक ही वृत्तखंड में बने लघुकोण हैं।
प्रश्न 2.
आकृति 11.26 मे बने कोण PRQ=45°, तो ∠PSQ का मान बताइए।
हल :
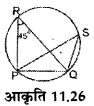
चूँकि एक ही वृत्तखंड में बने कोण बराबर होते हैं।
अतः ∠ PSQ = ∠ PRQ = 45°
प्रश्न 3.
आकृति 11.27 में यदि ∠ACB=x, तो ∠ADB एवं ∠AEB के मान बताइए।
हल :
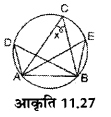
चूंकि एक ही वृत्तखंड में बने कोण बराबर होते हैं। अतः
∠ ADB = ∠ ACB = x°
∠AEB = ∠ ACB = x°
प्रश्न 4.
आकृति 11.28 में बने कोणों के सम्बन्ध में निम्नलिखित कथनों में सत्य/असत्य कथनों को छाँटिएः
उत्तर :
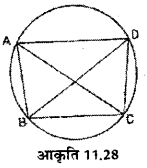
(i) ∠BDC = ∠BAC – सत्य
(ii) ∠BDC = ∠BCA – असत्य
(iii) ∠ACB = ∠ADB – सत्य
(iv) ∠BDA = ∠CDB – असत्य
(v) ∠ACD = ∠DBA – सत्य
प्रश्न 5.
आकृति 11.29 में ∠ACB के बराबर निम्नलिखित में से कौन-सा कोण है?
(i) ∠ABD
(ii) ∠ADB
(iii) ∠DBC
(iv) ∠BAD
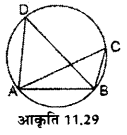
उत्तर :
(ii) ∠ADB
दक्षता अभ्यास – 11
प्रश्न 1.
आकृति 11.32 में वृत्त को केन्द्र 0 है। रेखा BOD, ∠AOC की समद्विभाजक है, तथा ∠COD=50°, तो ∠ABC की माप होगीः
(i) 50°
(ii) 25°
(iii) 100°
(iv) 120°
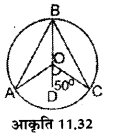
हल :
∠ AOC = 2 ∠ COD= 2 × 50° = 100°
∴ ∠ ABC = ∠ AOC =
× 100° = 50° (i)
प्रश्न 2.
आकृति 11.33 में AB वृत्त की जीवा है बिन्दु C तथा D वृत्त पर हैं। यदि ∠ADB = 45° तो ∠ACB की माप होगीः
(i) 90°
(ii) 135°
(iii) 45०
(iv) 223°

हल :
∠ ACB =∠ ADB = 45° (iii)
प्रश्न 3.
आकृति 11.34 में बिन्दु 0 वृत्त का केन्द्र है और ∠AOB = 60°, तो ∠ADB की माप होगीः
(i) 120°
(ii) 150°
(iii) 140°
(iv) 30°

हल :
वृहत्त कोण AOB = 360° -∠ AOB = 360° – 60° = 300°
∴ ∠ ADB = × बृहत AOB =
× 300° = 150° (ii)
प्रश्न 4.
आकृति 11.35 में बिन्दू 0 वृत्त का एक केन्द्र है। इस पर तीन बिन्दु A, B तथा C हैं। यदि ∠ACB = 40° तो ∠AOB की माप होगीः
(i) 20°
(ii) 40°
(iii) 60°
(iv) 80°

हल :
∠AOB = 2 ∠ ACB = 2 × 40° = 80° (iv)
प्रश्न 5.
आकृति 11.36 में बिन्दु 0 वृत्त का एक केन्द्र है। वृत्त की दो समान जीवाए AC और BC खींची गई हैं। ∠ABC का मान ज्ञात कीजिए।
हल :
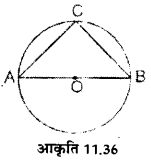
चूँकि अर्द्धवृत्त का कोण समकोण होता है ∠ACB = 90°
प्रश्नानुसार, AC = BC4∠ CAB = ∠ABC
∠CAB + ∠ABC + ∠ ACB = 180°
∠ABC + ∠ABC + 90° = 180°
∠ ABC = 180° – 90° = 90°
∠ABC = = 45०
प्रश्न 6.
निम्नांकित वृत्तों में प्रत्येक का केन्द्र 0 है। प्रत्येक में x का मान ज्ञात कीजिए।
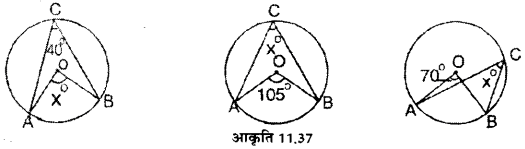
हलः
(i) x° = ∠AOB = 2 ∠ACB = 2 × 40° = 80°
(ii) x° = ∠ACB = 1/2 ∠AOB = × 105° = 52.5°
(iii) x° = ∠ACB = 1/2 ∠AOB = × 70° = 35°
प्रश्न 7.
वृत्त की एक जीवा की लम्बाई उसकी त्रिज्या के बराबर है। इस जीवा द्वारा लघु वृत्तखंड पर अन्तरित कोण ज्ञात कीजिए।
हल :
चूंकि वृत्त की जीवा AB वृत्त की त्रिज्या के बराबर है। अत: ∆OAB समबाहु त्रिभुज होगा तथा तीनों कोण बराबर होंगे।
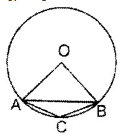
∠OAB +∠OBA+∠AOB = 180°
∠AOB +∠AOB +∠AOB = 180°
3∠AOB = 180°
∠AOB = ![]() = 60°
= 60°
बृहत्त कोण AOB = 360° – ∠ AOB = 360° – 60° = 300°
∠ACB = 3 बृहत्त ∠AOB = ![]() × 300° = 150°
× 300° = 150°
अतः लघु वृत्तखंड पर अन्तरित कोण = 150°
प्रश्न 8.
3.0 सेमी त्रिज्या का एक वृत्त खींचिए। इस वृत्त की:एक जीवा । खींचकर वृत्त को दो वृतखंडों में विभक्त कीजिए।
हल :
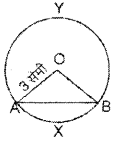
सर्वप्रथम सेमी त्रिज्या लेकर परकार की सहायता से एक वृत्त खींचा। किसी भी लम्बाई की एक जीवा AB खींची। अत: वृत्त, दीर्घ वृत्तखंड AYB तथा लघु वृत्तखंडे AXB में विभाजित हो गया।
प्रश्न 9.
अर्द्धवृत्त किसे कहते हैं? चित्र बनाकर स्पष्ट कीजिए।
उत्तर :
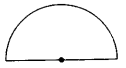
वृत्त के आधे भाग को अर्द्धवृत्त कहते हैं।
प्रश्न 10.
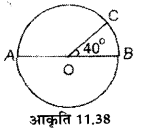
आकृति 11.38 में बिन्दु 0 वृत्त का केन्द्र हैं। AOB वृत्त का व्यास है और ∠COB=40°। ज्ञात कीजिए:
(i) दीर्घचाप BC का अंशमाप
(ii) दीर्घचाप AC को अंशमाप
(iii) लघुचाप AC का अंशमाप
(iv) अर्द्धवृत्त ACB का अंशमाप।
हल :
(i) दीर्घचाप BC का अंशमाप = 360° – 40° = 320°
(ii) दीर्घचाप AC का अंशमाप = 360° – 140° = 220°
(iii) लघुचाप AC का अंशमाप = 360°-220° = 140°
(iv) अर्धवृत्त ACB का अंशमाप = 180°
प्रश्न 11.
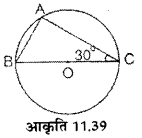
आकृति 11.39 में 0 वृत्त का केन्द्र है। इसके अन्तर्गत एक AABC बना है यदि ∠ACB= 30° तो ∠A और ∠B ज्ञात कीजिए।
हल :
चूँकि अर्द्धवृत्त का कोण समकोण होता है।
अतः ∠A = 90°
∠ACB + ∠ BAC + ∠ABC = 180°
30° + 90° + ∠ABC = 180°
120° + ∠ABC = 180°
∠ABC = 180° – 120° = 60°
प्रश्न 12.
वृत्त की एक जीवा की लम्बाई उसकी त्रिज्या के बराबर है। इस जीवा द्वारा दीर्घ वृत्तखंड पर अन्तरित कोण ज्ञात कीजिए।
हल :
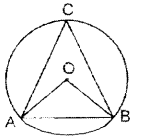
चूंकि वृत्त की जीवा AB वृत्त की त्रिज्या के बराबर है। अत: ∆OAB समबाहु त्रिभुज होगा तथा तीनों कोण बराबर होंगे।
∠AOB = 60°
अतः दीर्घ वृतखंड पर अन्तरित कोण = x 60° = 30°
प्रश्न 13.
आकृति 11.40 में 0 वृत्त का केन्द्र है। ∠AEB= 130° और ∠EBC=20°, तो ∠BDA का मान ज्ञात कीजिए।
हल :
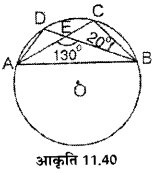
∠ AEB +∠ BEC = 180°
130° +∠ BEC = 180°
∠ BEC = 180° – 130° = 50°
∆ BEC में, 2 ECB +∠ BEC +∠ EBC = 180°
∠ ECB + 50° +20° = 180°
∠ACB =∠ ECB = 180° – 70° = 110°
∠ BDA =∠ ACB = 110°
प्रश्न 14.
आकृति 11.41 में 0 वृत्त को केन्द्र है। ∠ABC=40° और ∠CAB= 80°, तो ∠ADB का मान ज्ञात कीजिए।
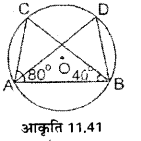
हल :
∆ABC में,
∠ ABC + ∠CAB +∠ ACB = 180°
40° + 80° + 2 ACB = 180°
120° + 2 ACB = 180°
∠ ACB = 180° – 120° = 60°
प्रश्न 15.
आकृति 11.42 में 0 वृत्त का केन्द्र है तथा AABC एक समबाहु त्रिभुज है ∠BOC का मान ज्ञात कीजिए।
हल :
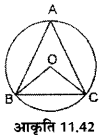
चूँकि A ABC एक समबाहु त्रिभुज है। अतः त्रिभुज के तीनों कोण बराबर होंगे।
∴ ∠ BAC = ![]() = 60°
= 60°
∠ BOC = 2 ∠ BAC = 2 × 60° = 120°
प्रश्न 16.
आकृति 11.43 में 0 वृत्त का केन्द्र है और ∠BOD=130°, ∠BCD का माप ज्ञात कीजिए।
हल :
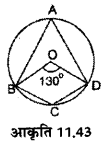
अधिक कोण ∠ BOD = 130°
वृहत कोण ∠ BOD = 360° – 130° = 230°
∠ BCD = 1/2 ∠ BOD
= ![]() × 230° = 115°
× 230° = 115°
प्रश्न 17.
आकृति 11.44 में 0 वृत्त का केन्द्र है। ∠OBC=40°, तो ∠BAC का माप ज्ञात कीजिए।
हल :
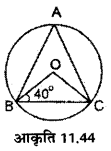
A OBC में ∠OCB = ∠OBC= 40°
∠ OBC +∠OCB +∠ BOC = 180°
40° + 40° +∠ BOC = 180°
80° +∠ BOC = 180°
∠ BOC = 180° – 80° = 100°
∠ BAC = ![]() ∠ BOC
∠ BOC
= ![]() × 100° = 50°
× 100° = 50°
We hope the UP Board Solutions for Class 7 Maths Chapter 11 वृत्त help you.