These Solutions are part of UP Board Solutions for Class 8 Maths. Here we have given UP Board Solutions for Class 8 Maths Chapter 16 संभावना (प्रायिकता).

संभावना (प्रायिकता)

अभ्यास – 16 (a)

प्रश्न 1.
एक सिक्का कई बार उछालकर उसके शीर्ष (चित्र) तथा पूँछ (पट) आने की संख्या निम्नांकित सारणी में लिखी गई है। अपनी अभ्यास पुस्तिका में सारणी में रिक्त स्थानों की पूर्ति कीजिए।
उत्तर

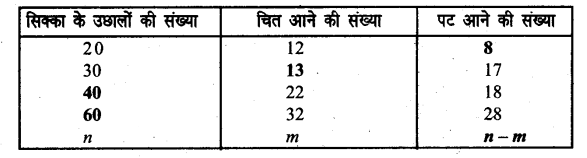
प्रश्न 2.
एक पाँसे को कई बार फेंककर उसके ऊपर आने वाली संख्याएँ आगे अंकित सारणी में लिखी गई है। अपनी अभ्यास पुस्तिका में सारणी में रिक्त स्थान की पूर्ति कीजिए –
उत्तर

प्रश्न 3.
एक समांगी पाँसे के 48 बार फेंकने पर प्रत्येक फलक के ऊपर आने की संभावनाओं को समान मान लेने पर ज्ञात कीजिए कि अंक. 1, 2, 3, 4, 5, 6 में से प्रत्येक कितनी बार ऊपर आएगा?
उत्तर
अंकों की संख्या 6
पाँसा फेंका गया = 48 बार
∴ प्रत्येक अंक दिए पाँसों की संख्या = 48 ÷ 6 = 8 बार

प्रश्न 4.
एक समांगी पाँसे के 54 बार फेंकने पर यह पाया गया कि सम अंकों के ऊपर आने की संख्या 25 है, तो ज्ञात कीजिए कि विषम अंकों के ऊपर अपने की कुल संख्या कितनी होगी?
उत्तर
कुल फेंके गए पाँसे = 54 बार
सम अंकों के लिए फेंके गए पाँसे = 25 बार
∴ विषम अंकों के लिए फेंके गए पाँसों की संख्या = 54-25 = 29 बार।

अभ्यास – 16 (b)

प्रश्न 1.
दो सिक्के एक साथ 40 बार उछाले गए। यदि HH, HT, TH क्रमशः :9,8, 12 बार आए हों, । तो ज्ञात कीजिए कि TT कितनी बार आया होगा?
उत्तर
सिक्के उछाले गए = 40 बार
तीन परिणामों (HH, HT, TH) के लिए उछाले गए सिक्के (9+8+12) = 29 बार
∴ TT के लिए उछाले गए सिक्के = 40-29 = 11 बार

प्रश्न 2.
एक सिक्का 1000 बार उछाला गया और पाया गया कि चित 455 बार आया। ज्ञात कीजिए पट आने का प्रतिशत कितना है?
उत्तर
सिक्के उछाले गए = 1000 बार
सिक्के के चित आने की संख्या = 455
पट आने की संख्या = 1000 – 455 = 545
∴ 1000 बार उछालने पर पट आने की संख्या = 545
तो 100 बार उछालने पर पट आने का प्रतिशत =x100 = 54.5%

प्रश्न 3.
दो सिक्कों को एक साथ 400 बार उछालने पर देखा गया कि
दो चित                    90 बार
एक चित                  210 बार
कोई भी चितं नहीं   100 बार
इनसे प्रत्येक घटना के घटित होने का प्रतिशत ज्ञात कीजिए।
उत्तर

प्रश्न 4.
एक पाँसे को 1000 बार फेंकने पर प्राप्त परिणामों 1,2,3,4,5,6 बारम्बारताएँ निम्नांकित सारणी में दी हुई हैं। 1, 2, 3, 4, 5, 6 में प्रत्येक के आने का प्रतिशत ज्ञात कीजिए।

उत्तर

प्रश्न 5.
दो पाँसे एक साथ फेंके जाते हैं और पाँसों पर ऊपर आने वाले अंकों का योगफल लिया जाता है। निम्नांकित घटनाओं को समुच्चय के रूप में लिखिए –
(i) प्राप्त योग सम संख्या हो,
(ii) प्राप्त योग 3 का अपवर्त्य हो,
(iii) प्राप्त योग 4 से न्यून हो,
(iv) प्राप्त योग 10 से अधिक हो,
उत्तर
शिक्षक की सहायता से शिक्षार्थी स्वयं करें ।।

प्रश्न 6.
तीन सिक्के एक साथ उछाले जाते हैं तो निम्नांकित घटनाओं को समुच्चय के रूप में लिखिए।
(i) कोई चित प्रकट नहीं होता,
(ii) केवल एक चित होता है,
(iii) कम से कम दो चित प्रकट होते हैं,
(iv) तीनों चित आते हैं।
उत्तर

1. कोई चित प्रकट नहीं होता से आशय है कि तीनों पूँछ है = TTT
2. दो पूँछ और दर्शाए = HTT, THT, TTH
3. एक पूँछ और दर्शाए = HHT, HTH, HHT
4. तीनों सिर = HHH

प्रश्न 7.
दो पाँसों को एक साथ फेंकने पर दोनों पर सम अंकों के ऊपर आने की घटना का समुच्चय ज्ञात कीजिए।
उत्तर
दूसरे, चौथे व छठे बार फेंके जाने वाले पाँसों पर सम अंक 2, 4, 6= (2, 2), (2,4), (2,6), (4, 2), (4,4), (4, 6), (6, 2), (6, 4), (6, 6)

प्रश्न 8.
दो पाँसों को एक साथ फेंकने पर दोनों पर विषम अंकों के ऊपर आने की घटना का समुच्चय लिखिए।
उत्तर
प्रथम, तीसरी व पाँचवी बार फेंके जाने वाले पाँसों पर विषम अंक 1, 3, 5= (1,1), (1,3), (1,5), (3, 1), (3, 3), (3, 5), (5, 1), (5, 3), (5, 5)

प्रश्न 9.
दो पाँसों को एक साथ फेंकने पर दोनों पर अंकों का योग विषम संख्या आने का समुच्चय लिखिए।
उत्तर
पहले पाँसे पर सम अंक, दूसरे पर विषम अंक, तीसरे पर सम अंक, चौथे पर विषम अंक, पाँचवें पर सम और छठे पर विषम अंक रखने पर = (1,2), (1,4), (1,6), (2, 1), (2, 3), (2,5), (3, 2), (3,4), (3,6), (4,1), (4, 3), (4, 5), (5, 2), (5,4), (5, 6), (6, 1), (6, 3), (6, 5)

प्रश्न 10.
दो पाँसों को एक साथ फेंकने पर दोनों पर अंकों का योग अभाज्य संख्या होने का समुच्चय लिखिए।
उत्तर
शिक्षार्थी उपरोक्त प्रश्न की तरह हल करें।

प्रश्न 11.
एक लाटरी में 100 इनाम हैं जबकि उसके 100000 टिकट बिके हैं। इस लाटरी का एक टिकट खरीदने वाले व्यक्ति की इनाम जीतने की संभावना कितनी है?
उत्तर
इनाम प्राप्त करने की संभावना =

We hope the UP Board Solutions for Class 8 Maths Chapter 16 संभावना (प्रायिकता) help you. If you have any query regarding UP Board Solutions for Class 8 Maths Chapter 16 संभावना (प्रायिकता), drop a comment below and we will get back to you at the earliest.