UP Board Solutions for Class 10 Maths Chapter 2 Polynomials
These Solutions are part of UP Board Solutions for Class 10 Maths. Here we have given UP Board Solutions for Class 10 Maths Chapter 2 Polynomials.
प्रश्नावली 2.1 (NCERT Page 31)
प्र. 1. किसी बहुपद p(x) के लिए, y = p(x) का ग्राफ नीचे आकृति 2.10 में दिया गया है | प्रत्येक स्थिति में, p(x) के शुन्यकों की संख्या ज्ञात कीजिए |

हलः
(i) दिया गया ग्राफ -अक्ष के समान्तर है।
यह x-अक्ष को किसी भी बिन्दु पर प्रतिच्छेद नहीं करता है।
शून्यकों की संख्या = 0
(ii) दिया गया p(x) का ग्राफ x-अक्ष को केवल एक बिन्दु पर काटता है।
p(x) के शून्यांकों की संख्या =1
(iii) p(x) का ग्राफ x-अक्ष को तीन बिन्दुओं पर काटता है।
p(x) के शून्यांकों की संख्या = 3
(iv) p(x) का ग्राफ x-अक्ष को दो बिन्दुओं पर काटता है।
p(x) के शून्यांकों की संख्या = 2
(v) p(x) का ग्राफ x-अक्ष को चार बिन्दुओं पर काटता है।
p(x) के शून्यांकों की संख्या = 4
(vi) p(x) का ग्राफ -अक्ष को तीन बिन्दुओं पर काटता है।
p(x) के शून्यांकों की संख्या = 3

प्रश्नावली 2.2 (NCERT Page 36)
प्र. 1. निम्न द्विघात बहुपदों के शुन्यक ज्ञात कीजिए और शुन्यकों तथा गुणांकों के बीच संबंध की सत्यता की जाँच कीजिए |
(i) x² – 2x – 8
(ii) 4s² – 4s +1
(iii) 6x² – 3 – 7x
(iv) 4u² +8u
(v) t² – 15
(vi) 3x² – x – 4







प्र. 2. एक द्विघात बहुपद ज्ञात कीजिए, जिसके शुन्यकों के योग तथा गुणनफल क्रमश: दी गई संख्याएँ हैं :
(i) , -1
(ii) √2,
(iii) 0, √5
(iv) 1, 1
(v) ,
(vi) 4, 1


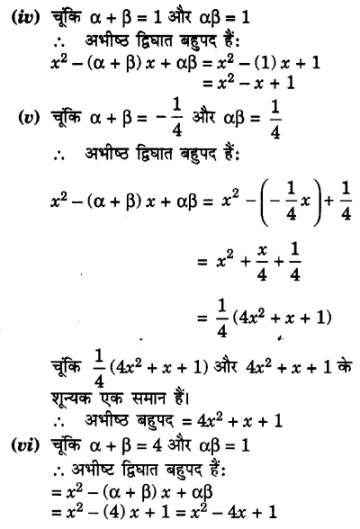
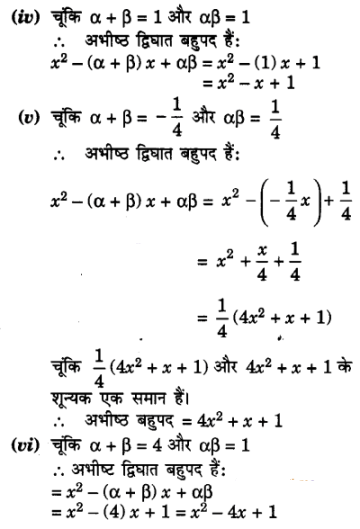
प्रश्नावली 2.3 (NCERT Page 39)
प्र. 1. विभाजन एल्गोरिथम का प्रयोग करके, निम्न में p(x) को g(x) से भाग देने पर भागफल तथा शेषफल ज्ञात कीजिए :
(i) p(x) = x3 – 3x2 + 5x – 3, g(x) = x2 – 2
(ii) p(x) = x4 – 3x2 + 4x + 5, g(x) = x2 + 1 – x
(iii) p(x) = x4 – 5x + 6, g(x) = 2 – x2
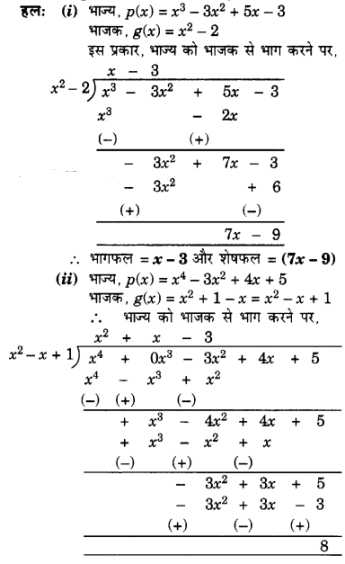

प्र. 2. पहले बहुपद से दुसरे बहुपद को भाग करके, जाँच कीजिए कि क्या प्रथम बहुपद द्वितीय का एक गुणनखंड है :
(i) t2 – 3, 2t4 + 3t3 – 2t2 – 9t – 12
(ii) x2 + 3x + 1, 3x4 + 5x3 – 7x2 + 2x + 2
(iii) x3 – 3x + 1, x5 – 4x3 + x2 + 3x + 1






प्र. 4. यदि x3 – 3x2 + x + 2 को एक बहुपद g(x) से भाग देने पर, भागफल और शेषफल क्रमश: x – 2 और – 2x + 4 हैं तो g(x) ज्ञात कीजिए।
हल :
दिया है : भाज्य p(x) = x3 – 3x2 + x + 2
भागफल q(x) = x – 2,
शेषफल r(x) = -2x + 4
भाजक g(x) = ?
भाज्य = भाजक × भागफल + शेषफल
p(x) = g(x) × q(x) + r(x)
x3 – 3x2 + x + 2 = g(x) (x – 2) + (- 2x + 4)
x3 – 3x2 + x + 2 + 2x – 4 = g(x) (x – 2)
g(x) (x – 2) = x3 – 3x2 + 3x – 2

प्र. 5. बहुपदों p(x), g(x), q(x) और r(x) के ऐसे उदाहरण दीजिए जो विभाजन एल्गोरिथम को संतुष्ट करते हों तथा
(i) घात p(x) = घात q(x) हो
(ii) घात q(x) = घात r(x) हो
(iii) घात r(x) = 0
हलः विभाजन एल्गोरिथ्म को संतुष्ट करते हुए प्रत्येक का एक-एक उदाहरण इस प्रकार हैः ।

प्रश्नावली 2.4 (NCERT Page 40)
प्र. 1. सत्यापित कीजिए कि निम्न त्रिघात बहुपदों के साथ दी गई संख्याएँ उसकी शून्यक हैं। प्रत्येक स्थिति में शून्यकों और गुणांकों के बीच के संबंध् को भी सत्यापित कीजिए:
(i) 2x3 + x2 – 5x + 2; , 1, -2;
(ii) x3 – 4x2 + 5x – 2; 2, 1, 1



प्र० 2. एक त्रिघात बहुपद प्राप्त कीजिए जिसके शून्यकों का योग, दो शून्यकों को एक साथ लेकर उनके गुणनफलों का योग तथा तीनों शून्यकों के गुणनफल क्रमशः 2, -7, -14 हों।

प्र० 3. यवि बहुपव x3 – 3x2 + x + 1 के शून्यक a – b, a, a + b हों, तो a और b ज्ञात कीजिए।
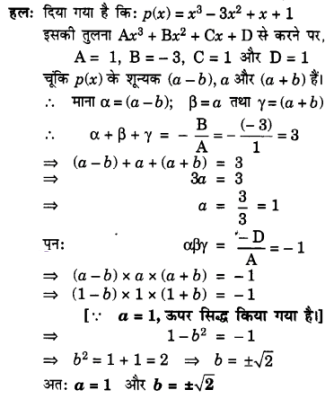
प्र० 4. यदि बहुपद x4 – 6x3 – 26x2 + 138x – 35 के दो शून्यक 2 ± √3 हों, तो अन्य शून्यक ज्ञात कीजिए।

प्र० 5. यदि बहुपद x4 – 6x3 + 16x2 – 25x + 10 को एक अन्य बहुपद x2 – 2x + k से भाग दिया जाए और शेषफल x + a आता हो, तो k तथा a ज्ञात कीजिए।

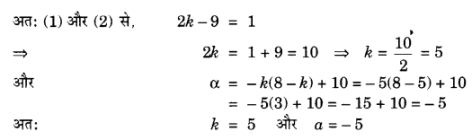
Hope given UP Board Solutions for Class 10 Maths Chapter 2 are helpful to complete your homework.
If you have any doubts, please comment below. UP Board Solutions try to provide online tutoring for you.