UP Board Solutions for Class 7 Maths Chapter 8 व्यंजकों का गुणनफल एवं सर्वसमिकाएँ
These Solutions are part of UP Board Solutions for Class 7 Maths. Here we have given UP Board Solutions for Class 7 Maths Chapter 8 व्यंजकों का गुणनफल एवं सर्वसमिकाएँ.
अभ्यास 8 (a)
प्रश्न 1.
निम्नांकित के मान बताइए।
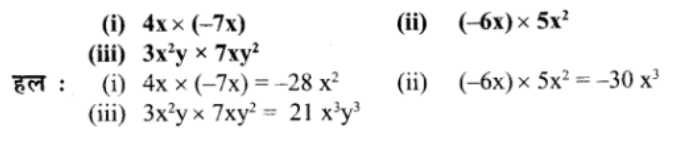
प्रश्न 2.
गुणनफल ज्ञात कीजिए।

प्रश्न 3.
निम्नांकित के गुणनफल ज्ञात कर माने ज्ञात कीजिए।

प्रश्न 4.
एक खेत में 2x क्यारियाँ हैं। प्रत्येक क्यारी में x y पंक्तियाँ हैं। प्रत्येक पंक्ति में y’ टमाटर के पौधे लगे हैं। ज्ञात कीजिए|
(i) खेत में कुल कितने पौधे लगे हैं?
हल :
खेत में पौधों की कुल संख्या = क्यारियाँ x पंक्तियाँ x पौधों की संख्या
= 2x × xy × xy
= 2 × x1+1 × y1+2 = 2x2y3 पौधे
(ii) यदि x = 3, y = 2, तो पौधों की संख्या कितनी है?
हल :
पौधों की संख्या = 2x2y3
= 2x (3)2 × (2)3
= 2 x 9 x 8 = 144 पौधे
अभ्यास 8 (b)
प्रश्न 1.
गुणी कीजिए:

प्रश्न 2.
सरल कीजिए:

प्रश्न 3.
सरल कीजिए :
(i) 2x (3x + 5y) – 5y (2x – 3y)
हल :
2x (3x + 5y) – 5y × (2x – 3y)
= 6x2 + 10xy – 10xy + 15y2 = 6x2 + 15y2
(ii) x (y – z) + 2y (z-x) + z (x -y)
हल :
x × (y – z) + 2y × (z – x) + z × (x – y)
= xy – xz + 2yz – 2xy + xz – yz = -xy + yz
(iii) y2 (y2 +1) – y3 (y +1) + y (y2 – y)
हल :
y2 × (y2 +1) – y3 × (y +1) + y × (y2 – y)
= y4 +y2 – y4 – y3 + y3 – y2 = 0
(iv) x (1+x2) – x2 – (x – 1) – (x +x2)
हल :
x (1+x2) – x2 × (x – 1) – (x +x2)
= x + x3 – x3 + x2 – x – x2 = 0
प्रश्न 4.
एक विद्यालय में 2x कक्षाएँ हैं। प्रत्येक कक्षा में विद्यार्थियों की संख्या (x2 + 2x +2) है। ज्ञात कीजिए :
(i) विद्यालय में विद्यार्थियों की कुल संख्या कितनी है?
हल :
विद्यालय में कक्षाएँ = 2x
प्रत्येक कक्षा में विद्यार्थी = (x2 + 2x + 2)
अत: विद्यालय में कुल विद्यार्थियों की संख्या = 2x × (x3 + 2x + 2)
= 2x4 + 4x2 +4x विद्यार्थी
(ii) यदि x = 3, तो विद्यालय में कुल कितने विद्यार्थी हैं?
हल :
विद्यार्थियों की संख्या = 2x4 + 4x2 +4x
यदि x = 3, तो कुल विद्यार्थियों की संख्या = 2 (3)4 +4 (3)2 +4 x 3
= 2 x 81 + 4 × 9+ 12
= 162 + 36 + 12 = 210
प्रश्न 5.
एक रेलगाड़ी की चाल (2x2 + x + 4) किमी प्रति घण्टा है। ज्ञात कीजिए:
(i) वह 3x घण्टे में कितनी दूरी तय करेगी?
हल :
रेलगाड़ी की चाल = (2x2 + x +4) किमी/घण्टा
अत: 3x घण्टे में चली गई दूरी = (2x2 + x + 4) x 3x
= 6x2 + 3x2 + 12x किमी
(ii) यदि x = 5, तो उपर्युक्त समय में रेलगाड़ी की चली गई दूरी ज्ञात कीजिए।
हल :
यदि x = 5 तो रेलगाड़ी द्वारा चली गई दूरी।
= 6x2 + 3x2 + 12x = 6 (5)3 +3 (5)2 + 12 x 5
= 6 × 125 + 3 × 25 + 60 = 750 + 75 + 60 = 885 किमी
प्रश्न 6.
एक न्याय पंचायत में 2x + 3 ग्राम सभाएँ हैं। प्रत्येक ग्राम सभा में x+5x+6 नलकूप हैं। तो न्याय पंचायत में कुल कितने नलकूप हैं?
हल :
एक ग्राम सभा में नलकूपों की संख्या = x2+ 5x +6
(2x+3) ग्राम सभाओं में नलकूपों की संख्या = (x2 + 5x +6) × (2x+3)
= 2x3 + 10x2 + 12x + 3x2 + 15x + 18
= 2x2 + 13x2 + 27x + 18
प्रश्न 7.
एक विकास खण्ड में 5x+3 विद्यालय में स्वच्छता के कारण प्रत्येक विद्यालय में 5x-3 बालिकाएँ बढ़ जाती हैं। तो विकास खण्ड में कितनी बालिकाएँ बढ़ जाती हैं?
हल :
एक विद्यालय में स्वच्छता के कारण बालिकाएँ बढ़ जाती हैं = (5x – 3)
(5x+3) विद्यालय में स्वच्छता के कारण बालिकाएँ बढ़ जाती हैं = (5x – 3) (5x + 3)
= 25x2 – 15x + 15x – 9
= 25x2 – 9
प्रश्न 8.
बाल दिवस के अवसर पर x+5 विद्यालयों के बच्चों द्वारा वृक्षारोपण किया गया। प्रत्येक विद्यालय के बच्चों ने x-5x+25 वृक्ष लगाए, तो बच्चों द्वारा कितने वृक्ष लगाए गए?
हल :
एक विद्यालय के बच्चों ने वृक्ष लगाए = x2 + 5x + 25
(x+5) विद्यालयों के बच्चों ने वृक्ष लगाए = (x2 – 5x + 25) × (x + 5)
= x3 -5x2 + 25x + 5x2 – 25x + 125
= x3 + 125
अभ्यास (c)
गुणनफल ज्ञात कीजिए।
प्रश्न 1.
(x + 2) (x + 5)

प्रश्न 2.
(X – 4) (x + 7)
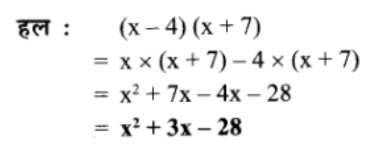
प्रश्न 3.
(x – 3) (x – 8)

प्रश्न 4.
(x2 + 5) (x2 – 7)

प्रश्न 5.
(3x + 8) (4x – 7)
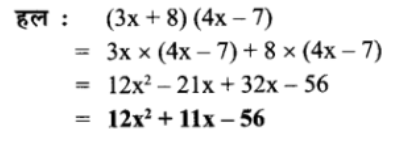
प्रश्न 6.
(5x – 3y) (3x + 4y)
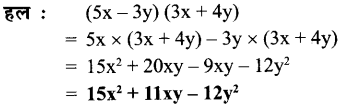
प्रश्न 7.
(x2 + 2xy + y2) (x – y)
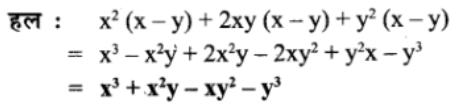
प्रश्न 8.
(2x2 + 3x – 7) (5x + 4)

प्रश्न 9.
(x2 – xy + y2) (x + y) से गुना कीजिए उतर की जाँच कीजिए ,यदि x = 3, y= 2
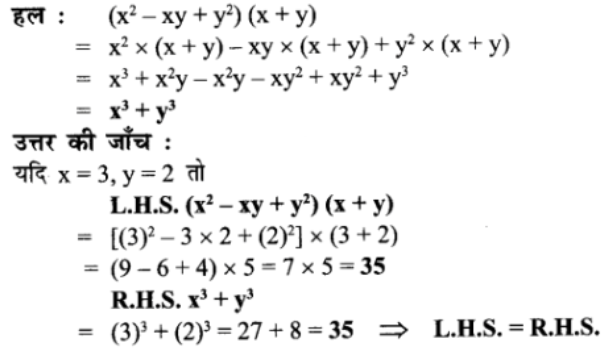
प्रश्न 10.
(x2 + xy + y2) (x2 – xy + y2) से गुना कीजिए उतर की जाँच कीजिए ,यदि x = 2, y= 1
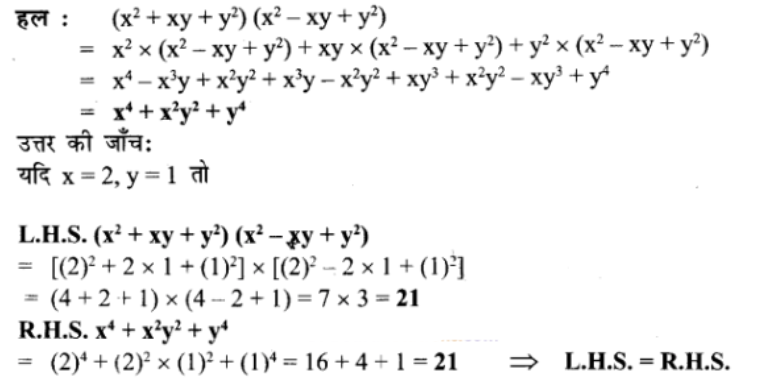
प्रश्न 11.
कविता ने पुस्तक विक्रेता से (3x + 7) कॉपियाँ खरीदीं। यदि प्रत्येक कॉपी का मूल्य (2x – 1) हो, तो।
(i) कुल कॉपियों का मूल्य कितना है?
हल :
कॉपियों की संख्या = (3x +7)
प्रत्येक कॉपी का मूल्य = ₹ (2x – 1)
अतः कॉपियों का कुल मूल्य = (3x + 7) (2x – 1)
= 3x (2x – 1) +7 (2x – 1)
= 6x2 – 3x + 14x -7
= ₹ (6x2 + llx – 7)
(ii) यदि x = 5, तो कविता ने पुस्तक विक्रेता को कितने रुपये दिए?
हल :
यदि x = 5 हो, तो मूल्य = 6x2 + 11x – 7
= 6 (5)2 + 11 (5) -7
= 150 + 55-7
= 205 – 7 = ₹ 198
अभ्यास 8 (d)
प्रश्न 1.
निम्नलिखित में समीकरण तथा सर्वसमिका छाँटकर अपनी अभ्यास पुस्तिका में लिखिए।

प्रश्न 2.
दिखाइए किः (i) 3x (x +1) = 3x2 + 3x एक सर्वसमिका है।

अभ्यास 8 (e)
सर्वसमिका (a + b)2 = a2 + 2ab + b2 की सहायता से मान ज्ञात कीजिएः

प्रश्न 7.
एक बाग में (x + 2y) पंक्तियाँ हैं। प्रत्येक पंक्ति में (x + 2y) पेड़ लगे हैं। ज्ञात कीजिए
(i) बाग में कुल कितने पेड़ हैं?
हल :
बाग में पंक्तियाँ = (x + 2y)
प्रत्येक पंक्ति में पेड़ = (x + 2y)
अतः पेड़ों की कुल संख्या = (x + 2y) (x + 2y) = (x + 2y)2
= x2 + 2 × x × 2y + (2y)2 = x2 + 4xy + 4y2
(ii) यदि x = 3, y = 2, तो बाग में पेड़ों की कुल कितनी संख्या है?
हल :
यदि x = 3. y = 2 है, तो
पेड़ों की कुल संख्या = (x + 2y)2
= (3 + 2 x 2) = (3 +4) = (7)2 = 49
प्रश्न 8.
एक वर्गाकार खेत की भुजा (3x +y) मी लम्बी है। खेत का क्षेत्रफल ज्ञात कीजिए।
हल :
वर्गाकार खेत की भुजा = (3x + y)
खेत को क्षेत्रफल = ( भुजा)2
= (3x + y)2
= (3x)2 + 2x 3x Xy + (y)2
= (9x2 + 6xy + y2) मी2
अभ्यास 8 (f)
सर्वसमिका (a-b)2 = a2 – 2ab + b2 की सहायता से मान ज्ञात कीजिए:

प्रश्न 7.
एक वर्गाकार खेत की एक भुजा की माप (3x – y) मी० है। खेत का क्षेत्रफल ज्ञात कीजिए।
हल : वर्गाकार खेत की भुजा = (3x -y)
खेत का क्षेत्रफल = (भुजा)2
= (3x -y)2
= (3x)2 -2 × 3x × y + (y)2
= (9x2 – 6xy + y2) मी2
प्रश्न 8.
एक खेत में (x – 2y) क्यारियाँ हैं। प्रत्येक क्यारी में (x – 2y) पपीते के पौधे लगे हैं। ज्ञात कीजिए
(i) खेत में कितने पपीते के पौधे हैं?
हल :
क्यारियों की संख्या = (x – 2y)
प्रत्येक क्यारी में पौधों की संख्या = (x – 2y)
अतः खेत में पपीते के पौधों की संख्या = (x – 2y) (x- 2y)
= (x -2y)2
= x2 – 2 × x × 2y + (2y)2
= (x2 – 4xy + 4y2) पौधे ,
(ii) यदि x = 10, y=1, तो कुल पौधों की संख्या कितनी है?
हल :
यदि x = 10, y= 1 है, तो
पौधों की संख्या = x2 – 4xy + 4y2
= (10)2 -4x 10 x 1 +4 (1)2
= 100 -40 +4
= 64 पौधे
प्रश्न 9.
(i) एक कलम का मूल्य र (2x – y) है। इसी प्रकार की (2x – y) कलमों का मूल्य ज्ञात कीजिए।
हल :
1 कलम का मूल्य = (2x – y) रु०
(2x – y) कलमों का मूल्य = (2x -y) (2x -y) ,
= (2x -y)
= (2x)2 – 2 × 2x × y + (y)2
= ₹ (4x2 – 4xy + y2)
(ii) यदि x = 6, y = 2, तो कुल कलमों का कितना मूल्य होगा?
हल :
यदि x = 6, y = 2 है, तो
कलमों का मूल्य = 4x2 – 4xy + y2
= 4 (6)2 – 4 × 6 × 2 + (2)2
= 144 – 48 + 4
= ₹ 100
अभ्यास 8 (g)
सर्वसमिका (a + b) (a – b) = a2 – b2 का प्रयोग करके गुणनफल ज्ञात कीजिएः

प्रश्न 5.
सर्वसमिका का प्रयोग कर (4x + 2y) (4x – 2y) का मान ज्ञात कीजिए, उत्तर की जाँच कीजिए, यदि x = 2,y = 1.
हल :
(4x + 2y) (4x – 2y)
= (4x)2 – (2y)2
= 16x2 – 4y2
उत्तर की जाँच : यदि x = 2, y = 1 तो
L.H.S. (4x + 2y) (4x – 2y)
= (4 × 2 + 2 × 1) (4 × 2 – 2 × 1)
= (8 + 2) (8 – 2) = 10 × 6 = 60
R.H.S. 16x2 – 4y
= 16 (2)2 – 4 (1)2
= 64 – 4 = 60
⇒ L.H.S. = R.H.S.
प्रश्न 6.
एक आयताकार मैदान की लम्बाई (2x + 1) मी तथा चौड़ाई (2x – 1) मी है। आयत का क्षेत्रफल ज्ञात कीजिए।
हल :
आयताकार मैदान की लम्बाई = (2x + 1) मी
आयताकार मैदान की चौड़ाई = (2x – 1) मी
आयताकार मैदार का क्षेत्रफल = (2x + 1) (2x – 1)
= (2x)2 – (1)2 = (4x2 – 1) मी2
प्रश्न 7.
(i) एक पुस्तक का मूल्य १ (3x + 1) है। इसी प्रकार की (3x – 1) पुस्तकों का मूल्य ज्ञाँत कीजिए।
हल :
एक पुस्तक का मूल्य = र (3x + 1)
(3x – 1) पुस्तकों का मूल्य = १ (3x + 1) (3x – 1)
= (3x)2 – (1)2 = ₹ (9x2 – 1)
(ii) यदि x = 3, तो पुस्तकों की संख्या कितनी होगी?
हल :
यदि x = 3 है, तो
पुस्तकों की संख्या = (3x – 1)
= (3 × 3 – 1) = 9 – 1 = 8
(iii) यदि x = 4, तो पुस्तकें खरीदने में कुल कितने रुपये लगे?
हल :
यदि x = 4 है, तो
पुस्तकों का कुल मूल्य = 9x2 -1
[9 x (4)2 – 1] = [(9 x 16) – 1]
= 144-1 = ₹ 143
सर्वसमिकाओं का प्रयोग से निम्नलिखितँ के मान ज्ञात कीजिए:

अभ्यास 8 (h)
सर्वसमिकाओं का प्रयोग करके निम्नांकित के मान ज्ञात कीजिए:



दक्षता अभ्यास 8
निम्नांकित के गुणनफल ज्ञात कीजिए।
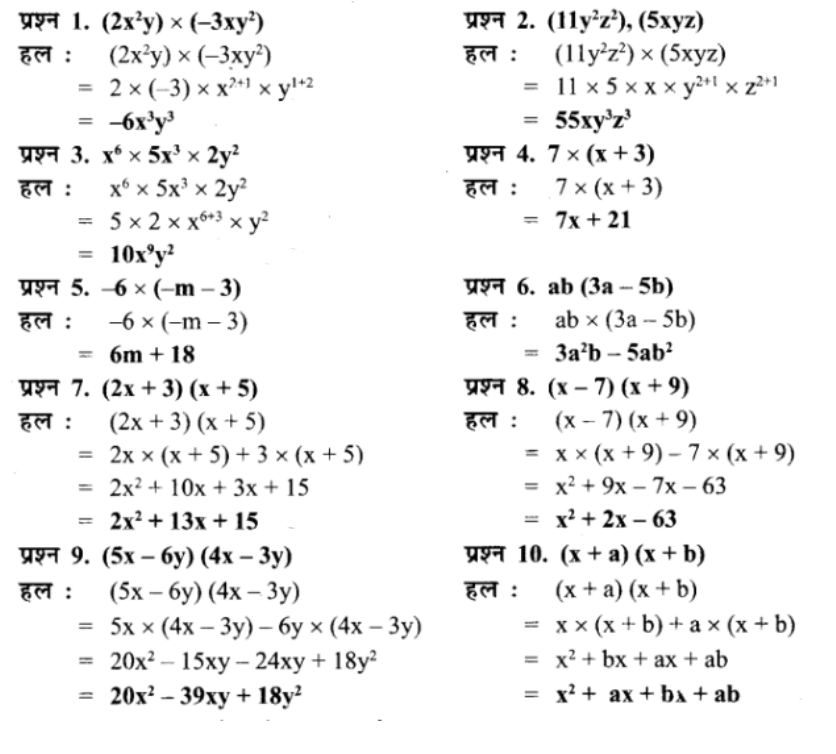

सर्वसमिकाओं के प्रयोग से निम्नलिखित के मान ज्ञात कीजिए।

प्रश्न 19.
निम्नलिखित को सरल कीजिए:
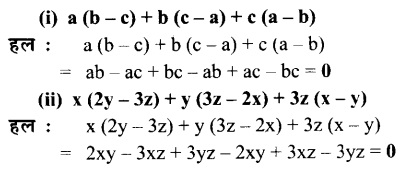
प्रश्न 20.
यदि x + =
, तो x2 +
का मान ज्ञात कीजिए।
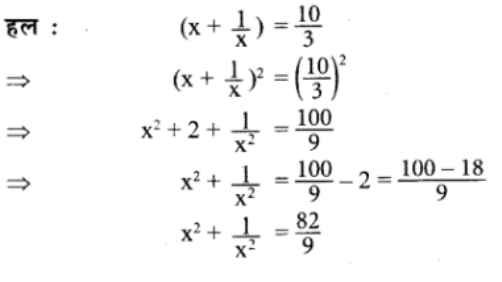
प्रश्न 21. यदि x – =
तो x2 +
का मन ज्ञात कीजिए

प्रश्न 22.
दिखाइये।

(b) (4mn + 3n)2 – (4mn – 3n)2 = 48 mn2

(c) (a-b) (a + b) + (b-c) (b + c) + (e-a) (c+a) = 0
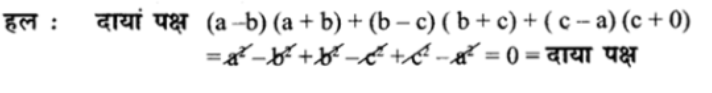
We hope the UP Board Solutions for Class 7 Maths Chapter 8 व्यंजकों का गुणनफल एवं सर्वसमिकाएँ help you.