UP Board Solutions for Class 12 Physics Chapter 1 Electric Charges and Fields (वैद्युत आवेश तथा क्षेत्र)
अभ्यास के अन्तर्गत दिए गए प्रश्नोत्तर
प्रश्न 1.
वायु में एक-दूसरे से 30 cm दूरी पर रखे दो छोटे आवेशित गोलों पर क्रमशः
2 x 10-7 C तथा 3 x 10-7 C आवेश हैं। उनके बीच कितना बल है ?
हल-
दिया है, q1 = 2 x 10-7 C, q2 = 3 x 10-7 C तथा
r = 30 सेमी = 0.3 मीटर, F = ?
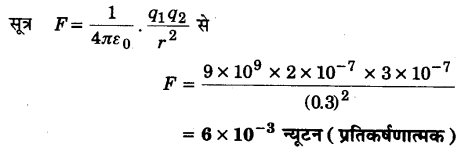
प्रश्न 2.
0.4 μC आवेश के किसी छोटे गोले पर किसी अन्य छोटे आवेशित गोले के कारण वायु में 0.2 N बल लगता है। यदि दूसरे गोले पर 0.8 μC आवेश हो तो
(a) दोनों गोलों के बीच कितनी दूरी है?
(b) दूसरे गोले पर पहले गोले के कारण कितना बल लगता है?
हल-
दिया है, q1 = 0.4 μC = 0.4 x 10-6 C
q2 = 0.8 μC = 0.8 x 10-6 C
तथा q2 के कारण q1 पर बल F = 0.2 N
(a) r = ?

(b) q2 पर -q1 के कारण बल = ?
कूलॉम का बल न्यूटनीय बल है अर्थात् एक आवेश पर दूसरे आवेश के कारण बल, दूसरे आवेश पर पहले आवेश के कारण बले के बराबर तथा विपरीत होता है।
अतः q2 पर q1 के कारण बल भी 0.2 N ही होगा, तथा इसकी दिशा q1 की ओर होगी।
प्रश्न 3.
जाँच द्वारा सुनिश्चित कीजिए कि विमाहीन है। भौतिक नियतांकों की सारणी देखकर इस अनुपात का मान ज्ञात कीजिए। यह अनुपात क्या बताता है?

यह निश्चित दूरी पर रखे इलेक्ट्रॉन व प्रोटॉन के बीच वैद्युत बल तथा गुरुत्वीय बल का अनुपात है। यह बताता है कि गुरुत्वीय बल की तुलना में वैद्युत बल अत्यन्त प्रबल है।
प्रश्न 4.
(a) “किसी वस्तु का वैद्युत आवेश क्वाण्टीकृत है। इस प्रकथन से क्या तात्पर्य है?
(b) स्थूल अथवा बड़े पैमाने पर विद्युत आवेशों से व्यवहार करते समय हम विद्युत आवेश के क्वाण्टमीकरण की उपेक्षा कैसे कर सकते हैं?
उत्तर-
(a) किसी वस्तु का आवेश क्वाण्टीकृत है, इस कथन का तात्पर्य यह है कि हम किसी वस्तु को जितना चाहें उतना आवेश नहीं दे सकते अपितु वस्तु को आवेश, आवेश की न्यूनतम इकाई (e, मूल आवेश) के पूर्ण गुणजों में ही दिया जा सकता है।
(b) स्थूल अथवा बड़े पैमाने पर आवेशों से (UPBoardSolutions.com) व्यवहार करते समय आवेश के क्वाण्टमीकरण का कोई महत्त्व नहीं होता और इसकी उपेक्षा की जा सकती है। इसका कारण यह है कि बड़े पैमाने पर व्यवहार में आने वाले आवेश मूल आवेश की तुलना में बहुत बड़े होते हैं। उदाहरण के लिए 1 μC आवेश में लगभग 1013 मूल आवेश सम्मिलित हैं। ऐसी अवस्था में आवेश को सतत मानकर व्यवहार किया जा सकता है।
प्रश्न 5.
जब काँच की छड़ को रेशम के टुकड़े से रगड़ते हैं तो दोनों पर आवेश आ जाता है। इसी प्रकार की परिघटना का वस्तुओं के अन्य युग्मों में भी प्रेक्षण किया जाता है। स्पष्ट कीजिए कि यह प्रेक्षण आवेश संरक्षण नियम से किस प्रकार सामंजस्य रखता है?
उत्तर-
घर्षण द्वारा आवेशन की घटनाएँ आवेश संरक्षण नियम के साथ पूर्ण सामंजस्य रखती हैं। जब इस प्रकार की किसी घटना में दो उदासीन वस्तुओं को रगड़ा जाता है तो दोनों वस्तुएँ आवेशित हो जाती हैं। घर्षण से पूर्व दोनों वस्तुएँ उदासीन होती हैं अर्थात् उनका कुल आवेश शून्य होता है। (UPBoardSolutions.com) इस प्रकार के सभी प्रेक्षणों में सदैव यह पाया गया है कि एक वस्तु पर जितना धनावेश आता है, दूसरी वस्तु पर उतना ही ऋणावेश आता है। इस प्रकार घर्षण द्वारा आवेशन के बाद भी दोनों वस्तुओं का नेट आवेश शून्य ही बना रहता है।
प्रश्न 6.
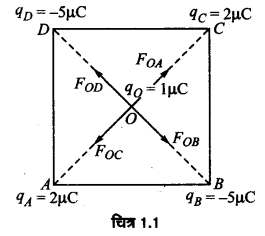
चार बिन्दु आवेश qA = 2 μC, qB = -5 μC, qC = 2 μC तथा qD = -5 μC, 10 cm भुजा के किसी वर्ग ABCD के शीर्षों पर अवस्थित हैं। वर्ग के केन्द्र पर रखे 1 μC आवेश पर लगने वाला बल कितना है ?
हल-
किसी आवेश पर कार्य करने वाले अन्य आवेशों के कारण कूलॉम बलों को सदिश विधि द्वारा जोड़ा जाता है। अत: वर्ग के केन्द्र पर रखे आवेश q0 = 1 μC पर बल चारों आवेशों qA, qB, qC व qD के कारण कूलॉम बलों के सदिश योग के बराबर होगा।


प्रश्न 7.
(a) स्थिर विद्युत-क्षेत्र रेखा एक सतत वक्र होती है अर्थात कोई क्षेत्र रेखा एकाएक नहीं टूट सकती क्यों?
(b) स्पष्ट कीजिए कि दो क्षेत्र रेखाएँ कभी-भी एक-दूसरे का प्रतिच्छेदन क्यों नहीं करतीं?
उत्तर-
(a) विद्युत-क्षेत्र रेखा वह वक्र है जिसके प्रत्येक बिन्दु पर खींची गई स्पर्श रेखा उस बिन्दु पर विद्युत-क्षेत्र की दिशा को प्रदर्शित करती है। ये क्षेत्र रेखाएँ सतत वक्र होती हैं अर्थात् किसी बिन्दु पर एकाएक नहीं टूट सकतीं, अन्यथा उस बिन्दु परे विद्युत-क्षेत्र की कोई दिशा ही नहीं होगी, जो असम्भव है।
(b) दो विद्युत-क्षेत्र रेखाएँ एक-दूसरे को प्रतिच्छेदित नहीं कर सकतीं; क्योंकि इस स्थिति में कटान बिन्दु पर दो स्पर्श रेखाएँ खींची जाएँगी जो उस बिन्दु पर विद्युत-क्षेत्र की दो दिशाएँ प्रदर्शित करेंगी जो असम्भव है।
प्रश्न 8.
दो बिन्दु आवेश qA = 3 μC तथा qB = -3 μC निर्वात में एक-दूसरे से 20 cm दूरी पर स्थित हैं।
(a) दोनों आवेशों को मिलाने वाली रेखा AB के मध्य बिन्दु O पर विद्युत-क्षेत्र कितना है?
(b) यदि 1.5 x 10-9 C परिमाण का कोई ऋणात्मक परीक्षण आवेश इसे बिन्दु पर रखा जाए तो यह परीक्षण आवेश कितने बल का अनुभव करेगा?


प्रश्न 9.
किसी निकाय में दो आवेश qA = 2.5 x 10-7 C तथा qB = – 2.5 x 10-7 C क्रमशः दो बिन्दुओं A : (0, 0, -15 cm) तथा B : (0, 0, +15 cm) पर अवस्थित हैं। निकाय का कुल आवेश तथा विद्युत-द्विध्रुव आघूर्ण क्या है?
हल-
प्रश्नानुसार, qA = 2.5 x 10-7 C, qB = – 2.5 x 10-7 C,
2a = AB = 30 cm = 0.30 m
कुल आवेश, Q = qA + qB = 2.5 x 10-7 C – 2.5 x 10-7 C = 0

प्रश्न 10.
4 x 10-9 cm द्विध्रुव आघूर्ण को कोई विद्युत-द्विध्रुव 5 x 104 NC-1 परिमाण के किसी एकसमान विद्युत-क्षेत्र की दिशा से 30° पर संरेखित है। द्विध्रुव पर कार्यरत बल आघूर्ण का परिमाण परिकलित कीजिए।
हल-
दिया है,

प्रश्न 11.
ऊन से रगड़े जाने पर कोई पॉलीथीन का टुकड़ा 3 x 10-7 C के ऋणावेश से आवेशित पाया गया।
(a) स्थानान्तरित (किस पदार्थ से किस पदार्थ में) इलेक्ट्रॉनों की संख्या आकलित कीजिए।
(b) क्या ऊन से पॉलीथीन में संहति का स्थानान्तरण भी होता है?

(b) हाँ, ऊन से पॉलीथीन पर द्रव्यमान का स्थानान्तरण होता है क्योंकि इलेक्ट्रॉन, जो द्रव्य कण हैं, ऊन से पॉलीथीन पर विस्थापित होते हैं।
m = प्रत्येक इलेक्ट्रॉन का द्रव्यमान = 9.1 x 10-31 kg,
n = 1.875 x 1012
पॉलीथीन पर स्थानान्तरित कुल द्रव्यमान M = m x n = 91 x 10-31 kg x 1.875 x 1012 = 1.71 x 1018 kg
प्रश्न 12.
(a) दो विद्युतरोधी आवेशित ताँबे के गोलों A तथा B के केन्द्रों के बीच की दूरी 50 cm है। यदि दोनों गोलों पर पृथक्-पृथक् आवेश 6.5 x 10-7 C हैं तो इनमें पारस्परिक स्थिर विद्युत प्रतिकर्षण बल कितना है? गोलों के बीच की दूरी की तुलना में गोलों A तथा B की त्रिज्याएँ नगण्य हैं।
(b) यदि प्रत्येक गोले पर आवेश की मात्रा दो गुनी तथा गोलों के बीच की दूरी आधी कर दी जाए तो प्रत्येक गोले पर कितना बल लगेगा?

प्रश्न 13.
मान लीजिए प्रश्न 12 में गोले A तथा B साइज में सर्वसम हैं तथा इसी साइज का कोई तीसरा अनावेशित गोला पहले तो पहले गोले के सम्पर्क, तत्पश्चात दूसरे गोले के सम्पर्क में लाकर, अन्त में दोनों से ही हटा लिया जाता है। अब A तथा B के बीच नया प्रतिकर्षण बल कितना है?
हल-
माना प्रारम्भ में प्रत्येक गोले ‘A’ व ‘B’ पर अलग-अलग q आवेश है। (q = 6.5 x 10-7 C) माना तीसरा अनावेशित गोला C है।
गोले A व C समान आकार के हैं; अतः परस्पर स्पर्श कराने पर ये कुल आवेश (qA + qC = q + 0) को आधा-आधा बाँट लेंगे।
हटाने के तत्पश्चात् दोनों पर आवेश

प्रश्न 14.
चित्र 1.4 में किसी एकसमान स्थिर विद्युत-क्षेत्र में तीन आवेशित कणों के पथचिह्न (tracks) दर्शाए गए हैं। तीनों आवेशों के चिह्न लिखिए। इनमें से किस कण का आवेश-संहति अनुपात () में अधिकतम है?


प्रश्न 15.
एकसमान विद्युत-क्षेत्र E = 3 x 103 iN/C पर विचार कीजिए।
(a) इस क्षेत्र का 10 cm भुजा के वर्ग के उस पाश्र्व से जिसका तल ya तल के समान्तर है, गुजरने वाला फ्लक्स क्या है?
(b) इसी वर्ग से गुजरने वाला फ्लक्स कितना है यदि इसके तल का अभिलम्ब x-अक्ष से 60° का कोण बनाता है?

प्रश्न 16.
प्रश्न 15 में दिए गए एकसमान विद्युत-क्षेत्र का 20 cm भुजा के किसी घन से (जो इस प्रकार अभिविन्यासित है कि उसके फलक निर्देशांक तलों के समान्तर हैं) कितना नेट फ्लक्स गुजरेगा?
उत्तर-
एक घन के 6 फलक होंगे। इनमें से दो फलक y-z समतल के, दो z-x समतल के तथा दो x-y समतल के समान्तर होंगे।
विद्युत-क्षेत्र E = 3 x 10 i N/C x-अक्ष के अनुदिश है; अत: यह z-x तथा x-y समतलों के समान्तर फलकों के समान्तर होगा।
इन चारों फलकों से गुजरने वाला फ्लक्स शून्य होगा।
विद्युत-क्षेत्र एकसमान है; अतः y-z समतल के (UPBoardSolutions.com) समान्तर फलकों में से जितना फ्लक्स एक फलक से अन्दर प्रविष्ट होगा उतनी ही फ्लक्स दूसरे फलक से बाहर आएगा। अतः घन से गुजरने वाला नेट फ्लक्स शून्य होगा।
प्रश्न 17.
किसी काले बॉक्स के पृष्ठ पर विद्युत-क्षेत्र की सावधानीपूर्वक ली गई माप यह संकेत देती है। कि बॉक्स के पृष्ठ से गुजरने वाला नेट फ्लक्स 8.0 x 103 Nm2/C है।
(a) बॉक्स के भीतर नेट आवेश कितना है?
(b) यदि बॉक्स के पृष्ठ से नेट बहिर्मुखी फ्लक्स शून्य है तो क्या आप यह निष्कर्ष निकालेंगे कि बॉक्स के भीतर कोई आवेश नहीं है? क्यों, अथवा क्यों नहीं?

(b) यदि बॉक्स के पृष्ठ से नेट बहिर्मुखी वैद्युत फ्लक्स शून्य है, तो इससे यह निष्कर्ष नहीं निकलता कि बॉक्स के अन्दर कोई आवेश नहीं है। हो सकता है कि बॉक्स के अन्दर समान मात्रा में धनावेश तथा ऋणावेश दोनों उपस्थित हों, जो एक-दूसरे के प्रभाव को निरस्त कर देंगे अर्थात् बॉक्स के अन्दर नेट आवेश शून्य हो जाएगा और हमें ऐसा प्रतीत होगा कि बॉक्स के अन्दर कोई आवेश नहीं है।
प्रश्न 18.
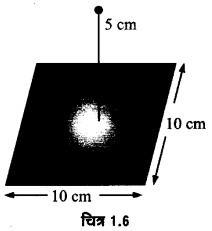
चित्र 1.6 में दर्शाए अनुसार 10 cm भुजा के किसी वर्ग के केन्द्र से ठीक 5 cm ऊँचाई पर कोई +10 µC आवेश रखा है। इस वर्ग से गुजरने वाले विद्युत फ्लक्स का। परिमाण क्या है? [संकेत : वर्ग को 10 cm किनारे के किसी घन का एक फलक मानिए]


प्रश्न 19.
2.0 µC का कोई बिन्दु आवेश किसी किनारे पर 9.0 cm किनारे वाले किसी घनीय गाउसीय पृष्ठ के केन्द्र पर स्थित है। पृष्ठ से गुजरने वाला नेट फ्लक्स क्या है?
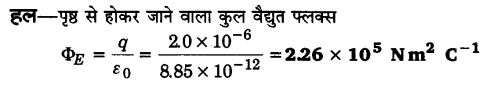
प्रश्न 20.
किसी बिन्द आवेश के कारण, उस बिन्दु को केन्द्र मानकर खींचे गए 10 cm त्रिज्या के गोलीय गाउसीय पृष्ठ पर विद्युत फ्लक्स- 1.0 x 103 Nm2/C
(a) यदि गाउसीय पृष्ठ की त्रिज्या दो गुनी कर दी जाए तो पृष्ठ से कितना फ्लक्स गुजरेगा?
(b) बिन्दु आवेश का मान क्या है?
हल-
(a) बिन्दु आवेश के चारों ओर खींचे गए गोलीय गाउसीय पृष्ठ से गुजरने वाला वैद्युत फ्लक्स उसकी त्रिज्या पर निर्भर नहीं करता, अत: त्रिज्या दो गुनी करने पर भी उससे गुजरने वाला वैद्युत फ्लक्स -1.0 x 108 न्यूटन-मी2/कूलॉम ही रहेगा।

प्रश्न 21.
10 cm त्रिज्या के चालक गोले पर अज्ञात परिमाण का आवेश है। यदि गोले के केन्द्र से 20 cm दूरी पर विद्युत-क्षेत्र 1.5 x 103 N/C त्रिज्यतः अन्तर्मुखी (radially inward) है तो गोले पर नेट आवेश कितना है?
हल-
दिया है, चालक गोले की त्रिज्या R = 10 सेमी
गोले के केन्द्र से बिन्दु की दूरी r = 20 सेमी = 0.20 मी

प्रश्न 22.
2.4m व्यास के एकसमान आवेशित चालक गोले का पृष्ठीय आवेश घनत्व 80.0 µC/m2 है।
(a) गोले पर आवेश ज्ञात कीजिए।
(b) गोले के पृष्ठ से निर्गत कुल विद्युत फ्लक्स क्या है?

प्रश्न 23.
कोई अनन्त रैखिक आवेश 2 cm दूरी पर 9 x 104 NC-1 विद्युत-क्षेत्र उत्पन्न करता है। रैखिक आवेश घनत्व ज्ञात कीजिए।

प्रश्न 24.
दो बड़ी, पतली धातु की प्लेटें एक-दूसरे के समानान्तर एवं निकट हैं। इनके भीतरी फलकों पर, प्लेटों के पृष्ठीय आवेश घनत्वों के चिह्न विपरीत हैं तथा इनका परिमाण 17.0 x 10-23 C/mहै।
(a) पहली प्लेट के बाह्य क्षेत्र में,
(b) दूसरी प्लेट के बाह्य क्षेत्र में, तथा
(c) प्लेटों के बीच में विद्युत-क्षेत्र E का परिमाण परिकलित कीजिए।



अतिरिक्त अभ्यास
प्रश्न 25.
मिलिकन तेल बूंद प्रयोग में 2.55 x 104 NC-1 के नियत विद्युत-क्षेत्र के प्रभाव में 12 इलेक्ट्रॉन आधिक्य की कोई तेल बूंद स्थिर रखी जाती है। तेल का घनत्व 1.26 g cm3 है। बूंद की त्रिज्या का आकलन कीजिए। (g = 9.81 m s-2, e = 1.60 x 10-19 C)।
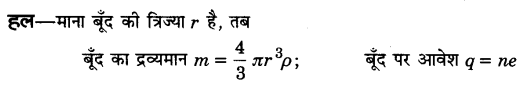
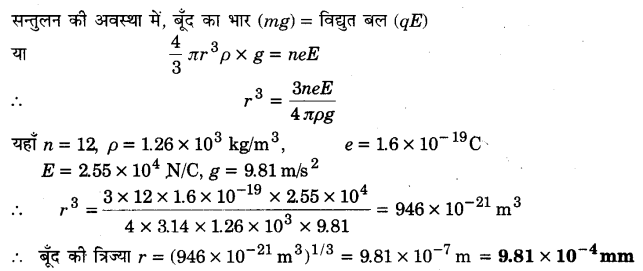
प्रश्न 26.
चित्र 1.9 में दर्शाए गए वक्रों में से कौन सम्भावित स्थिर विद्युत-क्षेत्र रेखाएँ निरूपित नहीं करते?
उत्तर-
केवल चित्र (c) सम्भावित स्थिर विद्युत-क्षेत्र रेखाएँ निरूपित करता है।
(a) विद्युत-क्षेत्र रेखाएँ सदैव चालक पृष्ठ के लम्बवत् होती हैं, इस चित्र में रेखाएँ चालक पृष्ठ के लम्बवत नहीं हैं।
(b) क्षेत्र रेखाओं को ऋणावेश से धनावेश की ओर जाते दिखाया गया है जो कि सही नहीं है।
(d) क्षेत्र रेखाएँ एक-दूसरे को काट रही हैं जो कि सही नहीं है।
(e) क्षेत्र रेखाएँ बन्द वक्रों के रूप में प्रदर्शित की गई हैं जो कि सही नहीं है।
प्रश्न 27.
दिक्स्थान के किसी क्षेत्र में, विद्युत-क्षेत्र सभी जगह z-दिशा के अनुदिश है। परन्तु विद्युत क्षेत्र का परिमाण नियत नहीं है, इसमें एकसमान रूप से z-दिशा के अनुदिश 105 NC-1 प्रति मीटर की दर से वृद्धि होती है। वह निकाय जिसका ऋणात्मक z-दिशा में कुल द्विध्रुव आघूर्ण 10-7 cm के बराबर है, कितना बल तथा बल-आघूर्ण अनुभव करता है?

प्रश्न 28.
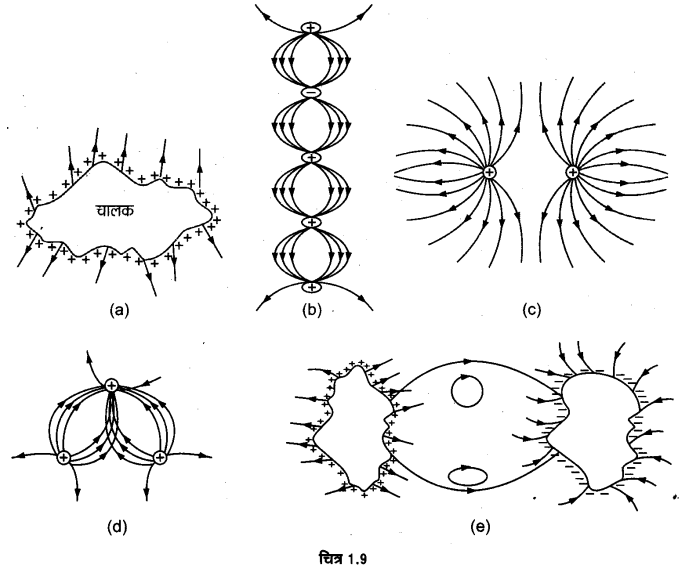
(a) किसी चालक A, जिसमें चित्र 1.10 (a) में दर्शाए अनुसार कोई कोटर/गुहा (Cavity) है, को Q आवेश दिया गया है। यह दर्शाइए कि समस्त आवेश चालक के बाह्य पृष्ठ पर प्रतीत होना चाहिए।
(b) कोई अन्य चालक B जिस पर आवेश q है, को कोटर/गुहा (Cavity) में इस प्रकार सँसा दिया जाता है कि चालक Bचालक A से विद्युतरोधी रहे। यह दर्शाइए कि चालक A के बाह्य पृष्ठ पर कुल आवेश Q + q है [चित्र 1.10 (b)]]
(c) किसी सुग्राही उपकरण को उसके पर्यावरण के प्रबल स्थिर विद्युत-क्षेत्रों से परिरक्षित किया जाना है। सम्भावित उपाय लिखिए।
उत्तर-
(a) एक ऐसी गाउसीय सतह की कल्पना कीजिए जो पूर्णतया चालक के भीतर स्थित है तथा . चालक के बाह्य पृष्ठ के अत्यन्त समीप है।
चालक के भीतर विद्युत-क्षेत्र शून्य होता है; अत: इस गाउसीय सतह से गुजरने वाला नेट विद्युत फ्लक्स शून्य होगा।
तब गाउस प्रमेय से, q = Φ = 0 = 0
अर्थात् सतह के भीतर आवेश शून्य होगा।
अत: चालक का सम्पूर्ण आवेश उसके बाह्य पृष्ठ पर होगा।
(b) दिया है, चालक ‘A’ पर कुल आवेश = Q
चालक ‘B’ पर कुल आवेश = q
माना चालक ‘A’ में बनी कोटर के पृष्ठ पर q1 आवेश है तथा चालक ‘A’ के बाह्य पृष्ठ पर Q1 आवेश है।
अब चालक ‘A’ पर कुल आवेश Q1 + q1 = Q …….(1)
पुन: एक ऐसे गाउसीय पृष्ठ की कल्पना कीजिए जो पूर्णत: चालक ‘A’ के भीतर स्थित है परन्तु इसके बाह्य पृष्ठ के अत्यन्त समीप है।
चालक के भीतर विद्युत-क्षेत्र शून्य होता है; अत: इस पृष्ठ से गुजरने वाला कुल फ्लक्स शून्य होगा।
अत: इस गाउसीय पृष्ठ के भीतर कुल आवेश = 0 अर्थात्
q1 + q = 0 ⇒ q1 = -q
समीकरण (1) से, Q1 – q = Q
चालक ‘A’ के बाह्य पृष्ठ पर कुल आवेश Q1 = Q + q होगा।
(c) खोखले बन्द चालक के भीतर विद्युत-क्षेत्र शून्य होता है; अत: किसी सुग्राही उपकरण को पर्यावरण के प्रबल स्थिर विद्युत-क्षेत्रों से परिरक्षित करने के लिए उसे खोखले बन्द चालक के भीतर रखना चाहिए।
प्रश्न 29.
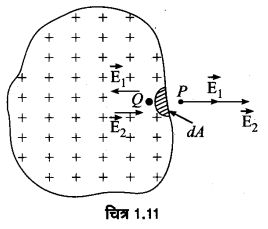
किसी खोखले आवेशित चालक में उसके पृष्ठ पर कोई छिद्र बनाया गया है। यह दर्शाइए कि छिद्र में विद्युत-क्षेत्र है, जहाँ । अभिलम्बवत् दिशा में बहिर्मुखी एकांक सदिश है तथा छिद्र के निकट पृष्ठीय आवेश घनत्व है।
उत्तर-
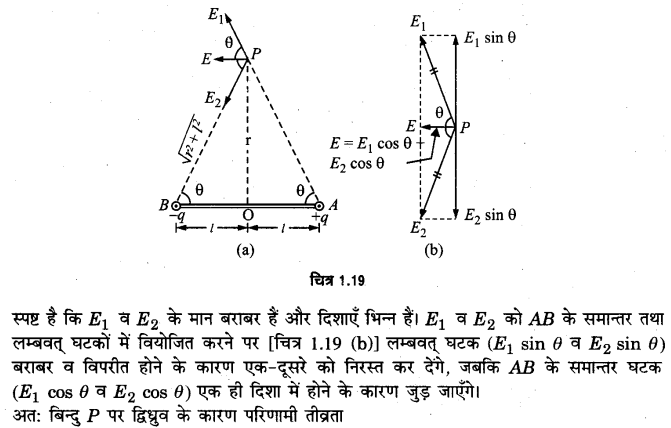
माना किसी खोखले चालक को कुछ धनावेश दिया गया है, जो तुरन्त ही उसके पृष्ठ पर समान रूप से वितरित हो जाता है। माना आवेश का पृष्ठ घनत्व है। चालक के पृष्ठ के किसी अवयव dA पर विचार कीजिए। स्पष्ट है कि इस क्षेत्रफल अवयव पर उपस्थित (UPBoardSolutions.com) आवेश की मात्रा q = dA होगी। माना इस क्षेत्रफल अवयव के अत्यन्त समीप चालक के पृष्ठ के बाहर तथा अन्दर दो बिन्दु क्रमश: P तथा Q हैं। चूँकि बिन्दु P पृष्ठ के समीप है; अतः चालक के कारण बिन्दु P पर विद्युत-क्षेत्र की तीव्रता E = पृष्ठ के लम्बवत् बाहर की ओर होगी। माना बिन्दु P पर अवयव dA तथा शेष चालक के कारण विद्युत-क्षेत्र की तीव्रताएँ क्रमश: E1 व E2 हैं, तब स्पष्टतया E1 व E2 दोनों पृष्ठ के लम्बवत् बाहर की ओर होंगी तथा परिणामी तीव्रता E, E1 व E2 के योग के बराबर होगी।
अतः E1 + E2 = …..(1)
चूँकि बिन्दु Q क्षेत्रफल अवयव dA के अत्यन्त समीप परन्तु P के विपरीत ओर है; अतः इस अवयव के कारण बिन्दु Q पर क्षेत्र की तीव्रता E1 के बराबर परन्तु दिशा में विपरीत होगी, जबकि शेष चालक के कारण Q पर विद्युत-क्षेत्र की तीव्रता E2 के बराबर तथा उसी की दिशा में होगी। चूँकि बिन्दु Q चालक के अन्दर है; अतः बिन्दु Q पर परिणामी तीव्रता शून्य होगी।
अतः बिन्दु Q पर परिणामी तीव्रता E2 – E1 = 0
अथवा E1 = E2 [बिन्दु Q पर E1 व E2 के विपरीत हैं।]
समीकरण (1) से, E1 = E2 =
अतः शेष चालक के कारण बिन्दु P पर विद्युत-क्षेत्र की तीव्रता
E2 =
अब यदि बिन्दु P पर एक छिद्र कर दिया जाए तो क्षेत्र अवयव dA तथा इसके कारण आन्तरिक बिन्दु Q पर विद्युत-क्षेत्र E1 दोनों समाप्त हो जाएँगे।
तब विद्युत-क्षेत्र E2 छिद्र के किसी बिन्दु पर केवल शेष चालक के कारण शेष रहेगा।
अतः छिद्र पर विद्युत-क्षेत्र की तीव्रता
जहाँ n छिद्र पर बहिर्मुखी दिशा में एकांक सदिश है।
प्रश्न 30.
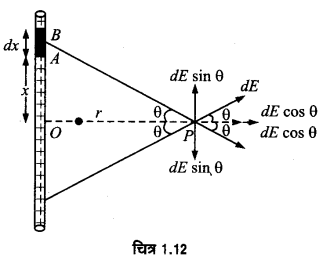
गाउस नियम का उपयोग किए बिना किसी एकसमान रैखिक आवेश घनत्व 2 के लम्बे पतले तार के कारण विद्युत-क्षेत्र के लिए सूत्र प्राप्त कीजिए।
[संकेत : सीधे ही कूलॉम नियम का उपयोग करके आवश्यक समाकलन का मान निकालिए।]
उत्तर-
एकसमान रैखिक आवेश घनत्व वाले लम्बे पतले तार के कारण विद्युत-क्षेत्र (Electric Field due to a Long Straight Wire having Uniform Linear Charge Density)- माना एक लम्बे सीधे धनावेशित तार को एकसमान रैखिक आवेशं घनत्व है। हमें इस तार के कारण किसी बिन्दु P पर विद्युत-क्षेत्र की तीव्रता ज्ञात करनी है। बिन्दु P से तार पर लम्ब PO खींचा। तार पर बिन्दु 0 से x दूरी पर एक सूक्ष्म अवयव AB = dx लिया।


प्रश्न 31.
अब ऐसा विश्वास किया जाता है कि स्वयं प्रोटॉन एवं न्यूट्रॉन (जो सामान्य द्रव्य के नाभिकों का निर्माण करते हैं) और अधिक मूल इकाइयों जिन्हें क्वार्क कहते हैं, के बने हैं। प्रत्येक प्रोटॉन तथा न्यूट्रॉन तीन क्वार्को से मिलकर बनता है। दो प्रकार के क्वार्क होते हैं : ‘अप क्वार्क (u द्वारा निर्दिष्ट) जिन पर + (2/3)e आवेश तथा ‘डाउन क्वार्क (d द्वारा निर्दिष्ट) जिन पर (-1/3) e आवेश होता है, इलेक्ट्रॉन से मिलकर सामान्य द्रव्य बनाते हैं। (कुछ अन्य प्रकार के क्वार्क भी पाए गए हैं जो भिन्न असामान्य प्रकार का द्रव्य बनाते हैं।) प्रोटॉन तथा न्यूट्रॉन के सम्भावित क्वार्क संघटन सुझाइए।

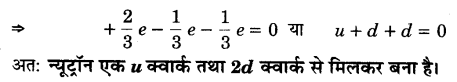
प्रश्न 32.
(a) किसी यादृच्छिक स्थिर विद्युत-क्षेत्र विन्यास पर विचार कीजिए। इस विन्यास की किसी शून्य-विक्षेप स्थिति (null-point अर्थात् जहाँ E = 0) पर कोई छोटा परीक्षण आवेश रखा गया है। यह दर्शाइए कि परीक्षण आवेश का सन्तुलन आवश्यक रूप से अस्थायी है।
(b) इस परिणाम का समान परिमाण तथा चिह्नों के दो आवेशों (जो एक-दूसरे से किसी दूरी पर रखे हैं) के सरल विन्यास के लिए सत्यापन कीजिए।
उत्तर-
(a) माना शून्य विक्षेप स्थिति में रखे परीक्षण आवेश का सन्तुलन स्थायी है। अब यदि परीक्षण आवेश को सन्तुलन की स्थिति से थोड़ा-सा विस्थापित किया जाए तो आवेश पर एक प्रत्यानयन बल लगना चाहिए जो आवेश को वापस सन्तुलन की ओर ले जाए। इसका यह अर्थ हुआ कि (UPBoardSolutions.com) उस स्थान पर शून्य विक्षेप बिन्दु की ओर जाने वाली क्षेत्र रेखाएँ होनी चाहिए। जबकि स्थिर विद्युत-क्षेत्र रेखाएँ कभी भी शून्य विक्षेप बिन्दु तक नहीं पहुँचतीं। अत: हमारी यह परिकल्पना कि परीक्षण आवेश का सन्तुलन स्थायी है, गलत है। यह निश्चित रूप से अस्थायी सन्तुलन है।

प्रश्न 33.
प्रारम्भ में 3-अक्ष के अनुदिश, चाल से गति करती हुई, दो आवेशित प्लेटों के मध्य क्षेत्र में m द्रव्यमान तथा -q आवेश का एक कण प्रवेश करता है (चित्र 1.14 में कण 1 के समान)। प्लेटों की लम्बाई L है। इन दोनों प्लेटों के बीच एकसमान विद्युत-क्षेत्र E बनाए रखा जाता है। दर्शाइए कि प्लेट के अन्तिम किनारे पर कण का ऊर्ध्वाधर विक्षेप है। (कक्षा 11 की पाठ्य पुस्तक के अनुभाग 4.10 में वर्णित गुरुत्वीय क्षेत्र में प्रक्षेप्य की गति के साथ इस कण की गति की तुलना कीजिए।)
उत्तर-
एकसमान विद्युत-क्षेत्र में आवेशित कण (इलेक्ट्रॉन) का गमन-पथ- (i) जब कण का प्रारम्भिक वेग विद्युत-क्षेत्र की दिशा के लम्बवत् है—माना धातु की दो समान्तर प्लेटें जिन पर विपरीत आवेश हैं, एक-दूसरे से कुछ दूरी पर स्थित हैं। इन प्लेटों के बीच के स्थान में विद्युत-क्षेत्र एकसमान है। माना ऊपरी प्लेट धनावेशित है, जबकि नीचे की प्लेट ऋणावेशित है। अत: विद्युत-क्षेत्र E कागज के तल में नीचे की ओर दिष्ट होगा [चित्र 1.14]।


प्रश्न 34.
प्रश्न 33 में वर्णित कण की इलेक्ट्रॉन के रूप में कल्पना कीजिए जिसको vx = 2.0 x 106 ms-1 के साथ प्रक्षेपित किया गया है। यदि 0.5 cm की दूरी पर रखी प्लेटों के बीच विद्युत-क्षेत्र E का मान 9.1 x 102 N/C हो तो ऊपरी प्लेट पर इलेक्ट्रॉन कहाँ टकराएगा? (e = 1.6 x 10-19 C, me = 9.1 x 10-31 kg)

परीक्षोपयोगी प्रश्नोत्तर
बहुविकल्पीय प्रश्न
प्रश्न 1.
इलेक्ट्रॉन के आवेश एवं संहति का अनुपात होगा (2016)
(i) 1.77 x 1011 कूलॉम/किग्रा।
(ii) 1.9 x 1012 कूलॉम/किग्रा
(iii) 1.6 x 10-19 कूलॉम/किग्रा
(iv) 3.2 x 1011 कूलॉम/किग्रा
उत्तर-
(i) 1.77 x 1011 कूलॉम/किग्रा
प्रश्न 2.
दो बिन्दु आवेशों को पहले वायु में तथा फिर K परावैद्युतांक वाले माध्यम में समान दूरी पर रखने पर यदि उनके बीच लगने वाले वैद्युत बल F0 तथा Fm हों तो F0 : Fm का मान होगा
(i) K : 1
(ii) 1 : K
(iii) K2 : 1
(iv) 1 : K2
उत्तर-
(i) K : 1
प्रश्न 3.
वैद्युतशीलता (60) का एस०आई० मात्रक है (2009, 12, 14, 15)
(i) कूलॉम2/न्यूटन-मीटर2
(ii) न्यूटन-मीटर2/कूलॉम2
(iii) न्यूटन/कूलॉम
(iv) न्यूटन/वोल्ट/मीटर2
उत्तर-
(i) कूलॉम2/न्यूटन-मीटर2
प्रश्न 4.
एक निश्चित दूरी r पर स्थित दो समरूप धातु के गोलों पर आवेश +4q तथा -2q हैं। गोलों के बीच आकर्षण बल F है। यदि दोनों गोलों को स्पर्श कराकर पुनः उसी दूरी पर रख दिया जाए तो उनके बीच बल होगा (2015)
(i) F
(ii)
(iii)
(iv)
उत्तर-
(i) F
प्रश्न 5.
दो समान आवेशों q, q को जोड़ने वाली रेखा के मध्य बिन्दु पर एक आवेश q’ रख दिया जाता है। यदि तीनों आवेशों का निकाय सन्तुलन में हो तो q’ का मान होगा- (2011, 18)
(i) -q/2
(ii) -q/4
(iii) +q/4
(iv) +q/2
उत्तर-
(ii) +q/4
प्रश्न 6.
+1 µC तंथा +4 µC के दो आवेश एक-दूसरे से कुछ दूरी पर वायु में स्थित हैं। उन पर लगने वाले बलों का अनुपात है (2014)
(i) 1 : 4
(ii) 4 : 1
(iii) 1 : 1
(iv) 1 : 16
उत्तर-
(iii) 1 : 1
प्रश्न 7.
8 कूलॉम ऋण आवेश में उपस्थित इलेक्ट्रॉनों की संख्या है (2015)
(i) 5 x 1049
(ii) 2.5 x 1019
(iii) 12.8 x 1019
(iv) 1.6 x 1019
उत्तर-
(i) 5 x 1049
प्रश्न 8.
एक वर्ग के दो विपरीत कोनों पर आवेश Q रखे हैं। दूसरे दो विपरीत कोनों पर आवेश q रखे हैं। यदि किसी Q पर नेट विद्युत बल शून्य हो, तो बराबर है
(i)
(ii) -2√2
(iii) -1
(iv) 1
उत्तर-
(ii) -2√2
प्रश्न 9.
वैद्युत-क्षेत्र की तीव्रता का मात्रक है (2011, 13, 15, 16, 17)
(i) कूलॉम/न्यूटन
(ii) जूल/न्यूटन
(iii) न्यूटन/कूलॉम
(iv) न्यूटन/मी
उत्तर-
(iii) न्यूटन/कूलॉम
प्रश्न 10.
निम्न में से कौन-सा वैद्युत-क्षेत्र का मात्रक नहीं है? (2009, 14)
(i) न्यूटन/कूलॉम
(ii) वोल्ट/मीटर
(iii) जूल/कूलॉम
(iv) जूल/कूलॉम/मीटर
उत्तर-
(iii) जूल/कूलॉम
प्रश्न 11.
किसी आवेशित गोलीय चालक में विभव
(i) गोले के भीतर शून्य होता है तथा गोले के बाहर भी शून्य होता है।
(ii) गोले के भीतर अधिकतम होता है तथा गोले के बाहर शून्य होता है।
(iii) गोले के भीतर शून्य होता है तथा गोले के बाहर दूरी बढ़ने के साथ कम होता जाता है।
(iv) गोले के भीतर अधिकतम होता है तथा गोले के बाहर दूरी बढ़ने के साथ कम होता जाता है।
उत्तर-
(iv) गोले के भीतर अधिकतम होता है तथा गोले के बाहर दूरी बढ़ने के साथ कम होता जाता है।
प्रश्न 12.
R1 व R2 त्रिज्याओं के दो चालक गोलों के पृष्ठों पर आवेशों के पृष्ठ घनत्व बराबर हैं। पृष्ठों पर वैद्यत-क्षेत्र की तीव्रताओं का अनुपात है। (2010, 17)
(i)
(ii)
(iii)
(iv) 1 : 1
उत्तर-
(iv) 1 : 1
प्रश्न 13.
आवेश का खोखला गोला वैद्युत क्षेत्र उत्पन्न नहीं करता। (2017)
(i) किसी आन्तरिक बिन्दु पर
(ii) किसी बाहरी बिन्दु पर
(iii) 2 मी से अधिक दूरी पर
(iv) 5 मी से अधिक दूरी पर
उत्तर-
(i) किसी आन्तरिक बिन्दु पर
प्रश्न 14.
r मीटर त्रिज्या वाले खोखले गोले के केन्द्र पर q कूलॉम का आवेश रखा है। यदि गोले की त्रिज्या दोगुनी कर दी जाए तथा आवेश का मान आधा कर दें, तब गोले के पृष्ठ से निर्गत कुल वैद्युत फ्लक्स होगा (2012)
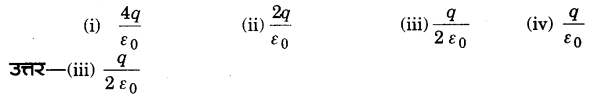
प्रश्न 15.
एक बन्द पृष्ठ के भीतर n वैद्युत द्विध्रुव स्थित हैं। बन्द पृष्ठ से निर्गत वैद्युत फ्लक्स होगा। (2013)
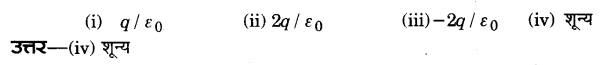
प्रश्न 16.
वैद्युत फ्लक्स को मात्रक है। (2017, 18)

प्रश्न 17.
5 कूलॉम आवेश के दो बराबर तथा विपरीत आवेशों के बीच की दूरी 5.0 सेमी है। इसका वैद्युत द्विध्रुव आघूर्ण है (2015)
(i) 25 x 10-2 कूलॉम-मीटर
(ii) 5 x 10-2 कूलॉम-मीटर
(iii) 1.0 कूलॉम-मीटर
(iv) शून्ये
उत्तर-
(i) 25 x 10-2 कूलॉम-मीटर
प्रश्न 18.
वैद्युत-क्षेत्र में आघूर्ण वाले द्विध्रुव पर लगने वाला बल-आघूर्ण है- (2011, 17, 18)
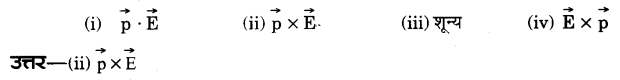
अतिलघु उत्तरीय प्रश्न
प्रश्न 1.
वैद्युत आवेश के क्वाण्टीकरण (quantisation) का मूल कारण क्या है?
उत्तर-
इसका मूल कारण यह है कि एक वस्तु से दूसरी वस्तु में इलेक्ट्रॉनों का स्थानान्तरण केवल पूर्णांक संख्याओं में ही हो सकता है।
प्रश्न 2.
सिद्ध कीजिए कि कूलॉम2/न्यूटन-मीटर2 तथा फैरड/मीटर एक ही भौतिक राशि के मात्रक हैं। (2010)

प्रश्न 3.
बलों के अध्यारोपण का सिद्धान्त क्या है?
उत्तर-
“यदि किसी निकाय में अनेक आवेश हों, तो उनमें से किसी एक आवेश पर बल, अन्य आवेशों के कारण अलग-अलग बलों को सदिश योग होता है, यही बलों के अध्यारोपण का सिद्धान्त कहलाता है।”
प्रश्न 4.
आवेश के रेखीय घनत्व का अर्थ बताइए। (2013)
उत्तर-
किसी चालक अथवा अचालक पदार्थ की प्रति एकांक लम्बाई पर उपस्थित आवेश को उसका रेखीय घनत्व कहते हैं। यदि l लम्बाई के चालक पर एकसमान रूप से फैला हुआ आवेश q हो, तब आवेश का रेखीय घनत्व λ = () कूलॉम/मीटर।
प्रश्न 5.
आवेश के पृष्ठ घनत्व से क्या तात्पर्य है? (2015)
उत्तर-
किसी चालक अथवा अचालक पदार्थ के प्रति एकांक क्षेत्रफल पर उपस्थित आवेश की मात्रा को आवेश का पृष्ठ घनत्व कहते हैं। आवेश का पृष्ठ घनत्व कॅम/मीटर2।
प्रश्न 6.
दो आवेशों के बीच वैद्युत बल का सूत्र लिखिए। प्रयुक्त प्रतीकों के नाम भी लिखिए। (2011)

प्रश्न 7.
कूलॉम के नियम की क्या परिसीमाएँ हैं?
उत्तर-
कूलॉम का नियम दो स्थायी (stationary) वैद्युत आवेशों के लिए सत्य है तथा आवेशों के बीच दूरी r < 10-15 मी के लिए सत्य नहीं है।
प्रश्न 8.
जल का परावैद्युतांक 80 है। वैद्युतशीलता कितनी होगी?
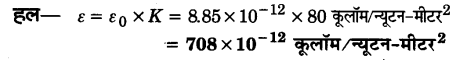
प्रश्न 9.
एक कूलॉम में कितने इलेक्ट्रॉन होते हैं? (2010, 17)
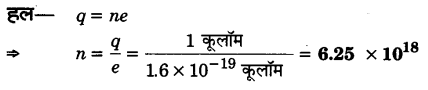
प्रश्न 10.
3.2 कूलॉम आवेश कितने इलेक्ट्रॉनों द्वारा निर्मित होगा ? (2011, 12)

प्रश्न 11.
एक निश्चित दूरी पर स्थित दो इलेक्ट्रॉनों के बीच वैद्युत बल F न्यूटन है। इससे आधी दूरी पर स्थित दो प्रोटॉनों के बीच वैद्युत बल कितना होगा? (2011)

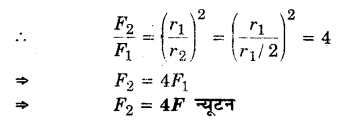
प्रश्न 12.
दो बिन्दु आवेशों के बीच स्थिर वैद्युत बल F है। यदि इन आवेशों को उतनी ही दूरी पर जल (k = 80) में रख दिया जाये तब उनके बीच बल कितना रहेगा? (2014)
हल-
दो बिन्दु आवेशों के बीच स्थिर वैद्युत बल = F
माना जल में रखने पर दोनों बिन्दुओं के बीच स्थिर वैद्युत बल = Fm
Fm = =
प्रश्न 13.
इलेक्ट्रॉन वोल्ट की परिभाषा दीजिए तथा इसका संख्यात्मक मान जूल में व्यक्त कीजिए। (2015)
उत्तर-
एक इलेक्ट्रॉन वोल्ट वह ऊर्जा है जो किसी इलेक्ट्रॉन से 1 वोल्ट विभवान्तर द्वारा त्वरित होने पर अर्जित होती है।
अर्थात् 1 इलेक्ट्रॉन वोल्ट = 1.6 x 10-19 जूल
प्रश्न 14.
कूलॉम के नियम का सदिश रूप बताइए। (2017)
उत्तर-
अत: बिन्दु आवेश q1 पर q2 के कारण कार्यरत वैद्युत बल बिन्दु आवेश q2 पर q1 के कारण कार्यरत वैद्युत बल के परिमाण में बराबर तथा दिशा में विपरीत होता है।
प्रश्न 15.
वैद्युत क्षेत्र की तीव्रता की परिभाषा तथा इसका मात्रक लिखिए। (2015, 17)

प्रश्न 16.
1.5 x 10-3 कूलॉम आवेश पर 2.25 न्यूटन का बल कार्य करता है। उस बिन्दु पर वैद्युत क्षेत्र की तीव्रता ज्ञात कीजिए।

प्रश्न 17.
5.0 x 10-8 कूलॉम बिन्दु आवेश से कितनी दूरी पर वैद्युत क्षेत्र की तीव्रता 450 वोल्ट/मीटर होगी? (2012)

प्रश्न 18.
एक इलेक्ट्रॉन तथा एक प्रोटॉन एक समान वैद्युत क्षेत्र में रखे गए हैं। किसका त्वरण अधिक होगा और क्यों? (2015)
उत्तर-
इलेक्ट्रॉन का त्वरण अधिक होगा, क्योंकि प्रोटॉन की अपेक्षा इलेक्ट्रॉन का द्रव्यमान कम होता है।
प्रश्न 19.
किसी आवेशित कण के भार को एक वैद्युत-क्षेत्र द्वारा किस प्रकार सन्तुलित किया जाता है? (2009)
उत्तर-
कण पर आवेश की प्रकृति के अनुसार उस पर वैद्युत-क्षेत्र ऐसी दिशा में लगाकर, ताकि उसके कारण कण पर लगने वाला वैद्युत बल ऊर्ध्वाधरत: ऊपर की ओर अर्थात् कण के भार की विपरीत दिशा में कार्य करे तथा परिमाण में इसके बराबर हो।
प्रश्न 20.
आवेशित खोखले गोलाकार चालक के भीतर वैद्युत क्षेत्र की तीव्रता कितनी होती है?
उत्तर-
शून्य।
प्रश्न 21.
0.1 मीटर त्रिज्या के एक गोलीय चालक को कितना आदेश दिया जाए कि चालक के पृष्ठ पर वैद्युत-क्षेत्र की तीव्रता900 वोल्ट/मीटर हो जाए ? (2010)
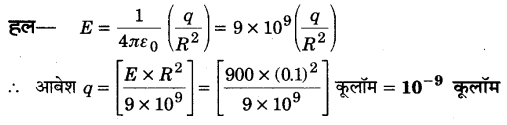
प्रश्न 22.
दो बड़ी पतली धातु की प्लेट एक-दूसरे के बहुत निकट और समान्तर हैं। प्लेटों पर विपरीत प्रकार के आवेश के पृष्ठ घनत्वों के परिमाण 17.7 x 10-22 कूलॉम/मी हैं। प्लेटों के बीच वैद्युत क्षेत्र की तीव्रता क्या है? (2014, 16)

प्रश्न 23.
वैद्युत-फ्लक्स तथा वैद्युत-क्षेत्र की तीव्रता में सम्बन्ध लिखिए। वैद्युत-फ्लक्स का मात्रक भी लिखिए।
या
वैद्युत-फ्लक्स का मात्रक लिखिए। (2018)

प्रश्न 24.
किसी घन के केन्द्र पर 10 μC का एक आवेश रखा है। घन के एक फलक से निकलने वाले वैद्युत-फ्लक्स की गणना कीजिए। (2011)


प्रश्न 26.
यदि किसी 8 सेमी भुजा वाले एक घन के केन्द्र पर 1 कूलॉम आवेश रखा जाए तो घन के किसी फलक से बाहर आने वाले फ्लक्स की गणना कीजिए। (2017)

प्रश्न 27.
एक वैद्युत द्विध्रुव 1.0 x 10-6 कूलॉम परिमाण तथा विपरीत प्रकृति के दो वैद्युत आवेशों से बना है। इन आवेशों के बीच की दूरी 2.0 सेमी है। इस द्विध्रुव को 1.0 x 105 न्यूटन/कूलॉम की बाह्य वैद्युत-क्षेत्र तीव्रता में रखा गया है। द्विध्रुव पर अधिकतम बल-आघूर्ण का मान निकालिए। (2011)
हल-
τmax = pE = (q x 2l) x E
= (1.0 x 10-6 x 2.0 x 10-2) (1.0 x 105)
= 2.0 x 10-3 न्यूटन-मीटर
प्रश्न 28.
1.0 μC के दो बराबर एवं विपरीत प्रकार के आवेश 2.0 मिमी दूर रखे हैं। इस विद्युत द्विध्रुव का द्विध्रुव आघूर्ण ज्ञात कीजिए। (2017)
उत्तर-
दिया है, q = 1.0 μC =1.0 x 10-6 C,
l = 2.0 मिमी = 2 x 10-3 मी
विद्युत द्विध्रुव आघूर्ण, p = q . 2l = 1.0 x 10-6 x 2 x 2 x 10-3 = 4 x 10-9 कूलॉम-मी
प्रश्न 29.
स्थिर वैद्युतिकी में गौस की प्रमेय को गणितीय रूप में लिखिए तथा प्रयुक्त संकेतों के अर्थ बताइए। (2009, 10)

प्रश्न 30.
एक R त्रिज्या वाले Q आवेश से आवेशित धातु के खोखले गोले के केन्द्र से r > R दूरी पर वैद्युत विभव का सूत्र लिखिए। (2013)
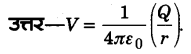
लघु उत्तरीय प्रश्न
प्रश्न 1.
कूलॉम का वैद्युत बल सम्बन्धी नियम लिखिए।
या
दो बिन्दु आवेशों के बीच लगने वाले आकर्षण अथवा प्रतिकर्षण बल के लिए कूलॉम का सूत्र लिखिए।
उत्तर-
कूलॉम का नियम-1785 ई० में फ्रांसीसी वैज्ञानिक कूलॉम ने दो आवेशों के बीच कार्य करने वाले बल के सम्बन्ध में एक नियम दिया, जिसे कूलॉम का नियम कहते हैं। इस नियम के अनुसार-“दो स्थिर बिन्दु आवेशों के मध्य लगने वाला आकर्षण या प्रतिकर्षण बल, दोनों आवेशों की मात्राओं के गुणनफल के अनुक्रमानुपाती तथा उनके बीच की दूरी के वर्ग के व्युत्क्रमानुपाती होता है।” इस बल की दिशा दोनों आवेशों को मिलाने वाली रेखा के अनुदिश होती है। यदि दो बिन्दु आवेश q1 व q2 एक-दूसरे से । दूरी पर स्थित हों, तो कूलॉम के नियम से उनके बीच लगने वाला बल

जहाँ K एक विमाहीन नियतांक है जिसे उस पदार्थ (परावैद्युत माध्यम) का परावैद्युतांक (dielectric constant) अथवा विशिष्ट परावैद्युतता कहते हैं। निर्वात् अथवा वायु के लिए K का मान 1 होता है। उपर्युक्त सूत्र में ε0K के स्थान पर केवल है भी लिखते हैं तथा ६ को परावैद्युत माध्यम की वैद्युतशीलता (permitivity) कहते हैं।
प्रश्न 2.
आसुत जल की 64 बूंदें, प्रत्येक की त्रिज्या 0.1 मिमी तथा आवेश (2/3) x 10-12 कूलॉम है, मिलकर एक बड़ी बूंद बनाती हैं। बड़ी बूंद को विभव ज्ञात कीजिए। (2013)

प्रश्न 3.
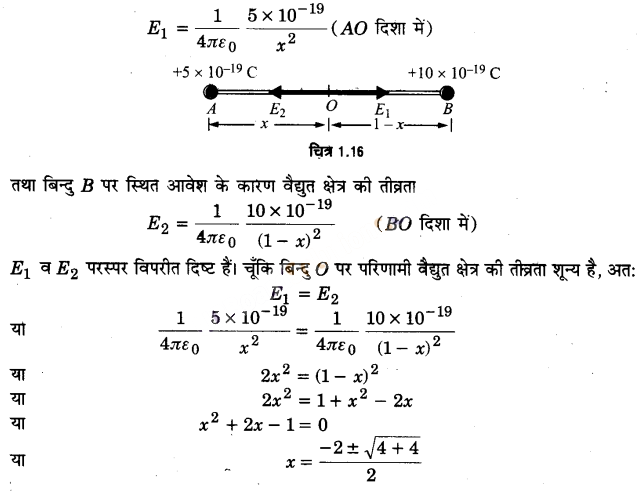
दो बिन्दु आवेश +5 x 10-19 कूलॉम व +10 x 10-19 कूलॉम 1.0 मीटर की दूरी पर पृथकतः स्थित हैं। दोनों आवेशों को जोड़ने वाली रेखा के किस बिन्दु पर विद्युत क्षेत्र की तीव्रता शून्य होगी? (2017)
हल-
माना कि दिये गये बिन्दु आवेश (UPBoardSolutions.com) बिन्दुओं A व B पर स्थित हैं तथा उनके बीच बिन्दु O पर वैद्युत क्षेत्र शून्य है। माना कि बिन्दु0 की बिन्दु A से दूरी x मीटर है; अत: बिन्दु O की बिन्दु B से दूरी (1 – x) मीटर होगी। बिन्दु O पर, बिन्दु A पर स्थित आवेशे के कारण वैद्युत क्षेत्र की तीव्रता

प्रश्न 4.
धातु के एक पतले गोलीय कोश की त्रिज्या 0.25 मीटर है तथा इस पर 0.2 μC आवेश है। इसके कारण एक बिन्दु पर वैद्युत क्षेत्र की तीव्रता ज्ञात कीजिए जबकि बिन्दु
(i) कोश के भीतर,
(ii) कोश के ठीक बाहर तथा
(iii) कोश के केन्द्र से 3.0 मीटर की दूरी पर है। (2017)
हल-
(i) आवेशित कोश के भीतर किसी (UPBoardSolutions.com) भी बिन्दु पर वैद्युत क्षेत्र की तीव्रता शून्य है।
(ii) बाह्य बिन्दुओं के लिए कोश इस प्रकार व्यवहार करता है जैसे कि सम्पूर्ण आवेश इसके केन्द्र पर रखा हो। अत: यदि कोश की त्रिज्या R है, तब कोश के ठीक बाहर किसी बिन्दु पर वैद्युत क्षेत्र की तीव्रता

प्रश्न 5.
वैद्युत-फ्लक्स से क्या तात्पर्य है? इसे आवश्यक सूत्र देते हुए समझाइए। (2009)
या
वैद्युत-फ्लक्स की परिभाषा तथा मात्रक लिखिए। (2012, 15)


प्रश्न 6.
एक समरूप वैद्युत-क्षेत्र E = (5 x 103) i न्यूटन/कूलॉम में एक 10 सेमी भुजा वाला वर्गाकार समतल पृष्ठ yz- तल के समान्तर स्थित है। पृष्ठ से कितना वैद्युत फ्लक्स उत्पन्न होगा? यदि पृष्ठ का तल x-अक्ष की दिशा से 30° कोण बनाता है तब कितना वैद्युत फ्लक्स होगा? (2015)

प्रश्न 7.
एक खोखले बेलन के भीतर q कूलॉम आवेश स्थित है। यदि बेलन के वक्रीय पृष्ठ से वोल्ट-मीटर वैद्युत फ्लक्स सम्बन्धित हो तब बेलन के किसी एक समतल पृष्ठ पर कितना वैद्युत फ्लक्स होगा? (2014)

दीर्घ उत्तरीय प्रश्न
प्रश्न 1.
किसी वैद्युत-द्विध्रुव के कारण अक्षीय स्थिति में किसी बिन्दु पर वैद्युत-क्षेत्र की तीव्रता का व्यंजक प्राप्त कीजिए। (2012, 14)
या
वैद्युत द्विध्रुव के कारण अक्षीय स्थिति में किसी बिन्दु पर वैद्युत क्षेत्र की तीव्रता के सूत्र का निगमन कीजिए। (2013, 16).
उत्तर-
अक्षीय स्थिति में वैद्युत- क्षेत्र की तीव्रता माना कि एक वैद्युत-द्विध्रुव AB, जिसमें (+q) व (-q) कूलॉम के आवेश एक-दूसरे से 2l मीटर की दूरी पर स्थित हैं, किसी ऐसे माध्यम में रखा है जिसका परावैद्युतांक K है। द्विध्रुव की अक्ष पर द्विध्रुव के मध्य बिन्दु O से r मीटर की दूरी पर स्थित (UPBoardSolutions.com) प्रेक्षण बिन्दु P है, जिस पर वैद्युत-क्षेत्र की तीव्रता ज्ञात करनी है (चित्र 1.17)। माना कि द्विध्रुव के आवेश +q व -q के कारण बिन्दु P पर उत्पन्न वैद्युत-क्षेत्र की तीव्रता क्रमशः E1 वे E2 हैं। चित्र 1.17 से स्पष्ट है कि आवेश (+q) से बिन्दु P की दूरी (r – l) है और आवेश (-q) से इसकी दूरी (r + l) है, अतः


प्रश्न 2.
वैद्युत-द्विध्रुव के कारण निरक्षीय स्थिति (अनुप्रस्थ स्थिति) में किसी बिन्दु पर वैद्युत-क्षेत्र की तीव्रता का व्यंजक प्राप्त कीजिए। (2010, 16, 17)
या
वैद्युत-द्विध्रुव की परिभाषा दीजिए। (2014)
उत्तर-
वैद्युत-द्विध्रुव आघूर्ण- वह वैद्युत निकाय (system) जिसमें दो बराबर, परन्तु विपरीत प्रकार के बिन्दु-आवेश एक-दूसरे से बहुत कम दूरी पर रखे हों, वैद्युत-द्विध्रुव’ कहलाता है। दोनों आवेशों में से किसी एक आवेश और दोनों आवेशों के बीच की दूरी के गुणनफल को ‘द्विध्रुव’ का ‘वैद्युत-द्विध्रुव आघूर्ण (electric dipole moment) कहते हैं। इसे प्राय: p से प्रदर्शित करते हैं।
चित्र 1.18 में प्रदर्शित वैद्युत-द्विध्रुव का वैद्युत-द्विध्रुव आघूर्ण p = q x 2l


प्रश्न 3.
वैद्युत-द्विध्रुव तथा वैद्युत-द्विध्रुव आघूर्ण से आप क्या समझते हैं? (2017)
या
एकसमान तीव्रता वाले वैद्युत क्षेत्र में वैद्युत द्विध्रुव पर लगने वाले बल-युग्म के आघूर्ण का सूत्र प्राप्त कीजिए। (2012, 17)
या
एकसमान वैद्युत क्षेत्र में एक वैद्युत-द्विध्रुव पर लगने वाले बल-आघूर्ण का व्यंजक प्राप्त कीजिए। इसके आधार पर वैद्युत-द्विध्रुव आघूर्ण की परिभाषा दीजिए। (2014)
उत्तर-
वैद्युत-द्विध्रुव तथा वैद्युत-द्विध्रुव आघूर्ण- वह वैद्युत निकाय (system) जिसमें दो बराबर, परन्तु विपरीत प्रकार के बिन्दु-आवेश एक-दूसरे से बहुत कम दूरी पर रखे हों, “वैद्युत-द्विध्रुव’ कहलाता है। दोनों आवेशों में से किसी एक आवेश और दोनों आवेशों के बीच की दूरी के गुणनफल को ‘द्विध्रुव’ का वैद्युत-द्विध्रुव आघूर्ण (electric dipole moment) कहते हैं। इसे प्रायः p से प्रदर्शित करते हैं।
(i) द्विध्रुव पर शुद्ध स्थानान्तर बल F = qE – qE = 0
(ii) एकसमान वैद्युत-क्षेत्र में रखे वैद्युत-द्विध्रुव पर बल-युग्म–यदि किसी वैद्युत-द्विध्रुव को एकसमान वैद्युत-क्षेत्र (E) में रखा जाए तो उसके आवेशों पर समान और विपरीत बल -qE तथा +qE (अर्थात् एक बल-युग्म) कार्य करने लगता है। यह बल-युग्म द्विध्रुव को क्षेत्र की दिशा में संरेखित (UPBoardSolutions.com) करने का प्रयत्न करता है। इसे प्रत्यानयन बल-युग्म’ कहते हैं। माना एक वैद्युत-द्विध्रुव एकसमान वैद्युत-क्षेत्र (E) में क्षेत्र से 8 कोण बनाते हुए रखा गया है। +q तथा – q पर लगने वाले बराबर एवं विपरीत बले (+qE व -qE) एक बल-युग्म बनाते हैं जो द्विध्रुव को घुमाकर क्षेत्र E की दिशा में लाने का प्रयत्न करता है। इस प्रत्यानयन बल-युग्म का आघूर्ण

प्रश्न 4.
वैद्युत द्विध्रुव की स्थितिज ऊर्जा से आप क्या समझते हैं? एकसमान वैद्युत क्षेत्र में स्थित द्विध्रुव की स्थितिज ऊर्जा का व्यंजक प्राप्त कीजिए, जबकि द्विध्रुव के अक्ष क्षेत्र से 6 कोण बनाएँ।
उत्तर-
वैद्युत द्विध्रुव की स्थितिज ऊर्जा- वैद्युत क्षेत्र में किसी वैद्युत द्विध्रुव की स्थितिज ऊर्जा उस कार्य के बराबर होती है जो कि द्विध्रुव को अनन्त से क्षेत्र के भीतर लाने में करना पड़ता है। एकसमान वैद्युत क्षेत्र में वैद्युत द्विध्रुव की स्थितिज ऊर्जा के लिए व्यंजक- माना कि एक वैद्युत द्विध्रुव AB को अनन्त से किसी एकसमान वैद्युत क्षेत्र E में इस प्रकार लाया जाता है कि द्विध्रुव आघूर्ण p सदैव क्षेत्र B की (UPBoardSolutions.com) दिशा में रहे (चित्र 1.21)। क्षेत्र E के कारण द्विध्रुव के आवेश +q पर एक बल F (= qE) क्षेत्र की दिशा में तथा आवेश -q पर उतना ही बल F (= qE) विपरीत दिशा में कार्य करता है। अतः द्विध्रुव को क्षेत्र में लाने के लिए, आवेश +q पर बाहरी कर्ता द्वारा कार्य किया जाएगा जो धनात्मक होगा, जबकि -q आवेश पर स्वयं क्षेत्र कार्य करेगा, अर्थात् कार्य प्राप्त होगा जो ऋणात्मक होगा। परन्तु चित्र 1.21 से स्पष्ट है कि अनन्त से क्षेत्र के भीतर – q आवेश को लाने में प्राप्त कार्य +q को लाने में किए जाने वाले कार्य से अधिक होगा। बिन्दु A तक लाने में प्राप्त कार्य तथा किया गया कार्य बराबर होंगे। अत: वे एक-दूसरे को निरस्त कर देंगे। अतः द्विध्रुव को स्थिति AB तक लाने में नेट कार्य -q आवेश को A से B तक लाने में प्राप्त कार्य के बराबर होगा, जो ऋणात्मक होगी।


प्रश्न 5.
+3.2 x 10-19 कूलॉम तथा -3.2 x 10-19 कूलॉम के दो बिन्दु आवेश एक-दूसरे से 2.4 x 10-10 मीटर की दूरी पर रखे हैं। यह द्विध्रुव 4 x 105 वोल्ट/मीटर तीव्रता के समांगी वैद्युत-क्षेत्र में स्थित है। ज्ञात कीजिए।
(i) वैद्युत-द्विध्रुव आघूर्ण,
(ii) द्विध्रुव को साम्यावस्था से 180° घुमाने में आवश्यक कार्य तथा
(iii) साम्यावस्था में वैद्युत-द्विध्रुव की स्थितिज ऊर्जा। (2012)
हल-
(i) p. = q x 2l = 3.2 x 10-19 कूलॉम x 2.4 x 10-10 मीटर = 7.68 x 10-29 कूलॉम-मीटर
(ii) वैद्युत-द्विध्रुव को साम्यावस्था अर्थात् वैद्युत-क्षेत्र E की दिशा से θ कोण घुमाने में आवश्यक कार्य
W = pE (1 – cos θ)
यहाँ θ = 180° एवं p = 7.68 x 10-29 कूलॉम-मीटर
E = 4.0 x 105 वोल्ट/मीटर।
W = (7.68 x 10-29) x (4.0 x 105) x (1 – cos 180°)
= (7.68 x 10-29) x (4.0 x 105) x 2 (∵ cos 180° = – 1)
= 6.144 x 10-28 जूल
(iii) वैद्युत-क्षेत्र E में द्विध्रुव को साम्यावस्था से से कोण पर रखे होने पर इसकी स्थितिज ऊर्जा
U = – pE cos θ
जहाँ θ = द्विध्रुव की अक्ष तथा इसकी साम्यावस्था अर्थात् वैद्युत-क्षेत्र की दिशा के बीच स्थित कोण साम्यावस्था में θ = 0°,
अत: U0 = – pE (cos 0° = 1)
यहाँ p = 7.68 x 10-29 कूलॉम-मीटर
E = 4.0 x 105 वोल्ट/मीटर
U0 = – (7.68 x 10-29) x (4.0 x 105) जूल = -3.072 x 10-23 जूल
प्रश्न 6.
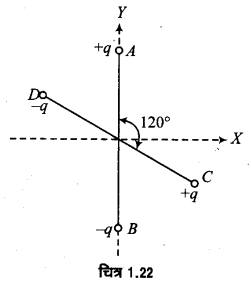
दो एक जैसे वैद्युत-द्विध्रुव AB तथा CD जिनके प्रत्येक के द्विध्रुव आघूर्ण P हैं तथा 120° कोण पर चित्रानुसार रखे हैं। इस संयोजन का परिणामी द्विध्रुव आघूर्ण ज्ञात कीजिए। यदि +x दिशा में एक समरूप वैद्युत क्षेत्र में आरोपित हो तब-संयोजन पर कार्य करने वाले बल-आघूर्ण का मान क्या होगा? (2014)
हल-
माना दोनों आवेशों के बीच की दूरी = 2a
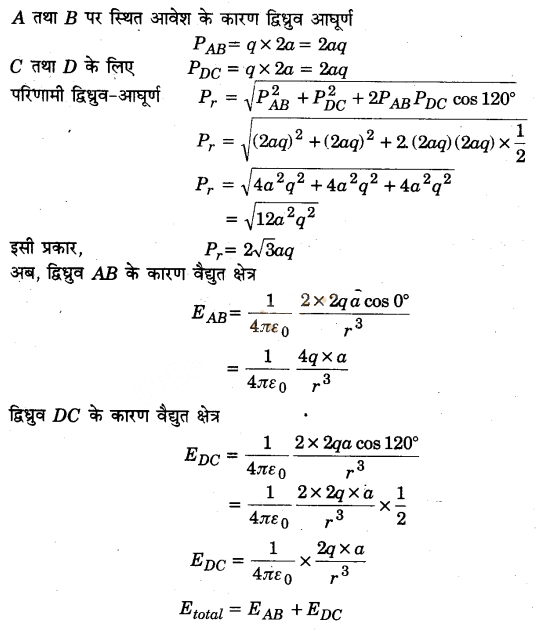
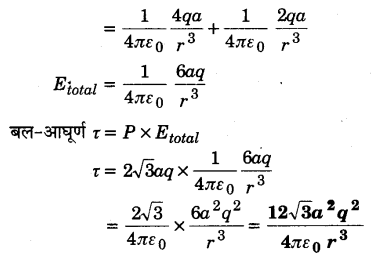
प्रश्न 7.
स्थिर वैद्युत में गौस की प्रमेय क्या है? (2010, 11, 14, 17, 18)
या
सिद्ध कीजिए कि किसी बन्द पृष्ठसे गुजरने वाला वैद्युत-फ्लक्स उस पृष्ठ द्वारा परिबद्ध कुल आवेश q का 1/ε0 गुना होता है, जहाँ ε0 मुक्त आकाश (free space) की वैद्युतशीलता है। (2009, 16)
या
गौस-प्रमेय लिखिए। सिद्ध कीजिए कि किसी बन्द पृष्ठ से गुजरने वाला नेट वैद्युत-फ्लक्स उस पृष्ठ द्वारा परिबद्ध कुल आवेश q का 1/ε0 गुना होता है, जहाँ ε0 मुक्त आकाश की वैद्युतशीलता है।
या
वैद्युत-स्थैतिकी में गौस की प्रमेय लिखिए तथा उसको सिद्ध कीजिए। (2014, 15, 18)
या
स्थिर-विद्युतिकी (वैद्युत-स्थैतिकी) में गौस के नियम का उल्लेख कीजिए। (2014)
उत्तर-
गौस की प्रमेय (Gauss Theorem)- गौस की प्रमेय वैद्युत-क्षेत्र के कारण किसी बन्द पृष्ठ से निर्गत वैद्युत-फ्लक्स तथा उस पृष्ठ से परिबद्ध कुल वैद्युत आवेश के बीच सम्बन्ध व्यक्त करती है। इसके अनुसार–“किसी वैद्युत-क्षेत्र में स्थित बन्द पृष्ठ से निर्गत सम्पूर्ण वैद्युत-फ्लक्स का मान उस पृष्ठ द्वारा परिबद्ध कुल आवेश का (1/ε0) गुना होता है।”


प्रश्न 8.
गौस की प्रमेय से कूलॉम के नियम का निगमन कीजिए। (2018)
या
गौस-प्रमेय की सहायता से दो बिन्दु आवेशों के बीच कार्य करने वाले बल के लिए व्यंजक प्राप्त कीजिए। (2011)
उत्तर-
माना कोई विलगित बिन्दु आवेश +q, वायु या निर्वात् में बिन्दु O पर रखा है। इससे दूरी पर एक बिन्दु P है। इस बिन्दु से गुजरता हुआ q को परिबद्ध किये हुए एक गोलीय (UPBoardSolutions.com) गौसियन-पृष्ठ खींचा गया है। इस बिन्दु पर q के कारण वैद्युत-क्षेत्र की तीव्रता O से P की दिशा में पृष्ठ के लम्बवत् होगी। P के परित: किसी पृष्ठ अवयव के क्षेत्रफल dA का क्षेत्रफल सदिश dA भी E की दिशा में होगा (चित्र 1.24)।
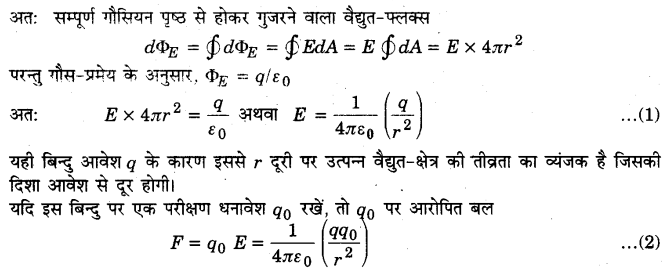
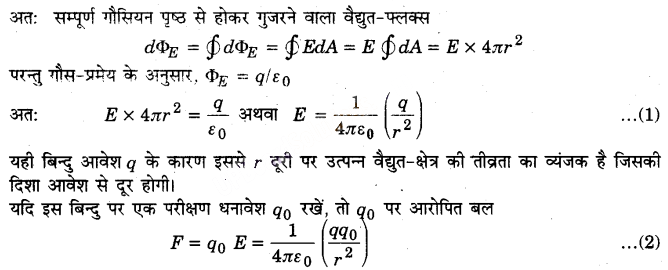
यही कूलॉम का नियम है जो कि गौस-प्रमेय से व्युत्पन्न किया गया है। इस प्रकार, स्थिर विद्युतिकी में कूलॉम का नियम तथा गौस का नियम परस्पर तुल्य हैं। ये दो भौतिक नियम नहीं हैं, बल्कि एक ही नियम है जिसे विभिन्न रूपों में अभिव्यक्त किया गया है।
प्रश्न 9.
गौस के नियम का उपयोग करके एक अनन्त लम्बाई के पतले, सीधे एकसमान आवेशित तार द्वारा उत्पन्न वैद्युत-क्षेत्र की तीव्रता के लिए एक व्यंजक का निगमन कीजिए। (2012)
या
वैद्युत-स्थैतिकी में गौस की प्रमेय बताइए। इसका उपयोग करके एकसमान आवेशित लम्बे तार के निकट वैद्युत-क्षेत्र की तीव्रता के लिए व्यंजक व्युत्पन्न कीजिए। (2011, 13)
या
स्थिर-विद्युतिकी (वैद्युत-स्थैतिकी) का गौस प्रमेय लिंखिए। इसकी सहायता से एक समान रूप से आवेशित अनन्त लम्बाई के सीधे तार के निकट वैद्युत-क्षेत्र की तीव्रता के लिए व्यंजक प्राप्त कीजिए। (2015)
या
अनन्त लम्बाई के समान रूप से आवेशित सीधे तार के निकट वैद्युत क्षेत्र की तीव्रता का व्यंजक गौस के प्रमेय की सहायता से प्राप्त कीजिए। (2017, 18)
उत्तर-
गौस की प्रमेय-दीर्घ उत्तरीय प्रश्न 7 का उत्तर देखिए। अनन्त लम्बाई के आवेशित तार के निकट वैद्युत-क्षेत्र की Y ) , तीव्रता-चित्र 1.25 में एक अनन्त लम्बाई (UPBoardSolutions.com) का चालक तार प्रदर्शित है। जिसके आवेश का रेखीय घनत्व १ कूलॉम प्रति मीटर है। माना यह तार K परावैद्युतांक वाले माध्यम में रखा है। इसकी अक्ष से दूरी पर एक बिन्दु P है जहाँ इस चालक तार के कारण वैद्युत-क्षेत्र की तीव्रता ज्ञात करनी है।
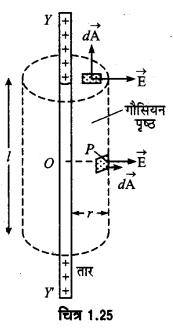
चित्र 1.25 में इस चालक तार के चारों ओर r त्रिज्या का एक ऐसा बेलन दर्शाया गया है जिसकी लम्बाई । है तथा प्रेक्षण बिन्दु P इसके वक्र-पृष्ठ पर है। इस बेलन की अक्ष तथा तार की अक्ष एक ही है। चूंकि तार समान रूप से आवेशित है, अत: इसकी अक्ष से समान दूरी पर स्थित प्रत्येक बिन्दु पर वैद्युत-क्षेत्र की तीव्रता के समान होगी तथा इसकी दिशा अक्ष के लम्बवत् बाहर की ओर होगी। अतः (UPBoardSolutions.com) वैद्युत-क्षेत्र की तीव्रता की दिशी इस बेलन के अनुप्रस्थ काट के चित्र 1.25 समान्तर है। अत: इस बेलन के समतल पृष्ठों से गुजरने वाला वैद्युत-फ्लक्स शून्य होगा क्योंकि इसका क्षेत्रफल वेक्टर A, वेक्टर E के लम्बवत् होगा, इसलिए वैद्युत-फ्लक्स


प्रश्न 10.
गौस के नियम का उपयोग करके एक समान आवेशित अनन्त समतल चादर के कारण विद्युत क्षेत्र ज्ञात कीजिए। (2017)
या
गौस के नियम का प्रयोग करते हुए एक असीमित (अनन्त) विस्तार वाली आवेशित समतल चादर के निकट वैद्युत-क्षेत्र की तीव्रता ज्ञात कीजिए। (2015, 16)
या
वैद्युत स्थैतिकी में गौस-नियम का उल्लेख कीजिए। इस नियम का उपयोग करके अनन्त विस्तार की समतल आवेशित अचालक प्लेट के निकट वैद्युत-क्षेत्र की तीव्रता ज्ञात कीजिए। (2011)
या
वैद्यत स्थैतिकी में गौस की प्रमेय का उल्लेख कीजिए। इसकी सहायता से अनन्त विस्तार की समतल आवेशित प्लेट के निकट वैद्युत क्षेत्र की तीव्रता ज्ञात कीजिए। (2013, 17)
उत्तर-
गौस की प्रमेय (Gauss’ Theorem)- दीर्घ उत्तरीय प्रश्न 7 में देखिए।
अनन्त विस्तार की समतल आवेशित प्लेट के कारण किसी निकट बिन्दु पर वैद्युत-क्षेत्र की तीव्रता- चित्र 1.26 में BCDG एक अनन्त विस्तार की आवेशित समतल प्लेट है, जिसकी मोटाई नगण्य है। इस प्रकार की प्लेट के दोनों पृष्ठों पर समान आवेश होता है। माना इसके प्रत्येक पृष्ठ पर आवेश का पृष्ठ घनत्व 0 है।
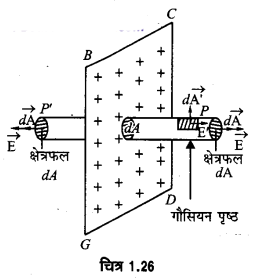
यदि प्लेट धनावेशित है तो इसके कारण वैद्युत-क्षेत्र की तीव्रता प्लेट के लम्बवत् बाहर की ओर होती है। और यदि प्लेट ऋणावेशित है तो तीव्रता प्लेट के लम्बवत् अन्दर की ओर होती है। चित्रे 1.26 में धनावेशित प्लेट दिखायी गयी है।
माना इस प्लेट के निकट बिन्दु P पर वैद्युत-क्षेत्र की तीव्रता ज्ञात करनी है। इसके लिए इसे प्लेट के आर-पार एक बेलनाकार गौसियन पृष्ठ की कल्पना करते हैं जिसकी अनुप्रस्थ काट P के परितः। क्षेत्रफल अवयव dA है जो सीट (प्लेट) के समान्तर है। बेलन के P तथा P’ सिरे प्लेट से (UPBoardSolutions.com) समान दूरी पर हैं। सिरे P पर dA के प्रत्येक बिन्दु पर वैद्युत-क्षेत्र की तीव्रता (E) समान होगी। यह वैद्युत-क्षेत्र की तीव्रता पृष्ठ के लम्बवत् बाहर की ओर होगी। क्षेत्रफल अवयव dA को क्षेत्रफल सदिश dA से प्रदर्शित किया गया है जो E की ही दिशा में होगा। अत: सिरे P पर इस पृष्ठ से गुजरने वाला वैद्युत-फ्लक्स-

प्रश्न 11.
गौस प्रमेय की सहायता से अनन्त विस्तार की समतल आवेशित चालक प्लेट के कारण वैद्युत-क्षेत्र की तीव्रता के सूत्र का निगमन कीजिए। (2012)
उत्तर-
माना अनन्त विस्तार एवं परिमित लघु मोटाई की एक धन-आवेशित ‘समतल चालक प्लेट निर्वात् (अथवा वायु) में स्थित है (चित्र 1.27)। चूँकि प्लेट एक ‘समतल (UPBoardSolutions.com) चालक है, अत: प्लेट को दिया गया सम्पूर्ण आवेश प्लेट के बाह्य पृष्ठों 1 व 2 पर एकसमान रूप से वितरित हो जाता है। प्लेट के भीतर वैद्युत क्षेत्र सर्वत्र शून्य होता है तथा प्लेट के पृष्ठों पर एवं समीपवर्ती बाह्य बिन्दुओं पर वैद्युत क्षेत्र प्लेट के पृष्ठों के लम्बवत् होता है। माना कि प्लेट पर आवेश की पृष्ठ-घनत्व ० है।


धन-आवेशित चालक प्लेट के कारण वैद्युत क्षेत्र की दिशा प्लेट के लम्बवत् तथा प्लेट से परे की ओर को दिष्ट है। यदि प्लेट ऋण-आवेशित हो तब क्षेत्र की दिशा प्लेट के लम्बवत् तथा प्लेट की ओर को दिष्ट होगी। हमने उपरोक्त सूत्र एक समतल आवेशित चालक के लिए प्राप्त किया है। वास्तव (UPBoardSolutions.com) में यह किसी भी आकृति’ के चालक के लिए सत्य है। इस सूत्र से स्पष्ट है कि अनन्त विस्तार के आवेशित चालक के ‘निकट’ किसी बिन्दु पर वैद्युत क्षेत्र की तीव्रता चालक के क्षेत्रफल अथवा चालक से इस बिन्दु की दूरी पर निर्भर नहीं करती। इसका अर्थ है कि चालक के निकट’ सभी बिन्दुओं पर वैद्युत क्षेत्र की तीव्रता समान होती है।
प्रश्न 12.
एकसमान आवेशित गोलीय कोश के कारण उसके पृष्ठ के किसी बिन्दु पर वैद्युत-क्षेत्र की तीव्रता का व्यंजक प्राप्त कीजिए। (2015)
या
एकसमान आवेशित गोलीय कोश के कारण उसके पृष्ठ पर, कोश के बाह्य बिन्दु पर तथा कोश के भीतर वैद्युत-क्षेत्र की तीव्रता का व्यंजक ज्ञात कीजिए।
या
गौस प्रमेय की सहायता से किसी आवेशित गोलीय कोश के बाहर किसी बिन्दु पर वैद्युत-क्षेत्र की तीव्रता ज्ञात कीजिए। (2015, 16, 17)
या
एकसमान आवेशित गोलीय कोश के कारण विद्युत क्षेत्र की तीव्रता का व्यंजक गौस के नियम के आधार पर प्राप्त कीजिए जबकि बिन्दु कोश के
(i) बाहर,
(ii) पृष्ठ पर तथा
(iii) भीतर स्थित है। (2017)
उत्तर-
माना कि त्रिज्या R का एक विलगित (isolated) गोलीय कोश है जिस पर ओवश +qएकसमान रूप से वितरित है। हमें इस कोश के बाहर, कोश के पृष्ठ पर तथा कोश के भीतर वैद्युत-क्षेत्र की तीव्रता ज्ञात करनी है।
बाह्य बिन्दु पर (At an External Point)- माना कि आवेशित कोश के केन्द्र O (चित्र 1.28) से दूरी r पर (r > R) एक बिन्दु P है जिस पर वैद्युत क्षेत्र की (UPBoardSolutions.com) तीव्रता ज्ञात करनी है। इसके लिये, हम बिन्दु P से गुजरने वाला, त्रिज्या F का संकेन्द्री गोलीय पृष्ठ खींचते हैं जिसे गौसियन पृष्ठ’ (Gaussian surface) कहते हैं। आवेश-वितरण की सममिति के कारण, गौसियन पृष्ठ के सभी बिन्दुओं पर वैद्युत-क्षेत्र का परिमाण E समान होगा तथा दिशा बाहर की ओर को त्रिज्यतः (radially outward) होगी।



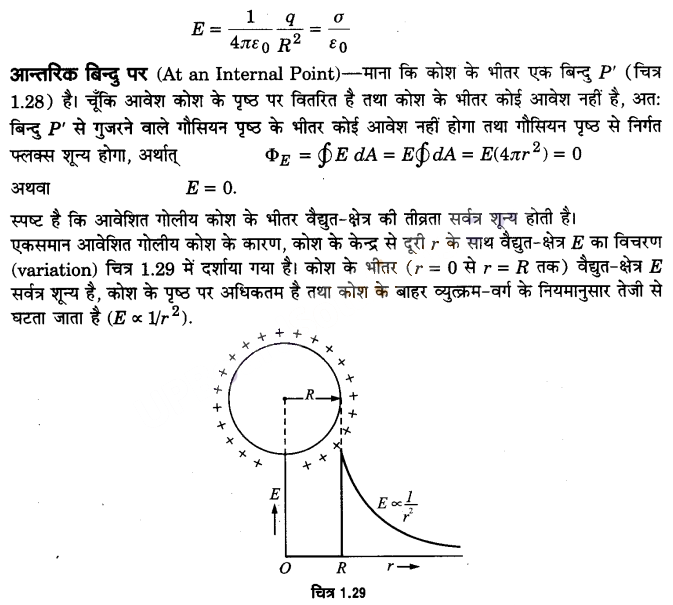
प्रश्न 13.
गौस की प्रमेय बताइए। एकसमान रूप से आवेशित अचालक गोले के कारण किसी बाह्य बिन्दु पर उत्पन्न वैद्युत-क्षेत्र की तीव्रता के लिए व्यंजक प्राप्त कीजिए। (2010, 12)
या
‘R’ त्रिज्या के एकसमान रूप से आवेशित अचालक गोले के केन्द्र से (r < R) दूरी पर वैद्युत-क्षेत्र की तीव्रता का व्यंजक ज्ञात कीजिए। (2012)
उत्तर-
गौस की प्रमेय- दीर्घ उत्तरीय प्रश्न 7 में देखिए।

माना R त्रिज्या का एक विलगित (isolated) अचालक (non-conducting) ठोस गोला है जिसके सम्पूर्ण आयतन में 2 आवेश एकसमान रूप से वितरित है। इसके केन्द्र O से r दूरी पर स्थित बिन्दु P पर इसके कारण उत्पन्न वैद्युत-क्षेत्र की तीव्रता ज्ञात करनी है, जबकि r < R.
यह बिन्दु P गोले के भीतर केन्द्र O से r दूरी पर है। P पर वैद्युत-क्षेत्र की तीव्रता प्राप्त करने के लिए बिन्दु P से गुजरने वाली गोलीय गौसियन पृष्ठ खींचते हैं। P के परित: (UPBoardSolutions.com) गौसियन पृष्ठ के अल्पांश क्षेत्रफल अवयव dA का क्षेत्रीय सदिश dA भी पृष्ठ के लम्बवत् अर्थात् है की दिशा में ही होगा अर्थात् उनके बीच कोण शून्य है। अत: क्षेत्रफल अवयव dA से होकर जाने वाला वैद्युत-फ्लक्स

प्रश्न 14.
एकसमान आवेशित अचालक गोले के भीतर किसी बिन्दु पर गौस प्रमेय की सहायता से वैद्युत-क्षेत्र की तीव्रता का सूत्र स्थापित कीजिए। (2013)
उत्तर-
माना कि बिन्दु P गोले के भीतर केन्द्र0 से दूरी पर है। (चित्र 1.31)।
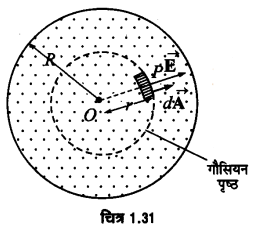
P पर वैद्युत-क्षेत्र की तीव्रता प्राप्त करने के लिए। बिन्दु P से गुजरने वाला गोलीय गौसियन पृष्ठ खींचते हैं। माना आवेशित गोले के कारण P पर उत्पन्न वैद्युत-क्षेत्र की तीव्रता में है। आवेश वितरण की सममिति के कारण गौसियन पृष्ठ के प्रत्येक बिन्दु पर वैद्युत-क्षेत्र की तीव्रता का परिमाण E समान (UPBoardSolutions.com) होगा तथा दिशा पृष्ठ के लम्बवत् होगी। P के परित: गौसियन पृष्ठ के अल्पांश क्षेत्रफल अवयव dA को चित्र 1.31 क्षेत्रीय सदिश dA भी पृष्ठ के लम्बवत् अर्थात् है की दिशा में ही होगी अर्थात् उनके बीच कोण शून्य है। अत: क्षेत्रफल अवयव dA से होकर जाने वाला वैद्युत फ्लक्स

