UP Board Solutions for Class 11 Physics Chapter 9 Mechanical Properties Of Solids (ठोसों के यान्त्रिक गुण)

अभ्यास के अन्तर्गत दिए गए प्रश्नोत्तर

प्रश्न 1.
4.7 m लम्बे व 3.0 x 10^-5 m² अनुप्रस्थ काट के स्टील के तार तथा 3.5 m लम्बे व 40 x 10^-5m² अनुप्रस्थ काट के ताँबे के तार पर दिए गए समान परिमाण के भारों को लटकाने पर उनकी लम्बाइयों में समान वृद्धि होती है। स्टील तथा ताँबे के यंग-प्रत्यास्थता गुणांकों में क्या अनुपात है?
हल-
यंग-प्रत्यास्थता गुणांक
यहाँ दोनों तारों के लिए लटकाया गया भार F = Mg तथा लम्बाई में वृद्धि l समान है, अतः Y∝(L/A)

प्रश्न 2.
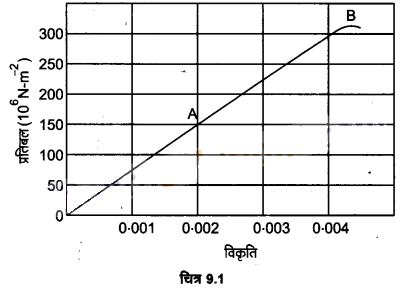
चित्र-9.1 में किसी दिए गए पदार्थ के लिए प्रतिबल-विकृति वक्र दर्शाया गया है। इस पदार्थ के लिए
(a) यंग-प्रत्यास्थता गुणांक, तथा
(b) सन्निकट पराभव सामर्थ्य क्या है?

हल-
(a) ग्राफ के सरल रेखीय भाग में बिन्दु A के संगत
अनुदैर्ध्य प्रतिबल = 150×10⁶ न्यूटन/मी
तथा अनुदैर्घ्य विकृति = 0.002
∴ यंग-प्रत्यास्थता गुणांक

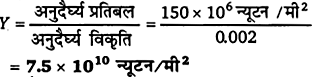
(b) पराभव बिन्दु लगभग B है।
अत: इसके संगत पदार्थ की पराभव सामर्थ्य = 300×10⁶ न्यूटन/मीटर
= 300×10⁸ न्यूटन/मी

प्रश्न 3.
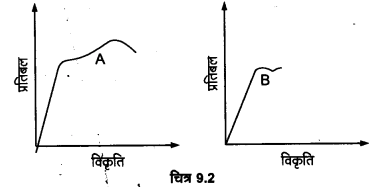
दो पदार्थों A और B के लिए प्रतिबल-विकृति ग्राफ चित्र-9.2 में दर्शाए गए हैं।
| इन ग्राफों को एक ही पैमाना मानकर खींचा गया है।
(a) किस पदार्थ का यंग प्रत्यास्थता गुणांक अधिक है?
(b) दोनों पदार्थों में कौन अधिक मजबूत है?

उत्तर-
(a) ∵ पदार्थ A के ग्राफ का ढाल दूसरे ग्राफ की तुलना में अधिक है; अतः पदार्थ A का यंग गुणांक अधिक है।
(b) दोनों ग्राफों पर पराभव बिन्दुओं की ऊँचाई लगभग बराबर है परन्तु पदार्थ A के ग्राफ में पदार्थ B की तुलना में प्लास्टिक क्षेत्र अधिक सुस्पष्ट है; अतः पदार्थ A अधिक मजबूत है।

प्रश्न 4.
निम्नलिखित दो कथनों को ध्यान से पढिए और कारण सहित बताइए कि वे सत्य हैं या असत्य
(a) इस्पात की अपेक्षा रबड़ का यंग गुणांक अधिक है;
(b) किसी कुण्डली का तनन उसके अपरूपण गुणांक से निर्धारित होता है।
उत्तर-
(a) असत्य, रबड़ तथा इस्पात के बने एक जैसे तारों में समान विकृति उत्पन्न करने के लिए इस्पात के तार में रबड़ के तार की अपेक्षा अधिक प्रतिबल उत्पन्न होता है, इससे स्पष्ट है कि इस्पात का यंग गुणांक रबड़ की अपेक्षा अधिक है।
(b) सत्य, जब हम किसी कुण्डली (स्प्रिग) को खींचते हैं तो न तो स्प्रिंग निर्माण में लगे तार की लम्बाई में कोई परिवर्तन होता है और न ही उसके आयतन में। केवल स्प्रिंग का रूप बदल जाता है; अतः स्प्रिंग का तनन उसके अपरूपण गुणांक द्वारा निर्धारित होता है।

प्रश्न 5.
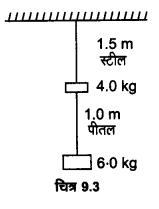
0.25 cm व्यास के दो तार, जिनमें एक इस्पात का तथा दूसरा पीतल का है, चित्र-9.3 के अनुसार भारित हैं। बिना भार लटकाए इस्पात तथा पीतल के तारों की लम्बाइयाँ क्रमशः स्टील 1.5 m तथा 1.0m हैं। यदि इस्पात तथा पीतल के यंग गुणांक क्रमशः 20 x 10¹¹ Pa तथा 0.91×10¹¹ Pa हों तो इस्पात तथा पीतल के तारों में विस्तार की गणना कीजिए।

हल-
यहाँ स्टील के तार के लिए
त्रिज्या r1 = (0.25/2) सेमी = 0.125 सेमी
= 0.125 x 10^-2 मी

प्रश्न 6.
ऐलुमिनियम के किसी घन के किनारे 10 cm लम्बे हैं। इसकी एक फलक किसी ऊर्ध्वाधर दीवार से कसकर जड़ी हुई है। इस घन के सम्मुख फलक से 100 kg का एक द्रव्यमान जोड़ दिया गया है। ऐलुमिनियम का अपरूपण गुणांक 25 GPa है। इस फलक का ऊध्र्वाधर विस्थापन कितना होगा?
हल-
दिया है : अपरूपण गुणांक G =25 GPa = 25 x 10⁹ Nm^-2

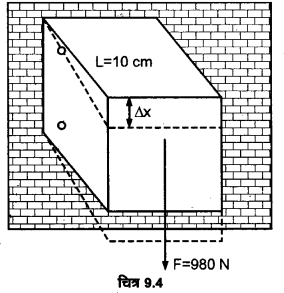
बल-आरोपित फलक का क्षेत्रफल A = 10 cm x 10 cm = 100 x 10^-4 m²

प्रश्न 7.
मृदु इस्पात के चार समरूप खोखले बेलनाकार स्तम्भ 50,000 kg द्रव्यमान के किसी बड़े ढाँचे को आधार दिए हुए हैं। प्रत्येक स्तम्भ की भीतरी तथा बाहरी त्रिज्याएँ क्रमशः 30 तथा 60 cm हैं। भार वितरण को एकसमान मानते हुए प्रत्येक स्तम्भ की सम्पीडन विकृति की गणना कीजिए।
हल-
दिया है : बाहरी त्रिज्या R_ext = 60 cm = 0.6 m
भीतरी त्रिज्या R_int =30 cm = 0.3 m
∴ प्रत्येक स्तम्भ का अनुप्रस्थ क्षेत्रफल

प्रश्न 8.
ताँबे का एक टुकड़ा, जिसका अनुप्रस्थ परिच्छेद 15.2 mm x 19.1 mm का है, 44,500 N बल के तनाव से खींचा जाता है, जिससे केवल प्रत्यास्थ विरूपण उत्पन्न हो। उत्पन्न विकृति की गणना कीजिए।
हल-
विरूपण विकृति से संगत प्रत्यास्थता गुणांक अपरूपण गुणांक (दृढ़ता गुणांक η होता है जो यहाँ 4.20 x 10¹⁰ Pa) दिया है।
ताँबे के टुकड़े का अनुप्रस्थ-परिच्छेद
A = (15.2 x 10^-3 मी) x (19.1 x 10^-3 मी)
=290.32 x 10^-6 मी² = 2.9 x 10^-4 मी²
विरूपक बल F =44500 न्यूटन = 4.45 x 10⁴ न्यूटन

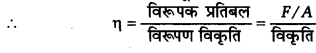
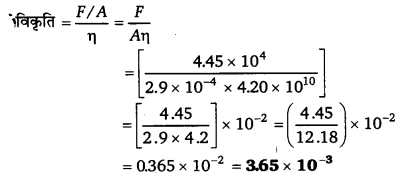
प्रश्न 9.
1.5 cm त्रिज्या का एक इस्पात का केबिल भार उठाने के लिए इस्तेमाल किया जाता है। | यदि इस्पात के लिए अधिकतम अनुज्ञेय प्रतिबल 10⁸ Nm^-2 है तो उस अधिकतम भार की गणना कीजिए जिसे केबिल उठा सकता है।
हल-
केबिल के अनुप्रस्थ-परिच्छेद का क्षेत्रफल ।
A = πr² = 3.14 x (1.5 x 10^-2 मी )² = 7.065 x 10^-4 मी²
। अधिकतम अनुज्ञेय प्रतिबल = 10⁸ न्यूटन/मीटर²
∴ बल F = (F/A) x A = प्रतिबल x अनुप्रस्थ-काट का क्षेत्रफल
∴ केबिल द्वारा उठाया जा सकने वाला अधिकतम भार ।
= अनुज्ञेय प्रतिबल x अनुप्रस्थ-काट को क्षेत्रफल
= (10⁸ न्यूटन /मी²) x (7.065 x 10^-4 मी²)
= 7.065 x 10⁴ न्यूटन = 7.07 x 10⁴ न्यूटन

प्रश्न 10.
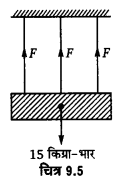
15 kg द्रव्यमान की एक दृढ़ पट्टी को तीन तारों, जिनमें से प्रत्येक की लम्बाई 2 m है, से सममित लटकाया गया है। सिरों के दोनों तार ताँबे के हैं तथा बीच वाली तार लोहे का है। तारों के व्यासों के अनुपात ज्ञात कीजिए जबकि प्रत्येक पर तनाव उतना ही रहता है।


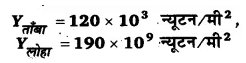
हल-
प्रत्येक तार द्वारा सम्भाला जाने वाला भार

प्रश्न 11.
एक मीटर अतानित लम्बाई के इस्पात के तार के एक सिरे से 14.5 kg का द्रव्यमान बाँध कर उसे एक ऊर्ध्वाधर वृत्त में घुमाया जाता है, वृत्त की तली पर उसका कोणीय वेग 2 rev/s है। तार के अनुप्रस्थ परिच्छेद का क्षेत्रफल 0.065cm² है। तार में विस्तार की • गणना कीजिए जब द्रव्यमान अपने पथ के निम्नतम बिन्दु पर है। (इस्पात के लिए Y =2×10¹¹ न्यूटन/मी²)
हल-
ऊध्र्वाधर वृत्त के निम्नतम बिन्दु पर
F – mg = mrω²
डोरी में तनाव बल F = mrω² + mg
F = [14.5 x 1.0 x (2.0)² + 14.5 x 9.8] न्यूटन
= [58.0 + 142.1] न्यूटन = 200.1 न्यूटन
तथा L = 1.00 मी, अनुप्रस्थ-काट A = 0.065 सेमी² = 0.065 x 10^-4 मी² तथा
Y =2 x 10¹¹ न्यूटन/मी²
सूत्र

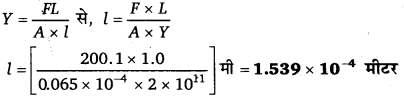
प्रश्न 12.
नीचे दिए गए आँकड़ों से जल के आयतन प्रत्यास्थता गुणांक की गणना कीजिए; प्रारम्भिक आयतन = 100.0, दाब में वृद्धि = 100.0 atm (1 atm =1.013 x 10⁵ Pa), अन्तिम आयतन = 100.5 L नियत ताप पर जल तथा वायु के आयतन प्रत्यास्थता गुणांकों की तुलना कीजिए। सरल शब्दों में समझाइए कि यह अनुपात इतना अधिक क्यों है?
हल-
यहाँ प्रारम्भिक आयतन V = 100.0 लीटर
अन्तिम आयतन (V – υ) = 100.5 लीटर
आयतन में कमी υ = (V – υ) – (V) = 100 लीटर – 100.5 लीटर = – 0.5 लीटर
दाब में वृद्धि p = 100 वायुमण्डलीय दाब ।
= 100 x 1.013 x 10⁵ न्यूटन/मी²
= 1.013 x 10⁷ न्यूटन/मी
आयतन प्रत्यास्थता गुणांक

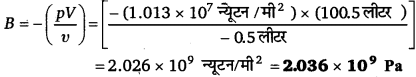
हम जानते हैं कि STP पर वायु का आयतन प्रत्यास्थता गुणांक 1 x 10⁵ Pa है, अतः जल का आयतन । प्रत्यास्थता गुणांक वायु के आयतन प्रत्यास्थता गुणांक से अधिक है। इसका कारण है कि समान दाब द्वारा जल के आयतन में होने वाली कमी, वायु के आयतन में होने वाली कमी की तुलना में नगण्य है।

प्रश्न 13.
जल का घनत्व उस गंहराई पर, जहाँ दाब 80.0 atm हो, कितना होगा? दिया गया है कि | पृष्ठ पर जल का घनत्व 103 x 10 kg³ m^-3, जल की सम्पीड्यता 45.8 x 10^-11 Pa^-1(1 Pa = 1Nm^-2)
हल-
यहाँ पृष्ठ से गहराई तक जाने पर दाब परिवर्तन p = (80.0-1.0) वायुमण्डल = 79वायुमण्डल अर्थात् ।
p = 79 x 1.013 x 10⁵ न्यूटन/मी²
= 80.027 x 10⁵ न्यूटन/मी²
जहाँ जल की संपीड्यता K = 45.8 x 10^-11 Pa^-1
जल को आयतन प्रत्यास्थता गुणांक

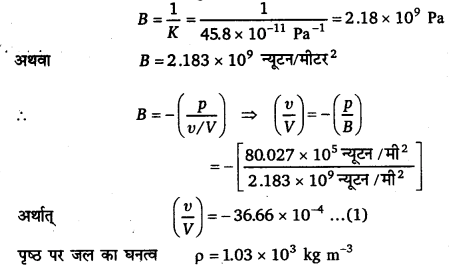
पृष्ठ पर जल का घनत्व ρ = 1.03 x 10³ kg m^-3।
माना ρ’ किसी दी गई गहराई पर जल का घनत्व है। यदि V तथा  V’ जल के निश्चित द्रव्यमान M के पृष्ठ तथा दी गई गहराई के आयतन हैं तो

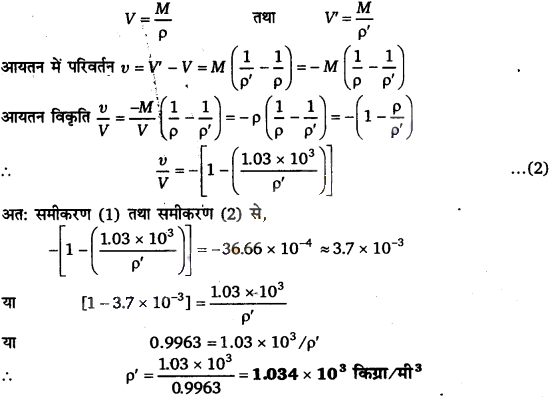
प्रश्न 14.
काँच के स्लेब पर 10 atm का जलीय दाब लगाने पर उसके आयतन में भिन्नात्मक अन्तर की गणना कीजिए।
हल-
यहाँ दाब-परिवर्तन p = 10 वायुमण्डलीय दाब
= 10 x 1.013 x 10⁵ Pa = 1.013 x 10⁶ Pa
आयतन प्रत्यास्थता गुणांक B = 37 x 10⁹ Pa
आयतन प्रत्यास्थता गुणांक

आयतन में भिन्नात्मक परिवर्त
यहाँ (-) चिह्न आयतन में कमी का प्रतीक है।

प्रश्न 15.
ताँबे के एक ठोस धन का एक किनारा 10 cm का है। इस पर 7.0 x 10⁶ Pa.का.जलीय दाब लगाने पर इसके आयतन में संकुचन निकालिए।
हल-
आयतन विकृति

परन्तु घन के किनारे की लम्बाई a = 10 सेमी = 0.10 मी
घन का आयतन 20 = a3 = (0.10 मी) 3 = 10-3 मी
अतः आयतन में परिवर्तन ) = आयतन विकृति x आयतन
= – 5×10-5 x 10-3 मी
=-5×10-8 x 106 सेमी
=-0.05 सेमी
(-) चिह्न आयतन में संकुचन का प्रतीक है।

प्रश्न 16.
1 लीटर जल पर दाब में कितना अन्तर किया जाए कि वह 0.10% से सम्पीडित हो जाए?
हल-
यहाँ आयतन में प्रतिशत संकुचन = – 0.10

अर्थात् दाब 2.2 x 10⁶ Pa बढ़ाया जाये।

अतिरिक्त अभ्यास

प्रश्न 17.
हीरे के एकल क्रिस्टलों से बनी निहाइयों, जिनकी आकृति चित्र-9.6 में दिखाई गई है, का उपयोग अति उच्च दाब के अन्तर्गत द्रव्यों के व्यवहार की जाँच के लिए किया जाता है। निहाई के संकीर्ण सिरों पर सपाट फलकों का व्यास 0.50 mm है। यदि निहाई के चौड़े सिरों पर 50,000 N का बल लगा हो तो उसकी नोंक पर दाब ज्ञात कीजिए।

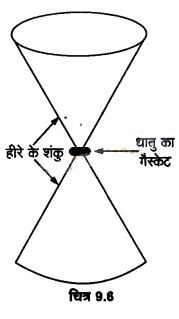
हल-
सपाट फलक की त्रिज्या R = 0.25 mm = 2.5 x 10^-4 m हीरे के शंकु ।
फलक का क्षेत्रफल A = πR²
=3.14 x (2.5 x 10^-4m)²
=196 x 10^-8m
जबकि आरोपित बल F = 50,000N
नोंक पर दाब P
=2.55 x 10¹¹ Pa

प्रश्न 18.
1.05 mलम्बाई तथा नगण्य द्रव्यमान की एक छड़ को बराबर लम्बाई के दो तारों, एक इस्पात : का (तार A) तथा दूसरा ऐलुमिनियम का तार (तार B) द्वारा सिरों से लटका दिया गया है, जैसा कि चित्र-9.7 में दिखाया गया है। A तथा B के तारों के अनुप्रस्थ परिच्छेद के क्षेत्रफल क्रमशः 1.0 mm² और 2.0 mm हैं। छड़ के किस बिन्दु से एक द्रव्यमान m को लटका दिया जाए ताकि इस्पात तथा ऐलुमिनियम के तारों में (a) समान प्रतिबल, तथा (b) समान विकृति उत्पन्न हो?

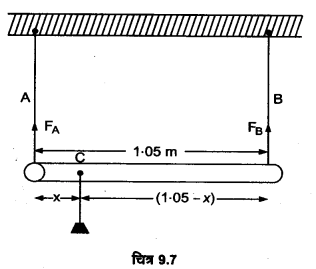
हल-
तारों के अनुप्रस्थ क्षेत्रफल
A_A = 1.0 mm², AB =2.0 mm²
Y_A = 2.0 x 10¹¹ Nm^-2,
Y_B = 0.7 x 10¹¹ Nm^-2
माना द्रव्यमान को तार A वाले सिरे से, x दूरी पर बिन्दु C से लटकाया गया है, तब इसकी दूसरे ‘सिरे से दूरी (1.05 – x) m होगी।
माना इस भार के कारण तारों में F_A तथा F_B तनाव बले उत्पन्न होते हैं।
बिन्दु C के परितः आघूर्ण लेने पर,
F_A .x = F_B (1.05-x) ….(1)
(a) तारों में समान प्रतिबल उत्पन्न होता है; अत:


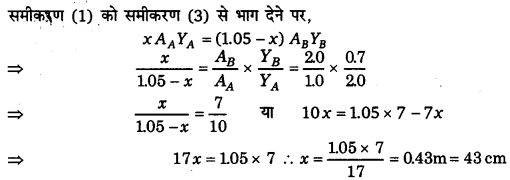
अत: द्रव्यमान को तार A वाले सिरे से 43 cm की दूरी पर लटकाना चाहिए।

प्रश्न 19.
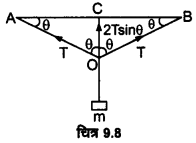
मृदु इस्पात के एक तार, जिसकी लम्बाई 1.0 m तथा अनुप्रस्थ परिच्छेद का क्षेत्रफल – 0.50 x 10^-2 cm है, को दो खम्भों के बीच क्षैतिज दिशा में प्रत्यास्थ सीमा के अन्दर ही तनित किया जाता है। तार के मध्य बिन्दु से 100g का एक द्रव्यमान लटका दिया जाता है। मध्य बिन्दु पर अवनमन की गणना कीजिए।
हल-
दिया है : तार की लम्बाई L = 1.0 m,
अनुप्रस्थ परिच्छेद का क्षेत्रफल A = 0.50 x 10^-2 cm² = 5 x 10^-7 m²
m = 100 g = 0.1 kg, Y = 2.0 x 10¹¹ Nm^-2
माना सन्तुलन की स्थिति में तार के दोनों भागों का क्षैतिज से – झुकाव θ है तथा तार के दोनों भागों में समान तनाव T है। सन्तुलन की स्थिति में,
2T sin θ = mg …(1)
(C तार का मध्य बिन्दु है जो भार लटकाने पर बिन्दु O तक विस्थापित हो जाता है।)

प्रश्न 20.
धातु के दो पहियों के सिरों को चार रिवेट से आपस में जोड़ दिया जाता है। प्रत्येक रिवेट का व्यास 6 मिमी है। यदि रिवेट का अपरुपण प्रतिबल 6.9 x 10⁷ Pa से अधिक नहीं बढ़ना | हो तो रिवेट की हुई पट्टी द्वारा आरोपित तनाव का अधिकतम मान कितना होगा? मान लीजिए कि प्रत्येक रिवेट एक-चौथाई भार वहन कर सकता है।
हल-
दिया है, प्रत्येक रिवेट का व्यास = 6 मिमी ।
∴ त्रिज्या r = व्यास/2 = 6 मिमी/2 = 3 मिमी = 3 x 10^-3 मी
अतः रिवेट का अनुप्रस्थ क्षेत्रफल ।
A = πr² = 3.14 x (3 x 10^-3 मी)²
= 28.26 x 10^-6 मी²
भंजक प्रतिबल = रिवेट द्वारा सहन किये जा सकने वाला अधिक अपरूपण प्रतिबल
= 6.9 x 10⁷ Pa = 6.9 x 10⁷ न्यूटन/मीटर²
प्रत्येक रिवेट द्वारा सहन किया जा सकने वाला अधिकतम तनाव = भंजक प्रतिबल x A
= (6.9 x 10⁷ न्यूटन/मी²) x (28.26 x 10^-6 मी²)
= 1.949 x 10³ न्यूटन ≈ 1.95 x 10’न्यूटन
चूँकि पट्टी में चार रिवेट लगी हैं। अत: पट्टी द्वारा आरोपित अधिकतम तनाव
= 4 x 1.95 x 10³ न्यूटन = 7.8 x 10³ न्यूटन

प्रश्न 21.
प्रशांत महासागर में स्थित मैरियाना नामक खाई एक स्थान पर पानी की सतह से 11 km नीचे चली जाती है और उस खाई में नीचे तक 0.32 m³ आयतन का इस्पात का एक गोला गिराया जाता है तो गोले के आयतन में परिवर्तन की गणना करें। खाई के तल पर जल का दाब 1.1 x 10⁸ Pa है और इस्पात का आयतन गुणांक 160 G Pa है।
हल-
यहाँ दाब-परिवर्तन
p = खाई की तली पर दाब = 1.1 x 10⁸ Pa
इस्पात का आयतन प्रत्यास्थता गुणांक
B = 160 G Pa = 160 x 10⁹ Pa = 1.6 x 10¹¹ Pa
गोले का आयतन = V = 0.32 मी³
आयतन प्रत्यास्थता गुणांक

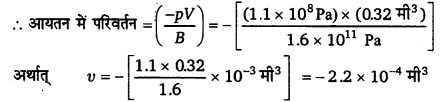
(-) चिह्न आयतन में कमी का प्रतीक है। अर्थात् आयतन में 2.2 x 10^-4 मी³ की कमी होगी।

परीक्षोपयोगी प्रश्नोत्तर

बहुविकल्पीय प्रश्न

प्रश्न 1.
प्रत्यास्थता गुणांक का मात्रक है|
(i) किग्रा/मीटर²-सेकण्ड
(ii) किग्रा/मीटर-सेकण्ड²
(iii) किग्री/मीटर²-सेकण्ड²
(iv) किग्रा/मीटर³-सेकण्ड²
उत्तर-
(ii) किग्रा/मीटर-सेकण्ड²

प्रश्न 2.
दृढ़ता गुणांक (प्रत्यास्थता गुणांक) का विमीय सूत्र है
(i) ML^-1T^-2
(ii) ML^-2T³
(ii) MLT^-2
(iv) ML^-1T¹
उत्तर-
(i) ML^-1T^-2

प्रश्न 3.
ताप बढ़ाने पर यंग-प्रत्यास्थता गुणांक का मान
(i) बढ़ता है।
(ii) घटता है।
(iii) अपरिवर्तित रहता है।
(iv) असामान्य रूप से घटता तथा बढ़ता है।
उत्तर-
(ii) घटता है।

प्रश्न 4.
एक तार से भारmg लटकाने पर तार की लम्बाई में वृद्धि हो जाती है। इस प्रक्रिया में किया गया कार्य है।
(i) mgl
(ii) mgl
(iii) 2mgl
(iv) शून्य
उत्तर-
(i) mgl

प्रश्न 5.
एक धातु के तार की लम्बाई , जिसका यंग प्रत्यास्थता गुणांक है, में वृद्धि होती है, जब इस पर कुछ भार लगाया जाता है। तार के एकांक आयतन में संचित स्थितिज ऊर्जा है।

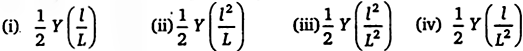
उत्तर-
(iii)

प्रश्न 6.
यदि एक तार को खींचकर दोगुना कर दिया जाए तो उसका यंग प्रत्यास्थता गुणांक हो जायेगा
(i) आधा
(ii) समाने
(ii) दोगुना
(iv) चार गुना
उत्तर-
(ii) समान

प्रश्न 7.
पूर्णतया दृढ़ वस्तु के लिए यंग प्रत्यास्थता गुणांक का मान होता है।
(i) शून्य।
(ii) अनन्त
(iii) 1
(iv) 100
उत्तर-
(ii) अनन्त

प्रश्न 8.
किसी खींचे हुए तार की प्रति एकांक आयतन की स्थितिज ऊर्जा होती है।

उत्तर-
(iii) किसी खींचे हुए तार की प्रति एकांक आयतन की स्थितिज ऊर्जा
= x यंग प्रत्यास्थता गुणांक x विकृति²

प्रश्न 9.
यदि प्रतिबल sहै तथा तार के पदार्थ का यंग गुणांक ४ है तो तार को खींचने पर उसके प्रति एकांक आयतन में संचित ऊर्जा
(i)
(ii)
(iii)
(iv)
उत्तर-
(i) प्रति एकांक आयतन में संचित ऊर्जा =

प्रश्न 10.
आयतन प्रत्यास्थता गुणांक का व्युत्क्रम होता है।
(i) यंग प्रत्यास्थता गुणांक
(ii) दृढ़ता गुणांक
(iii) सम्पीड्यता ।
(iv) विकृति
उत्तर-
(iii) आयतन प्रत्यास्थता गुणांक का व्युत्क्रम सम्पीड्यता होता है।

प्रश्न 11.
पॉयसन अनुपात होता है।
(i) अनुदैर्ध्य प्रतिबल/पाश्विक विकृति
(ii) पाश्विक विकृति/अनुदैर्घ्य विकृति
(iii) अनुदैर्घ्य विकृति/पाश्विक विकृति
(iv) अनुदैर्ध्य प्रतिबल/अनुदैर्ध्य विकृति
उत्तर-
(ii) पॉयसन अनुपात = पाश्विक विकृति/अनुदैर्ध्य विकृति

प्रश्न 12.
प्रत्यास्थता में पॉयसन अनुपात का मान होता है।
(i) से अधिक
(ii) -1 से कम
(iii) -1 और के बीच
(iv) उपर्युक्त में से कोई नहीं
उत्तर-
(iii) प्रत्यास्थता में पॉयसन अनुपात का मान -1 और के बीच होता है।

प्रश्न 13.
Y,η और B में सम्बन्ध होता है|
(i) Y = ηB
(ii) η = YB
(iii)
(iv)
उत्तर-
(iii) Y, η और B में सम्बन्ध

अतिलघु उत्तरीय प्रश्न

प्रश्न 1.
प्रत्यास्थता की सीमा से आप क्या समझते हैं?
उत्तर-
किसी वस्तु पर लगाये गये विरूपक बल की उस अधिकतम सीमा को जिसके अन्तर्गत वस्तु के । पदार्थ में प्रत्यास्थता का गुण विद्यमान रहता है, उस पदार्थ की प्रत्यास्थता की सीमा कहते हैं।

प्रश्न 2.
प्रतिबल की परिभाषा तथा मात्रक लिखिए।
उत्तर-
साम्यावस्था में वस्तु की अनुप्रस्थ-काट के एकांक क्षेत्रफल पर कार्य करने वाले आन्तरिक प्रतिक्रिया बल को प्रतिबल कहते हैं। इसका मात्रक न्यूटन/मीटर है।

प्रश्न 3.
प्रतिबल एवं दाब में अन्तर बताइए।
उत्तर-
किसी वस्तु की अनुप्रस्थ-काट के एकांक क्षेत्रफल पर कार्य करने वाले आन्तरिक प्रतिक्रिया बल को प्रतिबल कहते हैं जबकि किसी पृष्ठ के प्रति एकांक क्षेत्रफल पर कार्य करने वाले अभिलम्बवत् बल को दाब कहते हैं।

प्रश्न 4.
भंजक प्रतिबल से आप क्या समझते हैं।
उत्तर-
जब विरूपक बल का मान प्रत्यास्थता की सीमा से बाहर हो जाता है तो तार की लम्बाई में वृद्धि सदैव के लिए हो जाती है। विरूपक बेल और अधिक बढ़ाने पर एक ऐसी स्थिति उत्पन्न हो जाती है कि विरूपक बल का मान एक निश्चित मान से अधिक हो जाता है और तार टूट जाता है। विरूपक बले को वह मान जिस पर तार टूट जाता है, भंजक बल (breaking force) कहलाता है। अत: तार के अनुप्रस्थ काट के एकांक क्षेत्रफल पर लगने वाला वह बल जिस पर तार टूट जाता है, भंजक प्रतिबल (breaking stress) कहलाता है।

प्रश्न 5.
विकृति से क्या तात्पर्य है?
उत्तर-
विरूपक बल के कारण किसी वस्तु की इकाई विमा में होने वाले परिवर्तन को विकृति कहते हैं। इसका कोई मात्रक नहीं होता इसीलिए यह एक विमाहीन राशि है।

प्रश्न 6.
दृढ़ता गुणांक की परिभाषा लिखिए तथा इसका मात्रक भी लिखिए।
उत्तर-
दृढ़ता गुणांक-प्रत्यास्थता की सीमा के अन्दर, अपरूपक प्रतिबल तथा अपरूपण विकृति के अनुपात को ठोस वस्तु के पदार्थ का दृढ़ता गुणांक (modulus of rigidity) कहते हैं। इसे 1 से प्रदर्शित किया जाता है। इसका मात्रक न्यूटन/मीटर² है।

प्रश्न 7.
काँच, ताँबा, इस्पात तथा रबर को प्रत्यास्थता-गुणांकों के बढ़ते क्रम में लिखिए।
उत्तर-
रबर, काँच, ताँबा, इस्पात।

प्रश्न 8. किसी तार को खींचने में कार्य क्यों करना पड़ता है? इस कार्य का क्या होता है?
उत्तर-
तार को खींचने में अन्तरा-परमाणुक बलों के विरुद्ध कार्य करना पड़ता है। यह कार्य खिंचे तार में प्रत्यास्थ स्थितिज ऊर्जा के रूप में संचित हो जाता है।

प्रश्न 9.
एक तार की लम्बाई काटकर आधी कर दी जाती है।
(i) दिए गए भार के अन्तर्गत इसकी लम्बाई में वृद्धि पर क्या प्रभाव पड़ेगा?
(ii) अधिकतम भार पर, जो वह वहन करती है, क्या प्रभाव पड़ता है?
उत्तर-
(i) लम्बाई में वृद्धि आधी रह जायेगी,
(ii) कोई प्रभाव नहीं, क्योंकि विकृति ΔL/L उतनी ही रहेगी।

प्रश्न 10.
यदि किसी तार के लिए ब्रेकिंग बल F हो, तो (i) इसी आकार के दो समान्तर तारों के लिए तथा (ii) इस तार से दोगुने मोटे तार के लिए ब्रेकिंग बल क्या होंगे?
उत्तर-
(i) 2F क्योंकि कुल परिच्छेद-क्षेत्रफल दोगुना होगा। (ii) 4F क्योंकि दोगुने मोटे तार का परिच्छेद-क्षेत्रफल चार गुना होगा।

प्रश्न 11.
इस्पात तथा ताँबे की समान आकारों की स्प्रिंगों को समान वृद्धि तक खींचा जाता है। किस पर अधिक कार्य करना पड़ेगा?
उत्तर-
इस्पात का यंग-प्रत्यास्थता गुणांक (Y) ताँबे की तुलना में अधिक होता है। अतः यदि स्प्रिंग समान आकार की है (A, L बराबर हैं), तो बराबर-बराबर खींचने (वृद्धि x) के लिए इस्पात की स्प्रिंग पर अधिक कार्य करना पड़ेगा।
चूंकि

प्रश्न 12.
किसी धातु के परमाणुओं के बीच की औसत दूरी 30 Å है। यदि धातु का यंग-प्रत्यास्थता गुणांक 1.8 x 10¹¹ न्यूटन/मीटर हो, तो उसका अन्तरा-परमाणुक बल-नियतांक ज्ञात कीजिए।
हल-
k = 1.8 x 10¹¹ x 3.0 x 10^-10 = 54 न्यूटन/मी

प्रश्न 13.
1 वर्ग सेमी अनुप्रस्थ परिच्छेद के प्रत्यास्थ तार से 1.0 किग्रा द्रव्यमान का पिण्ड लटकाने पर तार में उत्पन्न प्रतिबल का मान ज्ञात कीजिए।
हल-
तार का क्षेत्रफल A = 1 वर्ग सेमी = 1 x 10-4 वर्ग मी,
द्रव्यमान m = 1.0 किग्रा ।
प्रतिबल = 9.8 x 10° न्यूटन/मी

प्रश्न 14.
एक तार में 2 x 10^-4 रेखीय विकृति उत्पन्न करने पर उसमें संचित एकांक आयतन की ऊर्जा ज्ञात कीजिए। तार के पदार्थ का यंग प्रत्यास्थता गुणांक 12 x 10¹¹ न्यूटन/मी² हैं।
हल-
तार में विकृति = 2 x 10^-4
तथा तार के पदार्थ का यंग प्रत्यास्थता गुणांक = 1.2 x 10¹¹ न्यूटन/मी²
तार में संचित एकांक आयतन की ऊर्जा u = x प्रत्यास्थता गुणांक x विकृति²
=x 1.2 x 10¹¹ x (2 x 10^-4)²
=x 1.2 x 10¹¹ x 4 x 10^-8
=2.4 x 10³ जूल/मी³

प्रश्न 15.
L लम्बाई तथा A अनुप्रस्थ-काट के क्षेत्रफल का एक तार l लम्बाई से खींचा जाता है। यदि तार के पदार्थ का यंग प्रत्यास्थता गुणांक Y है तो तार का बल नियतांक क्या है?
उत्तर-
तार को । लम्बाई में खींचने के लिए आवश्यक बल

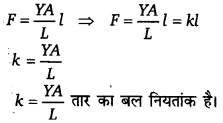
प्रश्न 16.
सम्पीड्यता से क्या तात्पर्य है?
उत्तर-
किसी पदार्थ के आयतन प्रत्यास्थता गुणांक के व्युत्क्रम अर्थात् 1/B को उस पदार्थ की सम्पीड्यता कहते हैं। इसे K से प्रदर्शित करते हैं।

प्रश्न 17.
ठोस, द्रव तथा गैस में से किसकी सम्पीड्यता सबसे अधिक होगी?
उत्तर-
गैस की।

प्रश्न 18.
एक छड़ में अनुदैर्घ्य एवं अनुप्रस्थ विकृति क्रमशः 5 x 10^-3 एवं 2 x 10^-3 हैं। छड़ का प्वासों अनुपात (σ) ज्ञात कीजिए।
हल-
दिया है, छड़ की अनुदैर्ध्य विकृति = 5 x 10^-3
तथा छड़ की अनुप्रस्थ विकृति = 2 x 10^-3

प्रश्न 19.
30 x 10^-3 मी³ आयतन के तरल पर 6 x 10⁶ न्यूटन/मी का दाब बढ़ाने पर उसमें 5 x 10^-7 मी³ आयतन की कमी हो जाती है। तरल का आयतन प्रत्यास्थता गुणांक ज्ञात कीजिए।
हल-

प्रश्न 20.
स्प्रिंग इस्पात की बनाई जाती है, ताँबे की क्यों नहीं?
उत्तर-
समान विरूपक बल लगाने पर इस्पात की स्प्रिंग ताँबे की स्प्रिंग की तुलना में कम खिंचती है। क्योंकि इस्पात का यंग-प्रत्यास्थता गुणांक अधिक होता है। इसके अतिरिक्त, विरूपक बल हटा लेने पर इस्पात की स्प्रिंग ताँबे की स्प्रिंग की तुलना में शीघ्र अपनी पूर्व अवस्था प्राप्त कर लेती है।

प्रश्न 21.
रेल की पटरी I-आकार की क्यों बनाई जाती है?
उत्तर-
रेल की पटरी के ऊपर तथा नीचे के तल अधिक विकृत (strained) होते हैं। अत: उनके क्षेत्रफल अधिक होने चाहिए, जिससे कि उन पर दाब अथवा अभिलम्ब प्रतिबल (F/A) कम लगे। बीच के भाग पर बहुत कम विकृति होती है। अत: वे कम चौड़ाई के बनाये जाते हैं क्योंकि इससे लोहे की बचत होती है।

लघु उत्तरीय प्रश्न

प्रश्न 1.
तन्य पदार्थ एवं भंगुर पदार्थ से क्या तात्पर्य है?
उत्तर-
तन्य पदार्थ (Ductile materials)—ये वे पदार्थ होते हैं जिनमें प्रत्यास्थता की सीमा के आगे प्लास्टिक क्षेत्र बड़ा होता है। ऐसे पदार्थों के । प्रतिबल-विकृति वक्र में भंजक बिन्दु प्रत्यास्थता की सीमा के बिन्दु से काफी दूर ! होता है। इनके तार खींचे जा सकते हैं। इस प्रकार के पदार्थों का प्रयोग स्प्रिंग तथा चादर (sheet) बनाने में किया जाता है।
उदाहरणार्थ-ताँबा, चाँदी, लोहा, ऐलुमिनियम आदि।

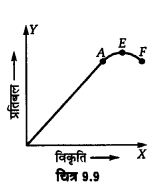
भंगुर पदार्थ (Brittle materials)–ये वे पदार्थ हैं जिनके लिए प्रत्यास्थता । की सीमा से परे प्लास्टिक क्षेत्र बहुत छोटा है। ऐसे पदार्थों के प्रतिबल-विकृति वक्र में भंजक बिन्दु प्रत्यास्थता की सीमा बिन्दु के निकट होता है। (चित्र 9.9)। उदाहरणार्थ-काँच भंगुर पदार्थ है। इनके लिए प्रतिबल-विकृति वक्र संलग्न चित्र की भाँति होता है।

प्रश्न 2.
पॉयसन अनुपात क्या है? आयतन विकृति, पाश्विक विकृति तथा पॉयसन अनुपात में । सम्बन्ध लिखिए।
उत्तर-
पॉयसन अनुपात-पाश्विक विकृति तथा अनुदैर्घ्य विकृति के अनुपात को वस्तु के पदार्थ का पॉयसन अनुपात कहते हैं। इसे σ से प्रदर्शित करते हैं। इसका कोई मात्रक नहीं होता इसीलिए यह एक विमाहीन राशि है।
आयतन विकृति, पाश्विक विकृति तथा पॉयसन अनुपात में सम्बन्ध

(जहाँ A = छड़ की अनुप्रस्थ-काट का क्षेत्रफल)

प्रश्न 3.
हुक का प्रत्यास्थता सम्बन्धी नियम लिखिए।
उत्तर-
सन् 1679 में ब्रिटेन के वैज्ञानिक रॉबर्ट हुक ने प्रयोगों के आधार पर किसी प्रत्यास्थ वस्तु पर लगाये गये विरूपक बल एवं उसके कारण उत्पन्न परिवर्तन में सम्बन्ध स्थापित किया। इसे हुक का नियम कहते हैं जिसका कथन (statement) निम्न प्रकार है
“लघु विकृतियों की सीमा के भीतर, पदार्थ पर कार्यरत् प्रतिबल उसमें उत्पन्न विकृति के अनुक्रमानुपाती होता है।”
अत: प्रतिबल ∝ विकृति
अथवा प्रतिबल = E x विकृति

प्रश्न 4.
यंग-प्रत्यास्थता गुणांक की परिभाषा लिखिए तथा इसका मात्रक व विमा भी लिखिए।
उत्तर-
यंग प्रत्यास्थता गुणांक (Young’s modulus of elasticity)प्रत्यास्थता की सीमा के भीतर अनुदैर्ध्य प्रतिबल और अनुदैर्घ्य विकृति के अनुपात को वस्तु के पदार्थ का यंग प्रत्यास्थता गुणांक कहते हैं। इसे Y से प्रदर्शित करते हैं। यदि L लम्बाई तथा A अनुप्रस्थ-काट के क्षेत्रफल वाले तार पर लम्बाई की दिशा में F बल लगाने से उसकी लम्बाई में वृद्धि । हो, तो

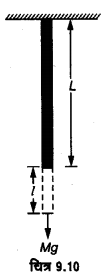
अनुदैर्ध्य प्रतिबल = F/A
तथा अनुदैर्ध्य विकृति = l/L
यंग-प्रत्यास्थता गुणांक
यदि r त्रिज्या अर्थात् A = πr² के किसी तार को एक सिरे पर दृढ़
आधार से बाँधकर, दूसरे सिरे से भार Mg लटकाने पर उसकी लम्बाई में वृद्धि l हो, तो
प्रतिबल = Mg/πr² तथा
विकृति = I/L
(जहाँ r तार की त्रिज्या है।)
इसका मात्रक न्यूटन/मीटर² तथा विमीय सूत्र [ML^-1T^-2] है।

प्रश्न 5.
रबड़ और स्टील में कौन अधिक प्रत्यास्थ है? गणितीय आधार पर समझाइए।
उत्तर-
रबड़ की अपेक्षा स्टील अधिक प्रत्यास्थ है–प्रत्यास्थता पदार्थ का वह गुण है जिसके कारण वस्तु आरोपित विरूपक बल द्वारा उत्पन्न आकार अथवा रूप के परिवर्तन का विरोध करती है। अत: हम कह सकते हैं। कि किसी प्रत्यास्थ वस्तु के आकार अथवा रूप में एक नियत परिवर्तन उत्पन्न करने के लिए जितना अधिक बाह्य बल लगाना होगा, वह वस्तु उतनी ही अधिक प्रत्यास्थ होगी। अत: रबड़ तथा स्टील में कौन अधिक प्रत्यास्थ है, इस बात को उपर्युक्त आधार पर निम्न प्रकार से ज्ञात कर सकते हैं
माना स्टील व रबड़ के दो तार समान लम्बाई L व समान त्रिज्या r के हैं। माना इन पर Mg भार लटकाने से स्टील के तार की लम्बाई में वृद्धि l_s; तथा रबड़ की डोरी की लम्बाई में वृद्धि l_R, है। यदि स्टील व रबड़ के यंग प्रत्यास्थता गुणांक क्रमश: Y_S व Y_R, हैं; तो

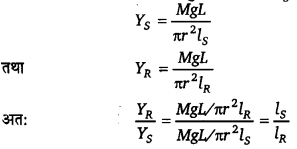
चूँकि रबड़ का तार स्टील के तार की अपेक्षा समान भार के लिए लम्बाई में अधिक खिंचता है, अर्थात् l_R >l_S, इसलिए Y_S > Y_R अर्थात् रबड़ की अपेक्षा स्टील अधिक प्रत्यास्थ है क्योंकि इसके लिए प्रत्यास्थता गुणांक Y_S, का मान अधिक है।

प्रश्न 6.
आयतन प्रत्यास्थता-गुणांक किसे कहते हैं?
उत्तर-
आयतनात्मैक प्रत्यास्थता गुणांक (Bulk modulus of elasticity)-प्रत्यास्थता की सीमा के भीतर, अभिलम्ब प्रतिबल तथा आयतन विकृति के अनुपात को वस्तु के पदार्थ का आयतनात्मक प्रत्यास्थता गुणांक कहते हैं। इसे B से प्रदर्शित करते हैं।
माना किसी वस्तु पर F अभिलम्ब बल लगाकर उसके आयतन में ΔV का परिवर्तन किया जाता है। माना वस्तु का प्रारम्भिक आयतन V तथा अनुप्रस्थ-काट का क्षेत्रफल A है, तो वस्तु पर लगने वला प्रतिबल F/A होगा जोकि वस्तु पर लगाया गया दाब है। अतः

प्रश्न 7.
किसी पदार्थ का यंग प्रत्यास्थता गुणांक 25 x 10¹² न्यूटन/मी² है। इस पदार्थ के 1 मीटर लम्बे तार की लम्बाई में 0.1% वृद्धि करने के लिये कितना बल लगाना होगा? तार कापरिच्छेद क्षेत्रफल 1 मिमी² है।
हल-
दिया है, Y = 25 x 10¹² न्यूटन/मी², L = 1 मी,
l = 0.001.मी = 1 x 10^-3 मी,
A = 1 मिमी² = 10^-6 मी² ।

प्रश्न 8.
धातु की 2 मिमी² एकसमान अनुप्रस्थ-परिच्छेद की एक छड़ को 0°C से 20°C तक गर्म किया जाता है। छड़ का रेखीय प्रसार गुणांक 12 x 10^-6 प्रति °c है। इसका यंग प्रत्यास्थता गुणांक 10¹¹ न्यूटन/मीटर² है। छड़ के प्रति एकांक आयतन में संचित ऊर्जा की गणना कीजिए।
हल-

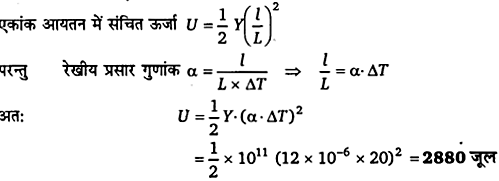
प्रश्न 9.
धातु के एक तार की त्रिज्या 0.35 मिमी है। उसे तार की लम्बाई में 0.2% की वृद्धि करने के लिए कितने बल की आवश्यकता होगी? (Y = 9.0 x 10¹⁰ न्यूटन/मी²)
हल-
यंग प्रत्यास्थता गुणांक के सूत्र

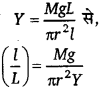
प्रश्न 10.
1.0 मिमी² के एकसमान अनुप्रस्थ-परिच्छेद के तार को 50°C तक गर्म करके दृढतापूर्वक सिरों पर बाँधकर ताना गया है। यदि तार का ताप घटकर 30°C हो जाये तो तार के तनाव में परिवर्तन ज्ञात कीजिए। स्टील कारेखीय प्रसार गुणांक 1.1 x 10^{-5 /}°C तथा यंग प्रत्यास्थता गुणांक 2.0 x 10¹¹ न्यूटन/मी² है।
हल-
तार के ताप में Δt की कमी होने पर, तार में उत्पन्न तनाव बल F = YA α Δt
जहाँ Y तार के पदार्थ का यंग-प्रत्यास्थता गुणांक है, A तार का अनुप्रस्थ-परिच्छेद क्षेत्रफल है तथा α तार के पदार्थ का अनुदैर्ध्य प्रसार गुणांक है।
प्रश्नानुसार, Y = 2.0 x 10¹¹ न्यूटन/मी²,
A = 1.0 मिमी² = 1.0 x 10^-6 मी²,
α = 1.1 x 10^-5 प्रति °C,
At = (50-30)°C = 20°C
F = (2.0 x 10¹¹) x (1.0 x 10^-6) x (1.1 x 10^-5) x 20
= 44 न्यूटन

प्रश्न 11.
एक तार की लम्बाई 1 मी तथा त्रिज्या 2 मिमी है। इससे 2 किग्रा का भार लटकाने पर इसकी लम्बाई में 1 मिमी की वृद्धि हो जाती है। उसी पदार्थ के दूसरे तार, जिसकी लम्बाई 2 मी तथा त्रिज्या 1 मिमी है, पर वही भार लटकाया जाए, तो उसकी लम्बाई में वृद्धि निकालिए।
हल-
यदि L लम्बाई व r त्रिज्या के तार पर Mg भार लटकाने से तार की लम्बाई में वृद्धि l हो, तब

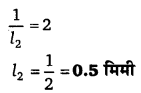
प्रश्न 12.
0.5 मी लम्बाई तथा 1.0 सेमी² परिच्छेद की पीतल की छड़ को लम्बाई की तरफ से 5 किग्रा वजन से दबाया जाता है। छड़ की बढ़ी हुई ऊर्जा की गणना कीजिए। (पीतल का प्रत्यास्थता गुणांक Y = 1.0 x 10¹¹ न्यूटन/मी² ,g = 10 मी/से²)
हल-
ऊर्जा-वृद्धि U = कार्य, W = तथा Y =
अथवा से,
छड़ की बढ़ी हुई ऊर्जा

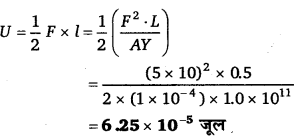
प्रश्न 13.
रबर की एक गेंद को किसी गहरी झील में 100 मी गहराई पर ले जाने से उसके आयतन में 0.2% की कमी हो जाती है। रबर के आयतन प्रत्यास्थता गुणांक की गणना कीजिए। दिया गया है,g = 10.0 मी/से², जल का घनत्व = 1.0 x 10³ किग्रा/मी³।
हल-

विस्तृत उत्तंरीय प्रश्न

प्रश्न 1.
अन्तरा-परमाणु बल नियतांक के लिए सूत्र स्थापित कीजिए।
उत्तर-
अन्तरा-परमाणु बल-नियतांक-हम जानते हैं। कि किसी ठोस में प्रत्येक परमाणु पास वाले परमाणुओं से घिरा । होता है। यह अन्तरा-परमाणविक बलों द्वारा परस्पर बँधे होते हैं तथा स्थिर साम्यावस्था में रहते हैं। जब ठोस पर विरूपक बल लगाया जाता है, तो ठोस के परमाणु अपनी साम्य स्थिति से विस्थापित हो जाते हैं। विरूपक बल को हटा लेने पर अन्तरा-परमाणविक बल उन्हें फिर वापस प्रारम्भिक स्थितियों में ले जाते हैं। ठोस पिण्ड पुनः अपनी प्रारम्भिक स्थिति, आकृति तथा आकार प्राप्त कर लेता है। जब किसी स्प्रिंग को बाह्य बल द्वारा खींचा जाता है, तो स्प्रिंग में उत्पन्न प्रत्यानयन (restoring) बल F, स्प्रिंग की लम्बाई में होने वाली वृद्धि x के अनुक्रमानुपाती होती है।

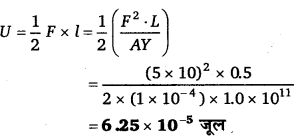
F∝x
⇒ F = kx
जहाँ k एक नियतांक है, जिसे स्प्रिंग का बल नियतांक कहते हैं|

ठीक इसी प्रकार, जब किसी ठोस पर बाह्य बल लगाते हैं, तो परमाणुओं के बीच दूरी बदल जाती है। इससे परमाणुओं के बीच उत्पन्न (अन्तरा-परमाणु) बल F’, उनके बीच दूरी परिवर्तन ∆r के अनुक्रमानुपाती होता है। |
F’ ∝ ∆r ⇒ F = k∆r,
जहाँ k अन्तरा-परमाणु बल नियतांक है।।
माना किसी तार में परमाणुओं के बीच साम्य दूरी r₀ है, तार की लम्बाई l है। तार पर बाह्य बले F लगाने से तार की लम्बाई में वृद्धि ∆l होती है, तो उसके परमाणुओं के बीच की दूरी r₀ से बढ़कर r₀ + ∆r हो जाती है (चित्र 9.11)। तब,
अनुदैर्घ्य विकृति =
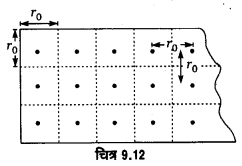
चूंकि परमाणुओं के बीच दूरी r₀ है, अतः तार के अनुप्रस्थ-काट के r₀² क्षेत्रफल में परमाणुओं की औसतन 1 कड़ी (chain) होगी (चित्र 9.12)। अर्थात् अनुप्रस्थ-काट के प्रति एकांक क्षेत्रफल में 1/r₀² कड़ियाँ होंगी। यदि तार का अनुप्रस्थ-काट का क्षेत्रफल A हो, तो उसमें कड़ियों की संख्या A/r₀² होगी। इस प्रकार अन्तरा-परमाणु बल (किसी 1 कड़ी पर लगने वाली बल) |

अतः अन्तरा-परमाणु बल नियतांक k, तार के पदार्थ के यंग-प्रत्यास्थता गुणांक Y तथा तार के परमाणुओं के बीच सामान्य दूरी r₀ , के गुणनफल के बराबर होता है।

प्रश्न 2.
सिद्ध कीजिए कि तार को खींचने पर उसके प्रति एकांक आयतन की प्रत्यास्थ स्थितिज़ ऊर्जा का मान x प्रतिबल x विकृति के बराबर होता है।
उत्तर-
जब किसी तार पर बाह्य बल लगाकर खींचा जाता है तो अन्तरा-परमाणुक बलों के विरुद्ध कुछ कार्य करना पड़ता है, जो तार में प्रत्यास्थ स्थितिज ऊर्जा के रूप में संचित हो जाता है। प्रारम्भ में तार में आन्तरिक बल शून्य है, जो तार की लम्बाई बढ़ने के साथ-साथ बढ़ता जाता है तथा लम्बाई में वृद्धि हो जाने पर बल F हो जाता है जो कि आरोपित बल के बराबर है। इस प्रकार तार की लम्बाई में वृद्धि के लिए औसत आन्तरिक बल = =
अतः तार पर किया गया कार्य W = औसत बल x लम्बाई में वृद्धि = (F/2) x l
यही तार में संचित प्रत्यास्थ स्थितिज ऊर्जा है।
अतः U =
यदि तार की लम्बाई L और अनुप्रस्थ-काट का क्षेत्रफल A हो, तो

= प्रतिबल x विकृति x तार का आयतन
तार के एकांक आयतन में संचित प्रत्यास्थ स्थितिज ऊर्जा
U = प्रतिबल x विकृति (यही सिद्ध करना था।)

प्रश्न 3.
किसी तार के लिए प्रतिबल तथा विकृति के बीच ग्राफ खींचिए। इस ग्राफ से प्रत्यास्थ सीमा, पराभव बिन्दु तथा भंजक बिन्दु समझाइए।
उत्तर-
प्रत्यास्थ सीमा—यह भाग वक्रीय है, अत: विकृति प्रतिबल के अनुक्रमानुपाती नहीं होती है। इस क्षेत्र में हुक का नियम मान्य नहीं होता है। यदि B पर प्रतिबल हटा लिया जाये तो तार अपनी पूर्वावस्था में शीघ्र ही नहीं लौटता है। यदि तार को कुछ समय तक विरूपक बल से मुक्त रखा जाये तो वह अपनी प्रारम्भिक लम्बाई को प्राप्त करेगा। अत: इस बिन्दु B द्वारा निरूपित प्रतिबल को तार की प्रत्यास्थता सीमा (elastic limit) कहते हैं।

पराभव बिन्दु-यह भाग विकृति अक्ष के लगभग समान्तर है। अतः यह उस स्थिति को प्रकट करता है। जब मानो बिना प्रतिबल को बढ़ाये अपने आप ही विकृति बढ़ती रहती है। बिन्दु B, जहाँ पर ऐसी स्थिति , प्रारम्भ होती है, पराभव बिन्दु (yield point) कहलाता है।
भंजक बिन्दु-बिन्दु D से आगे यदि तार पर लटके भार को कम भी किया जाये तो भी तार पतला होता चला जाता है अर्थात् इसका अनुप्रस्थ-परिच्छेद एकसमान नहीं रहता है तथा तार का पदार्थ श्यान तरल (viscous fluid) की भाँति बढ़ना प्रारम्भ हो जाता है एवं एक बिन्दु E तक पहुँचते-पहुँचते तार टूट जाता है। बिन्दु E को भंजक बिन्दु कहते हैं।

प्रश्न 4.
किसी तार को खींचने में किए गए कार्य तथा प्रत्यास्थ स्थितिज ऊर्जा के लिए व्यंजक का निगमन कीजिए।
हल-
किसी तार को खींचने में किया गया कार्य तथा प्रत्यास्थ स्थितिज ऊर्जा के लिए व्यंजक-जब हम किसी तार को खींचते हैं, तो अन्तराणविक बलों के विरुद्ध कुछ कार्य करते हैं जो कि तार में प्रत्यास्थ स्थितिज ऊर्जा के रूप में संचित हो जाता है। अत: तार की प्रत्यास्थता स्थितिज ऊर्जा बढ़ जाती है।
माना एक तार की लम्बाई L तथा परिच्छेद-क्षेत्रफल A है। यदि इस तार की लम्बाई के अनुदिश बले F लगाने से तार की लम्बाई में वृद्धि x हो जाती है। तब ।
अनुदैर्ध्य प्रतिबल = F/A तथा अनुदैर्घ्य विकृति = x/L

प्रश्न 5.
दो क्लैम्पों (दो दृढ़ आधारों) के बीच तने (कसे) तार का ताप बदलने या ठण्डा करने पर तार में उत्पन्न बल के लिए व्यंजक का निगमन कीजिए।
हल-
माना लम्बाई L तथा अनुप्रस्थ-काट क्षेत्रफल A का एक तार दो दृढ़ आधारों के बीच कसा है। जब तार को ठण्डा किया जाता है, तो तार लम्बाई में सिकुड़ता है जिससे कि यह आधारों पर एक बल- आरोपित करता है। माना तार के पदार्थ का यंग-प्रत्यास्थता गुणांक Y व अनुदैर्ध्य प्रसार गुणांक α है। यदि तार के ताप में Δt°C की कमी होने पर तारे की लम्बाई में कमी ΔL हो, तब

We hope the UP Board Solutions for Class 11 Physics Chapter 9 Mechanical Properties Of Solids help you. If you have any query regarding UP Board Solutions for Class 11 Physics Chapter 9 Mechanical Properties Of Solids, drop a comment below and we will get back to you at the earliest.