UP Board Solutions for Class 7 Maths Chapter 12 क्षेत्रमिति ( मेंसुरेशन)
These Solutions are part of UP Board Solutions for Class 7 Maths. Here we have given UP Board Solutions for Class 7 Maths Chapter 12 क्षेत्रमिति ( मेंसुरेशन).
अभ्यास 12 (a)
प्रश्न 1.
निम्नांकित आकृतियों के परिमाप ज्ञात कीजिए:

हल :
(i) आयत का परिमाप = 2 (ले० + चौ०)
= 2 (6 + 3) = 2 × 9 = 18 सेमी
(ii) वर्ग का परिमाप = 4 × भुजा
= 4 × 10 = 40 मिमी
(iii) आयत का परिमाप = 2 (ल० + चौ०)
= 2 (10 + 1.5) = 2 × 11.5 = 23.0 मी
(iv) आकृति का परिमाप = 5 + 1.2 + 1.5 + 1.0 + 2.0 + 1.0 + 1.5 + 1.2
= 14.4 मी
प्रश्न 2.
प्रश्न संख्या 1 में दी गई आकृतियों के क्षेत्रफल ज्ञात कीजिए।
हल :
- आयत का क्षेत्रफल = ल० × चौ० = 6 × 3 = 18 सेमी2
- वर्ग का क्षेत्रफल = भुजा × भुजा = 10 × 10 = 100 मिमी2
- आयत का क्षेत्रफल = ल० × चौ० = 10 × 1.5 = 15 मी2
- दी हुई आकृति का क्षेत्रफल = 5 × 1.2 + 1.0 × 2 = 6 + 2 = 8 मी2
प्रश्न 3.
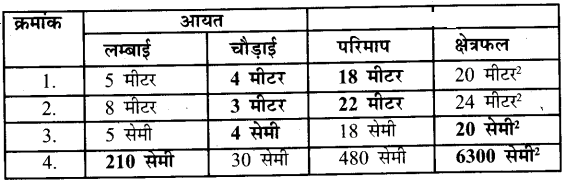
निम्नलिखित सारणी को पूरा कीजिए: (पूरा करके)
उत्तर :
प्रश्न 4.
निशा के विद्यालय में खेल के मैदान की लम्बाई 60 मीटर, चौड़ाई 50 मीटर है। खेल के मैदान का क्षेत्रफल एअर में बताइए।
हल :
आयत का क्षेत्रफल = (60 × 50) मीटर
= 3000 मी2
100 मी2 = 1 एअर
3000 मी2 = 30 एअर
अतः खेल के मैदान का क्षेत्रफल = 30 एअर
प्रश्न 5.
अविनाश के कृषि फार्म की लम्बाई 240 मीटर और चौड़ाई 110 मीटर है। कृषि फार्म का क्षेत्रफल हेक्टेयर में ज्ञात कीजिए।
हल :
फार्म का क्षेत्रफल = ल० × चौ०
= 240 × 110 = 26400 मी2
10000 मी2 = 1 हेक्टेयर
26400 मी2 = 2.64 हेक्टेयर
अतः कृषि फार्म का क्षेत्रफल = 2.64 हेक्टेयर
प्रश्न 6.
एक आयताकार मैदान का क्षेत्रफल 0.5 हेक्टेयर है। यदि इस आयताकार मैदान की एक भुजा 125 मीटर है, तो दूसरी भुजा ज्ञात कीजिए।
हल :
मैदान का क्षेत्रफल = 0.5 हेक्टेयर = 5000 मी2
मैदान की एक भुजा = 125 मीटर
मैदान की दूसरी भुजा = ![]() = 40 मी
= 40 मी
अतः मैदान की दूसरी भुजा की लम्बाई = 40 मी
प्रश्न 7.
एक वर्गाकार टाइल की एक भुजा 12 सेमी है। टाइल को क्षेत्रफल और परिमाप ज्ञात कीजिए।
हल :
वर्गाकार टाइल की एक भुजा = 12 सेमी
टाइल का क्षेत्रफल = 12 × 12 = 144 सेमी2
टाइल का परिमाप = 4 × 12 = 48 सेमी
प्रश्न 8.
एक आयताकार खेत की लम्बाई और चौड़ाई में 3:2 का अनुपात है। खेत के चारों ओर मेड़ बनवाने का खर्च र 1.50 प्रति मीटर की दर से बताइए जबकि खेत का क्षेत्रफल 1.5 हेक्टेयर है।
हल :
माना खेत की लम्बाई = 3 × मी
तथा खेत की चौड़ाई = 2 × मी
परन्तु खेत का क्षेत्रफल = 3x × 2x
. = 1.5 हेक्टेयर = 15000 मी2
2x2 × 3x = 15000
6x2 = 15000
x = ![]() = 2500
= 2500
x = ![]() = 50 मी
= 50 मी
खेत की लम्बाई = 3x = 3 × 50 = 150 मी
तथा खेत की चौड़ाई = 2x = 2 × 50 = 100 मी
खेत का परिमाप = 2 (150 + 100) मी = 2 × 250 = 500 मी
∵ 1 मी मेड़ बनवाने का खर्च = ₹ 1.50
∵ 500 मी मेड़ बनवाने का खर्च = ₹ 500 × 1.50 = 750
प्रश्न 9.
एक कार्यालय के 15 दरवाजों पर खस की टट्टियाँ लगानी है। प्रत्येक दरवाजों की लम्बाई 2.5 मीटर और चौड़ाई 1.2 मीटर है। यदि खस की टट्टी लगाने का खर्च खस के मूल्य सहित ₹ 105.0 प्रति वर्ग मीटर हो, तो कुल कितना खर्च पड़ेगी।
हल :
दरवाजे की लम्बाई = 2.5 मी
दरवाजे की चौड़ाई = 1.2 मी
दरवाजे का क्षेत्रफल = 2.5 × 1.2 = 3 मी2
15 दरवाजों का क्षेत्रफल = 15 × 3 = 45 मी2
∵ 1 मी2 खस लगवाने का खर्च = ₹ 105.0
∵ 45 मी2 खस लगवाने का खर्च = 45 × 105.0 = 4725
अभ्यास 12 (b)
प्रश्न 1.
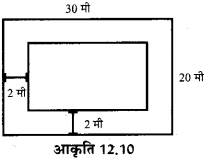
आकृति 12.10 में अन्दर वाले आयत की लम्बाई और चौड़ाई ज्ञात कीजिए
हल :
अन्दर वाले आयत की लम्बाई = (30 – 2 – 2) मी
= (30 – 4) मी = 26 मी
अन्दर वाले आयत की चौड़ाई = (20 – 2 – 2) मी
= (20 – 4) मी = 16 मी
प्रश्न 2.
आकृति 12.11 में बाहर वाले आयत की लम्बाई और चौड़ाई ज्ञात कीजिए

हल :
बाहरी आयत की लम्बाई = (25 + 3 + 3) मी
= (25 + 6) मी = 31 मी।
बाहरी आयत की चौड़ाई = (15 + 3 + 3) मी
= (15 + 6) मी = 21 मी
प्रश्न 3.
आकृति 12.12 में बने छायांकित रास्ते की चौड़ाई 3 मीटर है। बड़े आयत, और रास्ते का क्षेत्रफल ज्ञात करके रिक्त स्थानों की पूर्ति कीजिए (पूर्ति करके)

उत्तर :
- बड़े आयत का क्षेत्रफल 200 मीटर
- छोटे आयत का क्षेत्रफल 56 मीटर [(20 – 3 – 3) × (1043 – 3)] = 56
- छायांकित रास्ते का क्षेत्रफल 144 मीटर (200 – 56) = 144
प्रश्न 4.
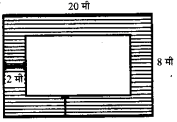
एक हॉल की लम्बाई 20 मीटर और चौड़ाई 8 मीटर है। इसकी दीवारों के चारों ओर फर्श में 2 मीटर चौड़ाई का संगमरमर लगा हुआ है। अपनी अभ्यास पुस्तिका पर एक रफ चित्र बनाकर संगमरमर लगे फर्श का क्षेत्रफल ज्ञात कीजिए।
हल :
हॉल की लम्बाई = 20 मी
हॉल की चौड़ाई = 8 मी
संगमरमर रहित हॉल की लम्बाई = 20 – 2 – 2 = 16 मी
संगमरमर रहित हॉल की चौड़ाई = 8 – 2 – 2 = 4 मी
हॉल का क्षेत्रफल = 20 × 8 = 160 मी2
संगमरमर रहित हॉल का क्षेत्रफल = 16 × 4 = 64 मी
अतः संगमरमर लगे फर्श का क्षेत्रफल = (160 – 64) मी = 96 मी2
प्रश्न 5.
एक वर्गाकार बगीचे के चारों ओर 50 सेमी चौड़ाई का मार्ग बना हुआ है। बगीचे की लम्बाई मार्ग सहित 51 मीटर है। बगीचे का क्षेफफल ज्ञात कीजिए।
हल :
वर्गाकार बगीचे की मार्ग सहित लम्बाई = 51 मी
मार्ग की चौड़ाई = 50 सेमी = 50 मी
वर्गाकार बगीचे की लम्बाई = (51 – 50 – 50) मी
= 50 मी
वर्गाकार बगीचे का क्षेत्रफल = 50 × 50 = 2500 मी2
अभ्यास 12 (c)
प्रश्न 1.
आकृति 12.14 में चित्रों में छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।

हल :
(i) छायांकित भाग का क्षेत्रफल = लंबाई वाले रास्ते का क्षेत्रफल + चौड़ाई वाले रास्ते की क्षेत्रफल — बीच वाले उभयनिष्ठ वर्गाकार रास्ते का क्षेत्रफल
= (50 मीटर × 5 मीटर) + (40 मीटर × 5 मीटर) – (5 मीटर × 5 मीटर)
= 250 मीटर + 200 मीटर2 – 25 मीटर = 425 मीटर2
हल :
(ii) छायांकित भाग का क्षेत्रफल = लम्बाई वाले रास्ते का क्षेत्रफल + चौड़ाई वाले रास्ते का । क्षेत्रफल – बीच वाले उभयनिष्ठ वर्गाकार रास्ते का क्षेत्रफल
= (70 मीटर × 2 मीटर) + (35 मीटर × 2 मीटर) – (2 मीटर × 2 मीटर)
= 140 मीटर2 + 70 मीटर – 4 मीटर = 206 मीटर
प्रश्न 2.
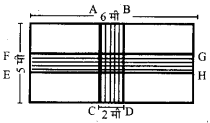
एक आयताकार प्रांगण (Lawu) की लम्बाई 6 मीटर और चौड़ाई 5 मीटर है। इसके मध्य में 2 मीटर चौड़े दो मार्ग इस प्रकार स्थित हैं कि प्रत्येक एक दूसरे को समकोण पर काटते हैं। एक मार्ग की लम्बाई के समान्तर और दूसरा मार्ग चौड़ाई के समान्तर है। मार्ग पर ₹ 25 प्रति वर्ग मीटर की दर से कंकड़ कुटवाने का व्यय ज्ञात कीजिए।
हल :
मार्ग ABCD का क्षेत्रफल = 5 × 2 = 10 वर्ग मी
मार्ग EFGH को क्षेत्रफल = 6 × 2 = 12 वर्ग मी
उभयनिष्ठ वर्ग IJKL का क्षेत्रफल = 2 × 2 = 4 वर्ग मी।
मार्ग का क्षेत्रफल = (12 + 10 – 4): 18 वर्ग मी
अतः ₹ 25 प्रति वर्ग मीटर की दर से कंकड़
कुटवाने का व्यय = 18 × 25 = ₹ 450
प्रश्न 3.
आकृति 12.15 चित्रों में छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।

हल :
पूरे आयत का क्षेत्रफल = 20 × 15 = 300 वर्ग मी
छाया रहित भाग का क्षेत्रफल = 15 × (15 – 3 – 3)
= 15 × 9 = 135 वर्ग मी
छायांकित भाग का क्षेत्रफल = (300 – 135) वर्ग मी
= 165 वर्ग मी।
प्रश्न 4.
आकृति 12.16 में उस भाग का क्षेत्रफल ज्ञात कीजिए जो छायांकित नहीं है।

हल :
छाया रहित भाग की लम्बाई = 75 मी – 10 मी= 65 मी
छाया रहित भाग की चौड़ाई = 24 मी – 10 मी = 14 मी
अतः छाया रहित भाग का क्षेत्रफल = लम्बाई × चौड़ाई
= 65 × 14 = 910 मी
प्रश्न 5.
आकृति 12.17 में एक राजकीय भवन का मानचित्र दिया गया है। इसमें सड़क को बिन्दुदार भाग से दिखाया गया है। इस सड़क की चौड़ाई 2 मीटर है।
(i) सड़क का क्षेत्रफल बताइए।
(ii) सड़क पर ईंट बिछवाने का खर्च ₹ 45 प्रति वर्ग मीटर की दर से क्या होगा?

हल :
(i)
पार्क की लम्बाई = (30 – 2 – 2) = 26 मी
पार्क की चौड़ाई = (20 – 15 – 2) = 3 मी
पार्क का क्षेत्रफल = लम्बाई × चौड़ाई
= 26 × 3 = 78 मी2
संड़क सहित पार्क का क्षेत्रफल = 30 × (20 – 15) = 30 × 5
= 150 मी2
अतः सड़क का क्षेत्रफल = 150 – 78
= 72 मी2
हल :
(ii) ₹ 45 प्रति वर्ग मीटर की दर से
सड़क पर ईंट बिछवाने का खर्च = 72 × 45 = ₹ 3240
प्रश्न 6.
अमरूद के एक बाग की लम्बाई 180 मीटर और चौड़ाई 120 मीटर है। बाग के बीचों-बीच एक दूसरे को समकोण पर काटते हुए 3 मीटर चौड़े दो रास्ते हैं। रास्तों पर मिट्टी डलवाने का खर्च ₹ 12 प्रति मीटर की दर से ज्ञात कीजिए।

हल :
बाग के रास्ते का कुल क्षेत्रफल = 180 × 3 + 120 × 3 – 3 × 3
= 540 + 360 – 9 = 891 मीटर2
अतः रास्तों पर ₹ 12 प्रति मीटर की
दर से मिट्टी डलवाने का खर्च = 891 x 12 = ₹ 10692.00
प्रश्न 7.
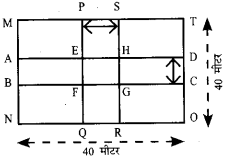
किसी स्कूल के छात्रों ने फाई अभियान के लिए एक रैली निकाली। रैली कुछ समय बाद स्कूल से कुछ दूरी पर बने एक आयताकार पार्क में पहुँचीं जिसकी लम्बाई 40 मीटर, तथा चौड़ाई 25 मीटर है। छात्र तीन समूहों में बँट गये और चित्र के अनुसार पार्क में 5 मीटर चौड़े दो परस्पर लम्बवत् रास्तों के क्रमशः ABEF तथा GCDH भागों को प्रतिम समूह ने PEHS तथा FQRG भागों को द्वितीय समूह ने और EFGH भाग को तृतीय समूह ने साफ किया। प्रत्येक समूह द्वारा साफ किये गये क्षेक्रल ज्ञात कीजिए।
हल :
प्रथम समूह द्वारा साफ किया गया क्षे० = आकृति ABEF तथा GCDH का क्षेत्रफल
= आकृति ABCD का क्षेत्रफल – आकृति EFGH को क्षेत्रफल
= 40 × 5 – 5 × 5
= 200 – 25
= 175 वर्ग मीटर
दूसरे समूह द्वारा साफ किया गया क्षेत्रफल = आकृति PEHS तथा FORG को क्षेत्रफल
= आकृति PQRS का क्षेत्रफल – आकृति EFGH को क्षेत्रफल
= 25 × 5 – 5 × 5
= 125 – 25
= 100 वर्ग मीटर
तीसरे समूह द्वारा साफ किया गया क्षेत्रफल = आकृति EFGH का क्षे
= 5 × 5
= 25 वर्ग मीटर
अभ्यास 12 (d)
प्रश्न 1.
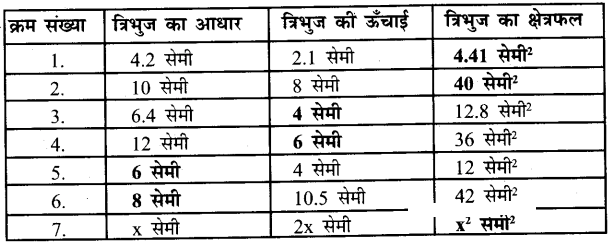
निम्नांकित सारणी में रिक्त स्थानों की पूर्ति कीजिए (पूर्ति करके)
उत्तर :
प्रश्न 2.
एक त्रिभुज का क्षेत्रफल 48 सेमी है। यदि उसकी ऊँचाई 8 सेमी हो, तो त्रिभुज का आधार बताइए।
हल :
त्रिभुज का क्षेत्रफल = 48 सेमी2 त्रिभुज की ऊँचाई = 8 सेमी
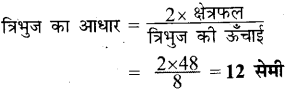
प्रश्न 3.
एक त्रिभुज का आधार 5 सेमी है। यदि त्रिभुज की ऊँचाई, आधार से दुगुनी है, तो त्रिभुज से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
हल :
त्रिभुज का आधार = 5 सेमी
त्रिभुज की ऊँचाई = 5 × 2 = 10 सेमी
त्रिभुज से घिरे क्षेत्र का क्षेत्रफल = ![]() × आधार ४ ऊँचाई
× आधार ४ ऊँचाई
= ![]() × 5 × 10 = 25 सेमी2
× 5 × 10 = 25 सेमी2
प्रश्न 4.
निम्नांकित त्रिभुजों के क्षेत्रफल वर्गमीटर में ज्ञात कीजिए, जबकि उनके आधार और संगत ऊँचाई ज्ञात हैं
(i) आधार = 15 सेमी, ऊँचाई = 8 सेमी
(ii) आधार = 7.5 सेमी, ऊँचाई = 4 सेमी
(iii) आधार = 1.5 मी, ऊँचाई = 0.8 मी।
(iv) आधार = 32 सेमी, ऊँचाई = 105 सेमी
हल :
(i) त्रिभुज का आधार = 15 सेमी = ![]() = 15 मी
= 15 मी
त्रिभुज की ऊँचाई = 8 सेमी = = 08 मी
त्रिभुज का क्षेत्रफल = ![]() × आधार × संगत ऊँचाई
× आधार × संगत ऊँचाई
= ![]() × 0.15 × 08 = .0006 मी
× 0.15 × 08 = .0006 मी
(ii) त्रिभुज का आधार = 7.5 सेमी = 0.075 मी
त्रिभुज की ऊँचाई = 4 सेमी = 0.04 मी
त्रिभुज का क्षेत्रफल = ![]() × 0.075 × 0.04 = 0.0015 मी
× 0.075 × 0.04 = 0.0015 मी
(iii) त्रिभुज का आधार = 1.5 मी
त्रिभुज की ऊँचाई = 0.8 मी।
त्रिभुज का क्षेत्रफल = ![]() × 1.5 × 0.8 = 0.6 मी
× 1.5 × 0.8 = 0.6 मी
(iv) त्रिभुज का आधार = 32 सेमी = 0.32 मी
त्रिभुज का आधार = 105 सेमी = 1.05 मी
अतः त्रिभुज का क्षेत्रफल = ![]() × 0.32 × 1.05 = 0.168 मी
× 0.32 × 1.05 = 0.168 मी
प्रश्न 5.
निम्नांकित त्रिभुजों के क्षेत्रफल ज्ञात कीजिए।
हल :
(i) त्रिभुज का आधार = 6 सेमी 5 सेमी
त्रिभुज की संगत ऊँचाई = 8 सेमी
त्रिभुज का क्षेत्रफल = ![]() × आधार × संगत ऊँचाई
× आधार × संगत ऊँचाई
= ![]() × 6 × 8 = 24 सेमी2
× 6 × 8 = 24 सेमी2
(ii) त्रिभुज का आधार = 12.5 +12.5 = 25 सेमी
त्रिभुज की संगत ऊँचाई = 8 सेमी
त्रिभुजों का क्षेत्रफल = ![]() × 25 × 8= 100 सेमी2
× 25 × 8= 100 सेमी2
त्रिभुज का आधार = 15 सेमी
त्रिभुज की संगत ऊँचाई = 10 सेमी
त्रिभुज का क्षेत्रफल = ![]() × 15 × 10 = 75 सेमी2
× 15 × 10 = 75 सेमी2

प्रश्न 6.
एक सड़क के किनारे एक त्रिभुजाकार यातायात संकेत बोर्ड लगा है जिस पर आगे स्कूल है। लिखा है। यदि संकेत बोर्ड की भुजाएँ क्रमशः 60 सेमी, 80 सेमी एवं 100 सेमी है, तो उसका क्षेत्रफल ज्ञात कीजिए।
हुल :
त्रिभुजाकार बोर्ड की भुजाएँ क्रमशः 60 सेमी, 80 सेमी तथा 100 सेमी है।
त्रिभुजाकार बोर्ड का क्षेत्रफल = ![]()
जहाँ a, b, c त्रिभुजाकार बोर्ड की भुजाएँ है।।
s = ![]()
= ![]() =
= ![]()
= 120 सेमी
अतः त्रिभुजाकार बोर्ड का क्षेत्रफल = ![]()
= ![]()
= ![]()
= ![]()
= 60 × 40
= 2400 वर्ग सेमी
अभ्यास 12 (e)
प्रश्न 1.
निम्नांकित सारणी में दिये गये मापों से प्रत्येक समान्तर चतुर्भुज का क्षेत्रफल ज्ञात कीजिए।

हल :
समान्तर चतुर्भुज को आधार = 8 सेमी
समान्तर चतुर्भुज की ऊँचाई = 3 सेमी
समान्तर चतुर्भुज (1) का क्षेत्रफल = आधार × ऊँचाई = 8, × 3 = 24 सेमी2
समान्तर चतुर्भुज का आधार = 2.8 सेमी
समान्तर चतुर्भुज = 5 सेमी
समान्तर चतुर्भुज (2) का क्षेत्रफल = आधार × ऊँचाई
= 2.8 x 5 = 14.0 सेमी2
समान्तर चतुर्भुज का आधार = 12 मिमी = 1.2 सेमी
समान्तर चतुर्भुज की ऊँचाई = 8.7 सेमी।
समान्तर चतुर्भुज (3) का क्षेत्रफल = आधार × ऊँचाई
= 1.2 × 8.7 = 10.44 सेमी2
समान्तर चतुर्भुज का आधार = 6.5 सेमी
समान्तर चतुर्भुज की ऊँचाई = 4.8 सेमी
समान्तर चतुर्भुज (4) का क्षेत्रफल = आधार × ऊँचाई।
= 6.5 x 4.8 = 31.20 सेमी
समान्तर चतुर्भुज का आधार = 1 मी 5 सेमी = 1.05 मी।
समान्तर चतुर्भुज की ऊँचाई = 45 सेमी = 45 मी
समान्तर चतुर्भुज (5) का क्षेत्रफल = आधार × ऊँचाई
= 1.05 × 45 = 0.4725 मी2
समान्तर चतुर्भुज का आधार = 4.2 डेसीमी = .42 मी
समान्तर चतुर्भुज की ऊँचाई = 25 सेमी = .25 मी
समान्तर चतुर्भुज (6) का क्षेत्रफल = आधार × ऊँचाई
= 42 × 25 = 0.105 मी2
प्रश्न 2.
निम्नांकित समान्तर चतुर्भुजों के क्षेत्रफल ज्ञात कीजिए:

हल :
(i) समान्तर चतुर्भुज का क्षेत्रफल = आधार × ऊँचाई
= 20 × 27 = 540 सेमी2
(ii) समान्तर चतुर्भुज का क्षेत्रफल = आधार × ऊँचाई
= 8 × 16 = 128 सेमी2
(iii) समान्तर चतुर्भुज का क्षेत्रफल = आधार × ऊँचाई
= 8 × 18 = 144 सेमी2
(iv) समान्तर चतुर्भुज का क्षेत्रफल = आधार × ऊँचाई
= 13 × 24 = 312 सेमी2
प्रश्न 3.
उस समान्तर चतुर्भुज की ऊँचाई ज्ञात कीजिए, जिसका क्षेत्रफल 2.25 मी’ और आधार 25 डेसीमी है।
हल :
समान्तर चतुर्भुज का आधार = 25 डेसीमी, आधार = ॐ मी = 2.5 मी

प्रश्न 4.
एक खेत समान्तर चतुर्भुज के आकार का है। इसको आधार 15, डेकामी और ऊँचाई 8 डेकामी है। 5 प्रति वर्गमीटर की दर से सिंचाई कराने का खर्च ज्ञात कीजिए।
हल :
समान्तर चतुर्भुजाकार खेत को क्षेत्रफल = आधार × ऊँचाई
= (15 × 10 मीटर) × (8 × 10 मीटर)
= 12,000 मीटर
1 वर्ग मीटर खेत की सिंचाई कराने का खर्च = ₹ 5
.:. 12,000 वर्ग मीटर खेत की सिंचाई कराने का खर्च = 12,000 × 5
= ₹ 60,000
प्रश्न 5.
आकृति 12.28 में ABCD समान्तर चतुर्भुज है। CFLAB I BGIADI
(i) यदि AB = 16 सेमी, AD = 12 सेमी और CF = 10 सेमी तो BG ज्ञात कीजिए।
(ii) यदि AD = 10 सेमी, CF = 8 सेमी और BG = 12 सेमी तो AB ज्ञात कीजिए।

हल :
(i) समान्तर चतुर्भुज का क्षेत्रफल = आधार × ऊँचाई
AD × BG = AB × CF
12 सेमी ×

(ii) समान्तर चतुर्भुज का क्षेत्रफल = आधार × ऊँचाई
AB × CF = AD × BG
AB × 8 सेमी = 10 सेमी × 12 सेमी

अभ्यास 12 (f)
प्रश्न 1.
नीचे सारिणी में समचतुर्भुज से सम्बन्धित नापें दी हुई हैं। रिक्त स्थानों की पूर्ति कीजिए (पूर्ति करके)
उत्तर :

प्रश्न 2.
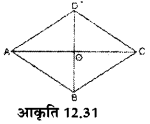
आकृति 12.31 समचतुर्भुज ABCD का क्षेत्रफल 24 वर्ग सेमी और OD=3 सेमी। ज्ञात कीजिए:
(i) विकर्ण BD की लम्बाई
(ii) विकर्ण AC लम्बाई
हलः
(i) समचतुर्भुज के विकर्ण एक-दूसरे को समकोण पर समद्विभाजित करते हैं।
विकर्ण BD = 2 × OD
= 2 × 3 = 6 सेमी
(ii) समचतुर्भुज का क्षेत्रफल = ![]() × पहला विकर्ण × दूसरा विकर्ण
× पहला विकर्ण × दूसरा विकर्ण
24 सेमी = ![]() × AC × BD
× AC × BD
AC = 24 × ![]() = 8
= 8
विकर्ण AC = 8 सेमी
प्रश्न 3.
नीलिमा के समचतुर्भुजाकार प्लॉट का क्षेत्रफल 80 वर्ग मीटर है। यदि इसके एक विकर्ण की लम्बाई 16 मीटर है, तो इसके दूसरे विकर्ण की लम्बाई ज्ञात कीजिए।
हल :
समचतुर्भुज का क्षेत्रफल = ![]() × पहला विकर्ण × दूसरा विकर्ण
× पहला विकर्ण × दूसरा विकर्ण
दूसरा विकर्ण = ![]() = 10
= 10
दूसरा विकर्ण = 10 मीटर
प्रश्न 4.
आकृति 12.32 में दी गई नापों के आधार पर समचतुर्भुज का क्षेत्रफल ज्ञात कीजिए।
हल :
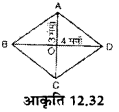
समचतुर्भुज का विकर्ण AC = 2 × OA
= 2 × 3 सेमी = 6 सेमी
विकर्ण BD = 2 × OD
= 2 × 4 सेमी = 8 सेमी
समचतुर्भुज का क्षेत्रफल = ![]() × विकर्ण AC × विकर्ण BD
× विकर्ण AC × विकर्ण BD
= ![]() × 6 सेमी × 8 सेमी
× 6 सेमी × 8 सेमी
= 24 सेमी2
प्रश्न 5.
एक समचतुर्भुजाकार घास के खेत में 20 गायों के चरने के लिए घास है। यदि इस समचतुर्भुज की प्रत्येक भुजा 25 मीटर और एक विकर्ण 30 मीटर है, तो प्रत्येक गाय को चरने के लिए इस घास के खेत का कितना क्षेत्रफल प्राप्त होगा?
हल :

समचतुर्भुज का प्रत्येक भुजा = 25 मीटर
विकर्ण BD की लम्बाई = 30 मीटर
OB = ![]() = 15 मीटर
= 15 मीटर
A OAB में, AB = OA + OB2
(25) = OA + (15)2
625 = OA2 + 225
OA = 625 – 225 = 400
OA = 400 = 20 मीटर
समचतुर्भुज ABCD का क्षेत्रफल = ![]() × विकर्णो का गुणनफल
× विकर्णो का गुणनफल
= ![]() × 40 × 30
× 40 × 30
= 600 वर्ग मीटर
20 गायों के चरने के लिए घास = समचतुर्भुज का क्षेत्रफल
= 600 वर्ग मीटर
1 गाय के चरने के लिए घास = ![]() = 30 वर्ग मीटर
= 30 वर्ग मीटर
अभ्यास 12 (g)
प्रश्न 1.
निम्नांकित सारणी में घनाभ की लम्बाई, चौड़ाई और ऊँचाई दी गई है। प्रत्येक घनाभ का सम्पूर्ण पृष्ठ ज्ञात कीजिए।

(i) घनाप का सम्पूर्ण पृष्ठ = 2 (b + bh + hl)
= 2 (5 × 4 + 4 × 3 + 3 × 5) सेमी2
= 2 (20 + 12 + 15) सेमी।2
= 2 × 47 सेमी = 94 सेमी2
(ii) घनाभ का सम्पूर्ण पृष्ठ = 2 (/b + bh + hi)
= 2 (6 × 3 + 3 × 2 + 2 × 6) सेमी2
= 2 (18 + 6 + 12) सेमी2
= 2 × 36 सेमी = 72 सेमी2
(iii) घनाभ का सम्पूर्ण पृष्ठ = 2 (lb + bh + hi)
= 2 (10 × 8 + 8 × 5 + 5 × 10) सेमी2
= 2 (80 + 40 + 50) सेमी2
= 2 × 170 सेमी = 340 सेमी2
(iv) घनाभ का सम्पूर्ण पृष्ठ = 2 (lb + bh + hl)
= 2 (4 × 1.7 + 1.7 × 2.3 + 2.3 × 4)
= 2 (6.8 + 3.91 + 9.2) सेमी2
= 2 × 19.91 सेमी = 39.82 सेमी2
(v) घनाभ का सम्पूर्ण पृष्ठ = 2 (Ib + bh + hi)
= 2(![]() × 4 × 4 ×
× 4 × 4 × ![]() +
+ ![]() ×
× ![]() )
)
= 2 (22 + 42 + ![]() ) सेमी2
) सेमी2
= 2 (64 + ![]() ) सेमी2
) सेमी2
= ![]() सेमी2
सेमी2
= (128 + 115.5) सेमी2
= 243.5 सेमी2
(vi) घना’ का सम्पूर्ण पृष्ठ = 2 (lb + bh + hl)
= 2 (16 × 8 + 8 × 6 + 6 × 16)
= 2 (128 + 48 + 96) सेमी2
= 2 × 272 सेमी = 544 सेमी2
प्रश्न 2.
नीचे दी गई भुजा की नाप वाले घन का सम्पूर्ण पृष्ठ ज्ञात कीजिए।
(i) भुजा = 18 सेमी
(ii) भुजा = 8.8 सेमी
(iii) भुजा = 1.2 सेमी।
(iv) भुजा = 110 सेमी
हल :
(i) घन का सम्पूर्ण पृष्ठ = 6 × (भुजा)2
= 6 × (18) सेमी2
= 6 × 324 सेमी2 = 1944 सेमी2
(ii) घन का सम्पूर्ण पृष्ठ = 6 × (भुजा)2
= 6 × (8.8) सेमी2
= 6 × 77.44 सेमी2 = 464.64 सेमी2
(iii) घर का सम्पूर्ण पृष्ठ = 6 × (भुजा)2
= 6 × 1.2 सेमी2
= 6 × 1.44 सेमी2 = 8.64 सेमी2
(iv) घर का सम्पूर्ण पृष्ठ = 6 × (भुजा)2
= 6 × (110) सेमी2
= 6 × 12100 सेमी2 = 72600 सेमी2
प्रश्न 3.
दिए गए घनाभ के कुल पृष्ठ का क्षेत्रफल ज्ञात कीजिए।
हल :
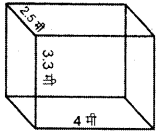
घनाभ के कुल पृष्ठों का क्षेत्रफल
= 2 (/b + bh + hl)
= 2 (4 × 3.3 + 3.3 × 2.5 + 2.5 × 4) मी2
= 2 (13.2 + 8.25 + 10.0) मी2
= 2 (31.45) मी2
= 62.90 मी2
प्रश्न 4.
अभिषेक के कमरे की लम्बाई 4 मीटर, चौड़ाई 3.5 मीटर और ऊँचाई 3 मीटर है। इस कमरे की चारों दीवारों का क्षेत्रफल ज्ञात कीजिए।
हल :
कमरे की चारो दीवारों का क्षेत्रफल = 2 (लम्बाई + चौड़ाई) × ऊँचाई
= 2 (4 + 3.5) × 3 मी2
= 2 × 7.5 × 3 मी2
= 45 मी2
प्रश्न 5.
एक घनाकार बक्से की एक भुजा की लम्बाई 1 मीटर 30 सेमी है। बक्से का सम्पूर्ण पृष्ठ ज्ञात कीजिए।
हल :
घनाकार बक्से की भुजा (a) = 1 मीटर 30 सेमी
= (100 + 30) सेमी2 = 130 सेमी
.:. घनाकार बक्से का सम्पूर्ण पृष्ठ = 6 × (भुजा)2
= 6 × (130) सेमी2
= 6 × 16,900 सेमी2
= 1,01,400 सेमी2
प्रश्न 6.
रहीम के कमरे की लम्बाई 3.5 मीटर, चौड़ाई 3 मीटर, ऊँचाई 3 मीटर है। इसकी चारों दीवारों पर 15 प्रति वर्ग मीटर की दर से सफेदी कराने का व्यय ज्ञात कीजिए।
हल :
कमरे की चारों दीवारों का क्षेत्रफल = 2 (लम्बाई + चौड़ाई) x ऊँचाई
= 2 (3.5 + 3) × 3 मी2
= 2 × 6.5 × 3 मी2
= 39 मी
अतः चारों दीवारों पर 15 प्रति वर्ग
मीटर की दर से सफेदी कराने का व्यय = ₹ 15 × 39
= ₹ 585
प्रश्न 7.
एक घनाकार डिब्बे की एक भुजा 10 सेमी है तथा एक अन्य घनाभ के आकार के डिब्बे की लम्बाई, चौड़ाई तथा ऊँचाई क्रमशः 12.5 सेमी, 10 सेमी तथा 8 सेमी है। किस डिब्बे का पार्श्व पृष्ठीय क्षेत्रफ अधिक है और कितना अधिक है?
हल :
घनाकार डिब्बे की भुजा = 10 सेमी
घनाकार डिब्बे का सम्पूर्ण पृष्ठ = 6 x (भुजा)2
= 6 × (10)2
= 6 × 100 = 600 वर्ग सेमी
घनाभ के आकार के डिब्बे की लम्बाई = 12.5 सेमी
चौड़ाई = 10 सेमी
ऊँचाई = 8 सेमी
घनाभ के आकार के डिब्बे का सम्पूर्ण पृष्ठ = 2(lb + bh + b)
=2 × (12.5 × 10 + 10 × 8+ 12.5 × 8)
= 2 × (125 + 80 + 100)
= 2 × 305 = 610 वर्ग सेमी
घनाभ के आकार के डिब्बे का सम्पूर्ण पृष्ठ अधिक है।
अन्तर = 610 – 600
= 10 वर्ग सेमी
प्रश्न 8.
प्रदीप स्वीट स्टॉल को मिठाइयाँ पैक करने के लिए गत्ते के घनाभ के आकार के 200 डिब्बे बनवाने हैं, जिनकी लम्बाई 25 सेमी, चौड़ाई 20 सेमी तथा ऊँचाई 5 सेमी है। यदि गत्ते का मूल्य ₹ 40 प्रति वर्ग मीटर है, तो डिब्बे बनवाने की कुल कीमत ज्ञात कीजिए।
हल :
घनाकार के डिब्बे की लम्बाई = 25 सेमी
चौड़ाई = 20 सेमी।
ऊँचाई = 5 सेमी
घनीभ के आकार के डिब्बे का सम्पूर्ण पृष्ठ = 2(lb + bh + b)
= 2 × (25 × 20 + 20 × 5 + 25 × 5)
= 2 × (500+ 100 + 125)
= 2 × 725 = 1450 वर्ग सेमी
200 डिब्बे का सम्पूर्ण पृष्ठ = 200 × 1450
= 290000 वर्ग सेमी
= 29 वर्ग मीटर
1 वर्ग मीटर गत्ते का मूल्य = ₹ 40
= 40 x 29
= ₹ 1160
दक्षता अभ्यास – 12
प्रश्न 1.
निम्नांकित आकृति 12.38 में छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।
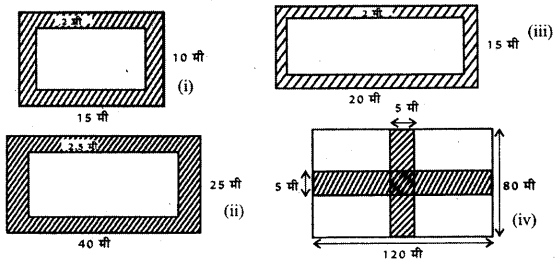
हल :
(i) बाहरी आयत का क्षेत्रफल = लम्बाई × चौड़ाई
= 15 मीटर × 10 मीटर = 150 मीटर2
भीतरी आयत का क्षेत्रफल = लम्बाई × चौड़ाई
= (15 – 4) मीटर × (10 – 4) मीटर2
= 11 × 6 मीटर2 = 66 मीटर2
अतः छायांकित भाग का क्षेत्रफल = 150 मीटर – 66 मीटर2 = 84 मीटर2
(ii) बाहरी आयते को क्षेत्रफल = 20 मीटर × 15 मीटर = 300 मीटर
भीतरी आयते की क्षेत्रफल = (20 – 4) मीटर × (15 – 4) मीटर2
= 16 × 11 मीटर = 176 मीटर2
अंतः छायांकित भाग का क्षेत्रफल = 300 मीटर – 176 मीटर = 124 मीटर2
(iii) बाहरी आयत का क्षेत्रफल = 40 मीटर × 25 मीटर = 1,000 मीटर2
भीतरी आयते का क्षेत्रफल = (40-5) मीटर × (25-5) मीटर2
= 35 × 20 मीटर = 700 मीटर2
छायांकित भाग का क्षेत्रफल = 1000 मीटर’ – 700 मीटर2
= 300 मीटर।2
(iv) छायांकित भाग का क्षेत्रफल = लम्बाई वाले रास्ते का क्षेत्रफल +
चौड़ाई वाले रास्ते को क्षेत्रफलं – बीच वाले उभयनिष्ठ भाग को क्षेत्रफल
= (120 × 5) + (80 × 5) – (5 × 5)
= 600 + 400 – 25 = 975 मीटर2
प्रश्न 2.
एक वर्गाकार पार्क की सीमा से लगा हुआ पार्क के अन्दर चारों ओर 1 मीटर चौड़ाई का मार्ग है। पार्क की लंबाई 30 मीटर है। पार्क के शेष भाग में र6 प्रति वर्ग मीटर की दर से घास लगवाने का व्यय ज्ञात कीजिए।
हल :
वर्गाकार पार्क की बाहरी भुजा = 30 मीटर
वर्गाकार पार्क के अन्दर चारों ओर 1 मीटर चौड़ाई का मार्ग है।
वर्गाकार पार्क की भीतरी भुजा = (30 -2) मीटर = 28 मीटर
वर्गाकार पार्क का भीतरी क्षेत्रफल = (28 मीटर)2 = 784 मीटर2
अतः ₹ 6 प्रति वर्ग मीटर की दर से घास लगवाने का व्यय = 784 × ₹ 6
= ₹ 4704
प्रश्न 3.
उस त्रिभुज को क्षेत्रफल ज्ञात कीजिए जिस का आधार 9.6 सेमी और ऊँचाई 5 सेमी है।
हल :
त्रिभुज का क्षेत्रफल = 1/2 × आधार × ऊँचाई
= 1 × 9.6 × 5 = 24 सेमी2
प्रश्न 4.
उस त्रिभुज की ऊँचाई ज्ञात कीजिए जिसका क्षेत्रफल 45 सेमी है तथा आधार 15 सेमी है।
हल :
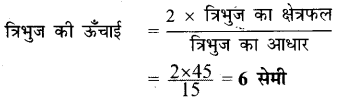
प्रश्न 5.
आकृति 12.39 चतुर्भुज ABCD का क्षेत्रफल ज्ञात कीजिए, ₹ 2० जिसमें AC=48 सेमी, BF = 10 सेमी और DE=20 सेमी।
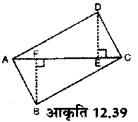
हल :
चतुर्भुज ABCD का क्षेत्रफल ![]() × AC × (BF +DE)
× AC × (BF +DE)
= ![]() × 48 × (10 + 20) = 24 × 30 सेमी2
× 48 × (10 + 20) = 24 × 30 सेमी2
= 720 सेमी2
प्रश्न 6.
उस समान्तर चतुर्भुज का क्षेत्रफल ज्ञात कीजिए, जिसको आधार 7 सेमी और ऊँचाई 4.3 सेमी हो।
हल :
समान्तर चतुर्भुज का क्षेत्रफल = आधार × ऊँचाई
= 7 × 4.3 = 30.1 सेमी
प्रश्न 7.
12 सेमी भुजा के दो घन सटाकर रखे गए हैं। सटाकर रखने से बने घनाभ का सम्पूर्ण पृष्ठ ज्ञात कीजिए।
हल :
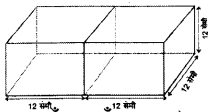
घनाभ की लम्बाई = 12 + 12 = 24 सेमी।
घनाभ की चौड़ाई = 12 सेमी
घनाभ की ऊँचाई = 12 सेमी
घनाभ का सम्पूर्ण पृष्ठ क्षेत्रफल = 2 (ल० × चौ० + चौ० × ऊँ० + ऊँ० × ल०)
= 2 (24 × 12 + 12 × 12 + 12 × 24) सेमी2
= 2 (288 + 144 + 288)
= 2 × 720 = 1440 सेमी2
We hope the UP Board Solutions for Class 7 Maths Chapter 12 क्षेत्रमिति ( मेंसुरेशन)