These Solutions are part of UP Board Solutions for Class 7 Maths. Here we have given UP Board Solutions for Class 7 Maths Chapter 10 चतुर्भुज.

अभ्यास 10 (a)

प्रश्न 1.
आकृति चतुर्भुज ABCD में,

(a) कितनी भुजाएँ हैं?
उत्तर :
चार
(b) कितने अन्त: कोण हैं?
उत्तर :
चार
(c) सम्मुख कोणों के कितने युग्म हैं?
उत्तर :
दो
(d) संलग्न भुजाओं के कितने जोड़े हैं?
उत्तर :
चार जोड़े
(e) कितने विकर्ण होंगे?
उत्तर :
दो
(f) क्या AB, BC, CD और DA में से कोई विकर्ण है?
उत्तर :
नहीं
(g) कितने शीर्ष हैं?
उत्तर :
चार

प्रश्न 2.
उपर्युक्त आकृति के आधार पर अपनी अभ्यास-पुस्तिका में रिक्त स्थानों की पूर्ति कीजिए (पूर्ति करके)
उत्तर :

(a) Q अन्तः क्षेत्र में स्थित है।
(b) R बाह्य क्षेत्र में स्थित है।
(c) T भुजा DC पर स्थित है।

प्रश्न 3.
किसी चतुर्भुज ABCD से सम्बन्धित निम्नांकित कथनों में रिक्त स्थानों की पूर्ति कीजिए (पूर्ति करेक )
उत्तर :

(a) दो सम्मुख शीर्षों को मिलाने से विकर्ण बनता है।
(b) शीर्ष A और शीर्ष C को मिलाने से विकर्ण बनता है।
(c) शीर्ष D और शीर्ष B को मिलाने से विकर्ण बनता है।
(d) चतुर्भुज का एक विकर्ण इसे दो त्रिभुजों में विभाजित करता है।

प्रश्न 4.
अपनी अभ्यास-पुस्तिका में रिक्त स्थानों की पूर्ति कीजिए ( पूर्ति करके)
उत्तर :

(a) सम चतुर्भुज की चारों भुजाएँ बराबर होती हैं।
(b) आयत के चारों कोण समकोण होते हैं।
(c) वर्ग की चारों भुजाएँ बराबर और चारों कोण समकोण होते हैं।
(d) समलम्ब चतुर्भुज की सम्मुख भुजाओं का एक युग्म समान्तर होता है।

अभ्यास 10 (b)

प्रश्न 1.
किसी चतुर्भुज का एक कोण 60° तथा शेष तीन अन्तः कोण बराबर हैं। शेष प्रत्येक कोण की माप ज्ञात कीजिए।
अत : माना शेष प्रत्येक अन्तः कोण की माप = x°
प्रश्नानुसार, 60° + x° +x° +x° = 360°
⇒ 60° + 3x° = 360°
⇒ 3x° = 360° – 60° 3x° = 300°
⇒ x० = = 100°
⇒ शेष प्रत्येक कोण का मान = 100°, 100°, 100°

प्रश्न 2.
किसी चतुर्भुज के दो कोण 60° और 120° के हैं। शेष दो कोण समान हैं। शेष प्रत्येक कोण का मान ज्ञात कीजिए।
हल :
माना चतुर्भुज के शेष प्रत्येक कोण की माप = x°
प्रश्नानुसार, 60° + 120° + x° +x° = 360°
⇒ 180° + 2x = 360°
⇒ 2x° = 360° – 180° 2x° = 180°
⇒ x° = = 90°
अतः शेष प्रत्येक कोण का मान = 90°, 90°

प्रश्न 3. किसी चतुर्भुज के अन्तः कोण बराबर हैं। प्रत्येक कोण को मान ज्ञात कीजिए।
हल :
माना चतुर्भुज का प्रत्येक कोण = x°
प्रश्नानुसार, x° + x° + x° + x° = 360°
⇒ 4x° = 360°
⇒ x° = = 90°
अतः चतुर्भुज के प्रत्येक कोण का मान = 90°, 90°, 90°, 90°

प्रश्न 4.
यदि किसी चतुर्भुज के दो अन्तः कोण सम्पूरक हैं, तो शेष दो कोणों का योग ज्ञात कीजिए।
हल :
चतुर्भुज के दो अन्तः कोणों का योग = 180°
माना चतुर्भुज के शेष दो अन्तः कोणों का योग = x°
प्रश्नानुसार, x° + 180° = 360°
⇒ x° = 360° – 180°
⇒ x° = 180°
अत: शेष दो कोणों का योग = 180°

प्रश्न 5.
एक 45° के ∠BAC की रचना कीजिए। इसके अंतः क्षेत्र में बिन्दु P से रेखी खंड BA और AC पर लम्ब PN और PM खींचिए। ∠NPM का मान । ज्ञात कीजिए।
हल :

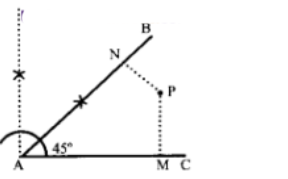
∠ BAC + ∠ PNA + ∠ NPM + ∠ PMA= 360°
⇒ 45° + 90° +∠ NPM + 90° = 360°
⇒ ∠ NPM = 360° – 225°
⇒ ∠ NPM = 135°

प्रश्न 6.
यदि चतुर्भुज के अन्तः कोणों का अनुपात 3:4:5:6 हो, तो प्रत्येक कोण का मान ज्ञात कीजिए।
हल :
माना चतुर्भुज के अन्तः कोण = 3x°, 4x°, 5x°, 6x
प्रश्नानुसार, 3x° +4x° + 5x° + 6x° = 360°
⇒ 18x° = 360°
⇒ x° = = 20°
अतः चतुर्भुज के अन्तः कोण 3x° = 3×20° = 60°
⇒ 4x° = 4 x 20° = 80°
⇒ 5x = 5 x 20 = 100°
⇒ 6x° = 6x 20° = 120°

प्रश्न 7.
यदि चतुर्भुज के तीन बाह्य कोण क्रमशः 80°, 100° और 120° हों, तो चौथे अन्तः कोण का मान ज्ञात कीजिए।
हल :
चतुर्भुज के तीन अन्तः कोण = 80°, 100° व 120°
माना चतुर्भुज का चौथा अन्तः कोण = x°
प्रश्नानुसार, 80° + 100° + 120° + x° = 360°
⇒ 300° + x° = 360°
⇒ x° = 360° -300°
⇒ x° = 60°
अतः चौथे अन्तः कोण का मान = 60° है।

प्रश्न 8.
यदि चतुर्भुज के अन्तः कोण A, B, C और D इस प्रकार हों कि इनके अनुपात ∠ A : ∠ B = 1 : 2, ∠B: C = 2 : 3, 4C : ∠D = 3:4, तो प्रत्येक कोण का मान ज्ञात कीजिए।
हल :
∠ A: ∠ B = 1 : 2, 2 B : ∠C = 2: 3, ∠C: ∠ D = 3:4
∠ A: ∠ B : ∠C: ∠ D = 1:2: 3:4
आनुपातिक योग = 1 + 2 + 3 +4 = 10
∵ चतुर्भुज के चारों अन्तः कोणों का योग 360° होता है।
∴ ∠ A = = 36०
∴ ∠ B = = 72०
∴ ∠ C = = 108०
∴ ∠D = = 144°

प्रश्न 9.
एक समद्विबाहु त्रिभुज ABC का शीर्ष कोण 40° है। त्रिभुज की भुजा AB और AC के मध्य बिन्दु क्रमशः M और N हैं। बिन्दुओं M और N को मिलाइए। इस प्रकार बने चतुर्भुज BMNC के अन्तः कोण BMN तथा कोण CNM का योग ज्ञात कीजिए। इनका अलग-अलग मान भी ज्ञात कीजिए।
हल :
समद्विबाहु त्रिभुज ABC में,
∠ B = ∠ C
∠ A + ∠ B + ∠ C = 180°
40° +∠ C + ∠ C = 180°
2∠ C 180° – 40° = 140°
∠ C = = 70°
∠ AMN= ∠ B = 70°
∠ ANM= ∠ C = 70°
∠ BMN = 180° – 70° = 110°
∠ CNM = 180° – 70° = 110°
∠ BMN +∠ CNM = 110° + 110° = 220°

अभ्यास 10 (c)

प्रश्न 1.
समान्तर चतुर्भुज का एक अन्तः कोण 30° है। शेष कोणों के मान ज्ञात कीजिए।
हल :
समान्तर चतुर्भुज के सम्मुख कोण बराबर होते हैं।
माना शेष दोनों सम्मुख कोण = x°
समान्तर चतुर्भुज का एक अन्त: कोण = 30°
इसका सम्मुख कोण = 30°
हम जानते हैं कि x° +x° + 30° + 30° = 360°
⇒ 2x° + 60° = 360°
⇒ 2x° = 360° – 60°= 300°
⇒ x° = = 150°
अतः शेष कोण = 30°, 150°, 150°

प्रश्न 2.
समान्तर चतुर्भुज की किसी भुजा पर बने कोणों में 40° का अन्तर है। प्रत्येक कोण का माने ज्ञात कीजिए।
हल :
माना समान्तर चतुर्भुज की भुजा पर बना एक कोण = x°
अतः समान्तर चतुर्भुज की भुजा पर बना दूसरा कोण = 40° + x°
⇒ x° + x° + (40° + x°) + (40° + x°) = 360°
⇒ 4x° + 80° = 360°
⇒ 4x° = 360° – 80° = 280°
⇒ x° = = 70°
अतः समान्तर चतुर्भुज की भुजा पर बना दूसरा कोण = 40° + 70° = 110°
अतः प्रत्येक कोण = 70°, 110°, 70°, 110°

प्रश्न 3.
समान्तर चतुर्भुज की किसी भुजा पर बने कोणों में 1 और 3 का अनुपात हो। तो प्रत्येक कोण का मान ज्ञात कीजिए।
हल :
माना समान्तर चतुर्भुज का पहला कोण = x°
प्रश्नानुसार, समान्तर चतुर्भुज का दूसरा कोण = 3x°
समान्तर चतुर्भुज में सम्मुख कोण बराबर होते हैं। ∴ x° + 3x° +x° + 3x°= 360°
⇒ 8x° = 360°
⇒ x° = = 45°
समान्तर चतुर्भुज का दूसरा कोण = 3 x 45° = 135°
अतः प्रत्येक कोण का मान = 45, 135०, 45, 135०

प्रश्न 4.
समान्तर चतुर्भुज की संलग्न भुजाएँ 4 सेमी और 6 सेमी हैं। चतुर्भुज की अन्य दो भुजाओं की माप बताइए।
हल : समान्तर चतुर्भुज की संलग्न भुजाएँ 4 सेमी और 6 सेमी हैं। चूँकि समान्तर चतुर्भुज की सम्मुख भुजाएँ समान होती हैं।  अतः चतुर्भुज की अन्य दो भुजाएँ भी 4 सेमी और 6 सेमी होंगी।

प्रश्न 5.
समान्तर चतुर्भुज की संलग्न भुजाएँ 8 सेमी और 6 सेमी हैं। चतुर्भुज का परिमाप ज्ञात कीजिए।
हल :
समान्तर चतुर्भुज की संलग्न भुजाएँ 8 सेमी और 6 सेमी हैं। चूँकि समान्तर चतुर्भुज की सम्मुख भुजाएँ समान होती हैं।  अत: चतुर्भुज की अन्य दो भुजाएँ भी 8 सेमी और 6 सेमी की होंगी।
अतः चतुर्भुज का परिमाप = 8 + 6 + 8 +6 = 28 सेमी

प्रश्न 6.
समान्तर चतुर्भुज की दो संलग्न भुजाओं का अनुपात 1:2 है। यदि इसका परिमाप 30 सेमी हो, तो प्रत्येक भुजा की माप ज्ञात कीजिए।
हल :
माना समान्तर चतुर्भुज की दो संलग्न भुजाएँ = x, 2x सेमी
प्रश्नानुसार, x + 2x + x + 2x = 30
⇒6 x = 30
⇒ x = = 5
⇒ 2x = 2×5 = 10
अतः समान्तर चतुर्भुज की प्रत्येक भुजा की माप = 5 सेमी, 10 सेमी 5 सेमी, 10 सेमी

प्रश्न 7.
आकृति 10.24 PQRS एक समान्तर चतुर्भुज है। रेखाखण्ड OP,OQ,OR और OS को माप कर सत्यापित कीजिए कि OP = OR तथा OQ = OS
हल :
आकृति 10.24 PQRS एक समान्तर चतुर्भुज है। PR और SQ समान्तर चतुर्भुज के विकर्ण है।

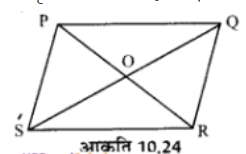
OP = PR
तथा 05 = QS
क्योंकि समान्तर चतुर्भुज के विकर्ण एक दूसरे को समद्विभाजित करते हैं।
अतः OP = OR
तथा OS = OQ

प्रश्न 8.
आकृति 10.25 में समलम्ब PQRS में कोण P और S के मान ज्ञात कीजिए।
हल :

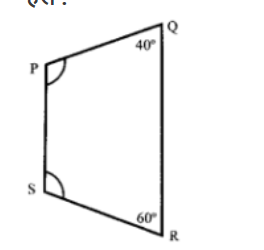
चतुर्भुज PQRS में,
∠ P + ∠Q = 180°
∠ P+ 40° = 180°
∠ P = 180° – 40° = 140°
∠ S +∠R = 180°
∠ S + 60° = 180°
∠ S = 180° – 60° = 120°

अभ्यास 10 (d)

प्रश्न 1.
आकृति 10.30 में ABCD एक समान्तर चतुर्भुज है। वे प्रतिबंध बताइए जब कि यह

(i) समचतुर्भुज होगा,
(ii) आयत होगा,
(iii) वर्ग होगा।

हल :

(i) ABCD समचतुर्भुज होगा, यदि संलग्न भुजाएँ समान हों। आकृति 10.30
(ii) ABCD आयत होगा, यदि प्रत्येक कोण 90° हो।
(iii) ABCD वर्ग होगा, यदि प्रत्येक 90° तथा संलग्न भुजाएँ बराबर हों।

प्रश्न 2.
समान्तर चतुर्भुज ABCD में निम्नांकित प्रत्येक कथन के सत्य होने पर आकृति को किस नाम से पुकारेंगे?

(i) AB = BC
(ii) ∠ ABC = 90°
(iii) ∠ ABC = 90′ और AB = BC

हल :

(i) यदि AB = BC, तो आकृति समचतुर्भुज होगी।
(ii) यदि ∠ ABC = 90°, तो आकृति आयत होगी।
(iii) यदि – ABC = 90° और AB = BC, तो आकृति वर्ग होगी।

प्रश्न 3.
वर्ग में (पूर्ति करके)
उत्तर :

• भुजाओं की लम्बाइयाँ बराबर होती हैं।
• विकर्ण बराबर होते हैं।
• प्रत्येक कोण समकोण होता है।
• विकर्ण एक दूसरे के लम्बवत् होती हैं।

प्रश्न 4.
यदि किसी वर्ग के विकर्ण का वर्ग 50 वर्ग सेमी है, तो इसका परिमाप ज्ञात कीजिए।
हुल :

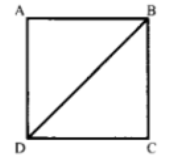
वर्ग के विकर्ण का वर्ग BD² = 50 वर्ग सेमी
⇒ AB² + AD² = BD²
⇒ a² + a² = 50
⇒ 2a² = 50
⇒ a² =
⇒ a² = 25
⇒ a = 5 सेमी
वर्ग का परिमाप = 4 × 5 = 20 सेमी

प्रश्न5.
आप की पुस्तक के एक पन्नेका एक विकर्ण दूसरे विकर्ण से छोटा है। क्या यह पुस्तक आयताकार है?
हल :
यदि पुस्तक के एक पन्ने का एक विकर्ण दूसरे विकर्ण से छोटा है तो यह पुस्तक आयताकार नहीं होगी।

प्रश्न 6.
एक आयत बनाइए जिसकी संलग्न भुजाएँ क्रमशः 6 सेमी और 8 सेमी हैं। इनके विकणे को मापिए और पाइथागोरस प्रमेय से माप का सत्यापन कीजिए।
हल :

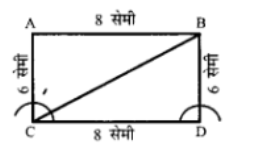
मापने पर, विकर्ण BC = 10 सेमी
पाइथागोरस प्रमेय से,
BC² = AB² + AC² = 6² + 8²
BC = = = = 10 सेमी

प्रश्न 7.
एक आयत बनाइए जिसकी संलग्न भुजाएँ क्रमशः 5 सेमी और 12 सेमी हैं। इनके विकर्णो को मापिए और पाइथागोरस प्रमेय से इसका सत्यापन कीजिए।
हल :

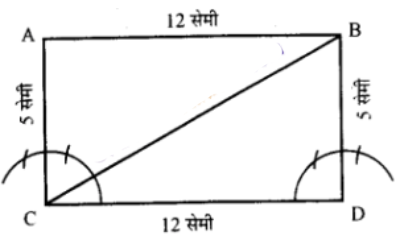
नापने पर,
विकर्ण AC = 13 सेमी
पाइथागोरस प्रमेय से,
AC² = 12² + 5²
AC = =
= 13 सेमी

प्रश्न 8.
समचतुर्भुज का एक विकर्ण यदि इसकी एक भुजा के बराबर हो, तो इनके सभी अन्तः कोणों का मान ज्ञात कीजिए।
हलः

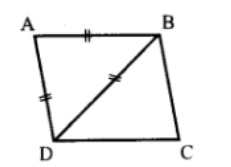
यदि समचतुर्भुज का एक विकर्ण इसकी एक भुजा के बराबर है, तो वह दूसरी भुजा के भी बराबर होगा।
∆ABD में,
AB = BD = DA
⇒ ∠ DAB = ∠ABD = ∠ADB
∵ ∠ DAB +∠ABD +∠ADB = 180°
⇒ ∠ DAB +2 DAB +∠ DAB = 180°
⇒ 3∠ DAB = 180°
⇒ ∠ DAB =
⇒ ∠ DAB = 60°
⇒ ∠ ABD = 60°
⇒ ∠ ADB = 60°
इसी प्रकार ∠ BCD = 60°
∠ABC = 2 ∠ABD = 2 × 60° = 120°
∠ADC = 2 ∠ ADB = 2 × 60° = 120°

We hope the UP Board Solutions for Class 7 Maths Chapter 10 चतुर्भुज help you.