UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 7 Correlation (सहसंबंध)

पाठ्य-पुस्तक के प्रश्नोत्तर

प्रश्न 1.
कद (फुटों में) तथा वजन (किलोग्राम में) के बीच सहसंबंध गुणांक की इकाई है
(क) किग्रा/फुट
(ख) प्रतिशत
(ग) अविद्यमान
उत्तर-
(ग) अविद्यमान

प्रश्न 2.
सरल सहसंबंध गुणांक का परास निम्नलिखित होगा
(क) 0 से अनन्त तक
(ख) -1 से +1 तक
(ग) ऋणात्मक अनन्त (infinity) से धनात्मक अनन्त तक
उत्तर-
(ख) -1 से +1 तक

प्रश्न 3.
यदि r, धनात्मक है तो x और y के बीच का संबंध इस प्रकार का होता है
(क) जब y बढ़ता है तो x बढ़ता है
(ख) जब y घटता है तो x बढ़ता है।
(ग) जब y बढ़ता है तो x नहीं बदलता है।
उत्तर-
(क) जेब y बढ़ता है तो x बढ़ता है।

प्रश्न 4.
यदि r = 0 तब चर x और y के बीच
(क) रेखीय संबंध होगी।
(ख) रेखीय संबंध नहीं होगा
(ग) स्वतंत्र होगा।
उत्तर-
(ग) स्वतंत्र होगा।

प्रश्न 5.
निम्नलिखित तीन मापों में, कौन-सा माप किसी भी प्रकार के संबंध की माप कर सकता
(क) कार्ल पियर्सन सहसंबंध गुणांक
(ख) स्पीयरमैन का कोटि सहसंबंध
(ग) प्रकीर्ण आरेख
उत्तर-
(क) कार्ल पियर्सन सहसंबंध गुणांक

प्रश्न 6.
यदि परिशुद्ध रूप से मापित आँकड़े उपलब्ध हों, तो सरल सहसंबंध गुणांक
(क) कोटि सहसंबंध गुणांक से अधिक सही होता है।
(ख) कोटि सहसंबंध गुणांक से कम सही होता है।
(ग) कोटि सहसंबंध की ही भाँति सही होता है।
उत्तर-
(ग) कोटि सहसंबंध की ही भाँति सही होता है।

प्रश्न 7.
साहचर्य के माप के लिए को सहप्रसरण से अधिक प्राथमिकता क्यों दी जाती है?
उत्तर-
सहसंबंध चरों के बीच संबंधों की गहनता एवं दिशा का अध्ययन एवं मापन करता है। सहसंबंध सह-प्रसरण का मापन करता है न कि कार्यकारण संबंध का। इसीलिए r को सह प्रसरण से अधिक प्राथमिकता दी जाती है।

प्रश्न 8.
क्या आँकड़ों के प्रकार के आधार परे r, -1 तथा + 1 के बाहर स्थित हो सकता है?
उत्तर-
सहसंबंध गुणांक का मान -1 तथा +1 के बीच स्थित होता है -1

प्रश्न 9.
क्या सहसंबंध के द्वारा कार्यकारण संबंध की जानकारी मिलती है?
उत्तर-
नहीं, सहसंबंध के द्वारा कार्यकारण संबंध की जानकारी नहीं मिलती है। सहसंबंध केवल चरों के बीच संबंधों की गहनता एवं दिशा का अध्ययन एवं मापन करता है। सहसंबंध सहप्रसरण का मापन करता है। न कि कार्यकारण संबंध का।

प्रश्न 10.
सरल सहसंबंध गुणांक की तुलना में कोटि सहसंबंध गुणांक कब अधिक परिशुद्ध होता है।
उत्तर-
सरल सहसंबंध गुणांक तथा कोटि सहसंबंध गुणांक दोनों ही दो चरों के मध्य रेखीय संबंध मापते हैं। परन्तु जब चरों को सार्थक रूप से मापन नहीं किया जा सकता; जैसे—कीमत, आय, वजन आदि, तब कोटि सहसंबंध गुणांक साधारण सहसंबंध की तुलना में अधिक परिशुद्ध होता है।

प्रश्न 11.
क्या शून्य सहसंबंध का अर्थ स्वतंत्रता है?
उत्तर-
यदि r = 0, तो दो चर असहसंबंधित होते हैं। यद्यपि इनके बीच कोई रेखीय संबंध नहीं होता। तथापि इनके बीच दूसरे प्रकार के सहसंबंध हो सकते हैं। अत: शून्य सहसंबंध का अर्थ सदैव स्वतंत्रता नहीं

प्रश्न 12.
क्या सरल सहसंबंध गुणांक किसी भी प्रकार के संबंध को माप सकता है?
उत्तर-
हाँ, सरल सहसंबंध गुणांक किसी भी प्रकार के संबंध को माप सकता है।

प्रश्न 13.
एक सप्ताह तक अपने स्थानीय बाजार से 5 प्रकार की सब्जियों की कीमतें प्रतिदिन एकत्र करें। उनका सहसंबंध गुणांक परिकलित कीजिए। इसके परिणाम की व्याख्या कीजिए।
उत्तर-
विद्यार्थी स्वयं करें।

प्रश्न 14.
अपनी कक्षा के सहपाठियों के कद मापिए। उनसे उनके बैंच पर बैठे सहपाठी का कद पूछिए। इन दो चरों का सहसंबंध गुणांक परिकलित कीजिए और परिणाम का निर्वचन कीजिए।
उत्तर-
विद्यार्थी स्वयं करें।

प्रश्न 15.
कुछ ऐसे चरों की सूची बनाएँ जिनका परिशुद्ध मापन कठिन हो?
उत्तर-
ऐसे चर जिनका परिशुद्ध मापन कठिन है

• तापमान एवं आइसक्रीम की बिक्री।
• तापमान एवं समुद्र की तरफ जाने वाले पर्यटक।

प्रश्न 16.
r के विभिन्न मापों +1, -1 तथा 0 की व्याख्या कीजिए।
उत्तर-

• r का धनात्मक मान दर्शाता है कि दोनों चर एक ही दिशा में गतिमान होते हैं।
• r का ऋणात्मक मान दो चरों के मध्य प्रतिलोम संबंध दर्शाता है।
• यदि r = 0, तो दो चर असहसंबंधित होते हैं।
• यदि r = ± 1 या r = -1 हैं तो सहसंबंध पूर्ण है व इनके बीच सुनिश्चित सहसंबंध है।

प्रश्न 17.
पियर्सन सहसंबंध गुणांक से कोटि सहसंबंध गुणांक क्यों भिन्न होता है?
उत्तर-
सामान्यत: कार्ल पियर्सन सहसंबंध गुणांक एवं कोटि सहसंबंध गुणांक की विशेषताएँ एकसमान होती हैं। दोनों ही मामलों में सहसंबंध गुणांक का मान ± 1 के मध्य होता है। परंतु कोटि सहसंबंध के परिणाम पियर्सन सहसंबंध के परिणाम की भाँति शुद्ध नहीं होता। सामान्यत: r ≤ r अर्थात् rk, r की तुलना में बराबर अथवा कम होता है। इसका कारण यह है कि कोटि सहसंबंध में चर मूल्यों के बजाय कोटियों (ranks) का प्रयोग किया जाता है। पियर्सन सहसंबंध गुणांक चरों के चरम मूल्यों से भी प्रभावित होता है। जबकि कोटि सहसंबंध में चरम मूल्यों का कोई प्रभाव नहीं पड़ता।

प्रश्न 18.
पिताओं (x) और उनके पुत्रों (y) के कदों का माप नीचे इंचों में दिया गया है। इन दोनों के बीच सहसंबंध गुणांक को परिकलित कीजिए-

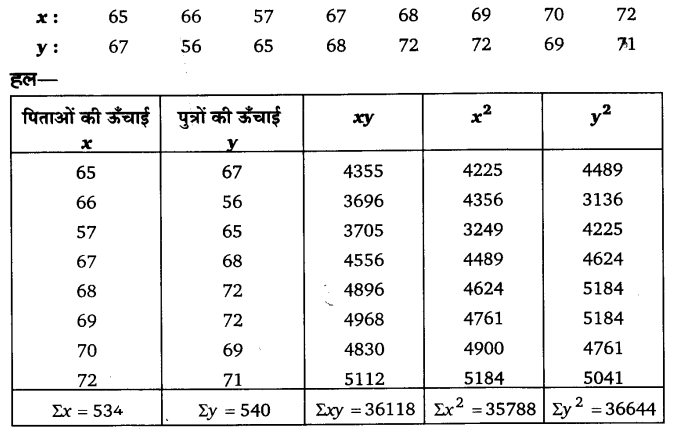
प्रश्न 19.
x और y के बीच सहसंबंध गुणांक को परिकलित कीजिए और उनके संबंध पर टिप्पणी कीजिए-

प्रश्न 20.
x और y के बीच सहसंबंध गुणांक को परिकलित कीजिए और उनके संबंध पर टिप्पणी कीजिए-

परीक्षोपयोगी प्रश्नोत्तर
बहुविकल्पीय प्रश्न

प्रश्न 1.
दो चर मूल्यों के मध्य परिवर्तन का अनुपात समान हो तो उनमें सहसंबंध पाया जाता है
(क) सरल
(ख) रेखीय
(ग) अरेखीय
(घ) धनात्मक
उत्तर-
(ख) रेखीय

प्रश्न 2.
सहसंबंध गुणांक का मान …………. के बीच होता है।
(क) +2 तथा -2
(ख) +1 तथा -1
(ग) +3 तथा -3
(घ) +0 तथा -1
उत्तर-
(ख) +1 तथा -1

प्रश्न 3.
सहसंबंध गुणांक निकालने का सरलतम सूत्र है

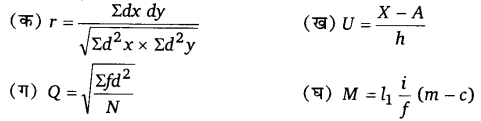
उत्तर-

प्रश्न 4.
“यदि यह सत्य होता कि अधिकांश उदाहरणों में दो चर (two variables) सदैव एक ही दिशा में या विपरीत दिशा में घटने-बढ़ने की प्रवृत्ति रखते हैं तो हमें यह मानते हैं कि उनमें एक संबंध पाया जाता है।” कथन है-
(क) पियर्सन का।
(ख) सेलिगमैन का
(ग) प्रो० किंग का
(घ) डॉ० बाउले को
उत्तर-
(ग) प्रो० किंग का

प्रश्न 5.
सहसंबंध के प्रकार हैं-
(क) दो
(ख) तीन
(ग) चार
(घ) पाँच
उत्तर-
(ख) तीन

अतिलघु उत्तरीय प्रश्न

प्रश्न 1.
सहसम्बन्ध की परिभाषा दीजिए।
उत्तर-
दो श्रेणियों अथवा समूहों के बीच कार्यकारण सम्बन्ध को सहसम्बन्ध कहते हैं।

प्रश्न 2.
‘सहसम्बन्ध तकनीक के प्रतिपादक कौन हैं?
उत्तर-
सर्वप्रथम फ्रांस के खगोलशास्त्री ब्रावे ने इसके मूल तत्त्वों का प्रतिपादन किया था। तत्पश्चात् इस सिद्धान्त को आधुनिक रूप फ्रांसिस गाल्टन तथा कार्ल पियर्सन ने दिया।

प्रश्न 3.
ऋणात्मक व धनात्मक सहसम्बन्ध में अन्तर बताइए।
उत्तर-
धनात्मके सहसम्बन्ध में दो पदमालाओं में परिवर्तन एकसमान दिशाई होता है जबकि ऋणात्मक सहसम्बन्ध में यह परिवर्तन विपरीत दिशाई होता है।

प्रश्न 4.
पूर्ण सहेसम्बन्ध की स्थिति कब होती है?
उत्तर-
जब दो चर मूल्यों में परिवर्तन एक ही दिशा में और एक ही अनुपात में हो तो इनमें पूर्ण सहसम्बन्ध होगा।

प्रश्न 5.
सहसम्बन्ध की उच्च सीमा क्या है?
उत्तर-
± 0.75 से ± 1 के मध्य।

प्रश्न 6.
बिन्दुरेखीय रीति द्वारा सहसम्बन्ध ज्ञात करने का प्रमुख दोष क्या है?
उत्तर-
बिन्दुरेखीय विधि द्वारा सहसम्बन्ध की केवल दिशा को ही ज्ञात किया जा सकता है उसकी मात्रा को नहीं।

प्रश्न 7.
कार्ल पियर्सन के सहसम्बन्ध गुणांक का प्रमुख गुण क्या है?
उत्तर-
इस विधि के द्वारा केवल दिशा व मात्रा का अनुमान ही नहीं बल्कि उसका परिमाणात्मक माप भी प्राप्त होता है।

प्रश्न 8.
कार्ल पियर्सन द्वारा प्रतिपादित सहसम्बन्ध गुणांक एक आदर्श माप क्यों है?
उत्तर-
यह माप समान्तर माध्य और प्रमाप विचलन पर आधारित है। इसलिए यह एक आदर्श माप है।

प्रश्न 9.
कार्ल पियर्सन के सहसम्बन्ध गुणांक की दो मान्यताएँ बताइए।
उत्तर-

• दो घटनाओं के मध्य परस्पर कारण और परिणाम का सम्बन्ध पाया जाता है।
• दोनों समंक श्रेणियों में रेखीय सहसम्बन्ध पाया जाता है।

प्रश्न 10.
स्पियरमैन की कोटि अन्तर विधि का प्रयोग किन परिस्थितियों में उपयुक्त है?
उत्तर-
यह विधि उन परिस्थितियों में उपयुक्त है जहाँ तथ्यों का प्रत्यक्ष संख्यात्मक माप सम्भव न हो तथा उन्हें एक निश्चित क्रम के अनुसार रखा जा सके।

प्रश्न 11.
स्पियरमैन कोटि अन्तर विधि का सूत्र बताइए।
उत्तर-

प्रश्न 12.
यदि दो मूल्य बराबर आकार के हों और उन्हें बराबर क्रम प्रदान किए जाएँ तो संशोधित सूत्र क्या होगा?
उत्तर-

लघु उत्तरीय प्रश्न

प्रश्न 1.
सहसम्बन्ध का महत्त्व बताइए।
उत्तर-
सहसम्बन्ध का महत्त्व
सांख्यिकी में सहसम्बन्ध का सिद्धान्त अत्यधिक उपयोगी है। इस सिद्धान्त का विकास फ्रांसिस गाल्टन व कार्ल पियर्सन ने प्राणिशास्त्र तथा जनन-विद्या की अनेक समस्याओं के आधार पर किया है। सहसम्वन्ध के द्वारा ही अनेक वैज्ञानिक, सामाजिक तथा आर्थिक क्षेत्रों में दो-या-दो से अधिक घटनाओं के आपसी सम्बन्धों को स्पष्टीकरण मिलता है। इसकी सहायता से इस बात का आभास होता है कि विभिन्न समस्याओं के कारण तथा परिणाम में कितना और किस प्रकार का सम्बन्ध है। प्रतीपगमन (Regression), विचरण अनुपात (Ratio of Variation), आन्तरगणन (Interpolation), बाह्यगणन (Extrapolation) आदि अनेक सांख्यिकीय धारणाएँ सहसम्बन्ध सिद्धान्त पर आधारित हैं।

सांख्यिकी के अतिरिक्त; मनोविज्ञान, शिक्षा, कृषि, अर्थशास्त्र आदि के क्षेत्रों में भी सहसम्बन्ध का विशेष महत्त्व है। अर्थशास्त्र में सहसम्बन्ध के उपयोग के बारे में नीसवेंजर लिखते हैं-“सहसम्बन्ध विश्लेषण आर्थिक व्यवहार को समझने में योग देता है, विशेष महत्त्वपूर्ण चरों, जिन पर अन्य चर निर्भर करते हैं, को खोजने में सहायता देता है, अर्थशास्त्री को उन सुझावों को स्पष्ट करता है जिनसे गड़बड़ी फैलती है तथा उसे उन उपायों का सुझाव देता है जिनके द्वारा स्थिरता लाने वाली शक्तियाँ प्रभावित हो सकती हैं।”

प्रश्न 2.
कार्ल पियर्सन के सहसम्बन्ध गुणांक की विशेषताएँ बताइए।
उत्तर-

1. यह रीति गणितीय दृष्टि से उपयुक्त है क्योंकि यह प्रमाप विचलन एवं समान्तर माध्य पर आधारित है।
2. यह रीति बीजगणितीय दृष्टि से उत्तम है क्योंकि यह श्रेणी क सभी मूल्यों व पदों पर आधारित होती
3. इस रीति से सहसम्बन्ध की दिशा, मात्रा व सीमाओं का ज्ञान सुविधापूर्वक हो जाता है।
4. यह सदैव ± 1 के मध्य रहता है।

प्रश्न 3.
कार्ल पियर्सन के सहसम्बन्ध गुणांक के लघु रीति द्वारा गणन क्रिया के विभिन्न सूत्र बताइए। इनमें कौन-सा सूत्र सरल है?
उत्तर-
लघु रीति द्वारा सहसम्बन्ध गुणांक के निम्नलिखित चार सूत्र हैं.-

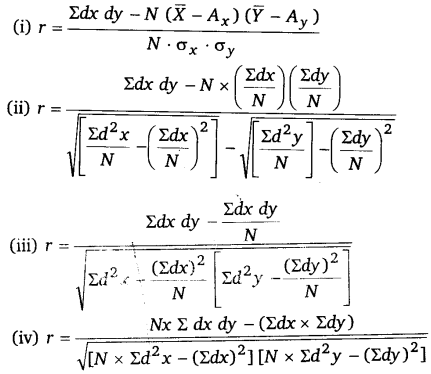
उपर्युक्त में चतुर्थ सूत्र सरलतम है। इसलिए प्रश्नों के हल में इसी का प्रयोग किया गया है।

प्रश्न 4.
सहसम्बन्ध गुणांक के प्रमुख गुण बताइए।
उत्तर-
सहसम्बन्ध गुणांक के प्रमुख गुण निम्नलिखित हैं

1. r की कोई इकाई नहीं होती, यह एक संख्या मात्र है।
2. F का ऋणात्मक मान विपरीत दिशाई सम्बन्ध बतलाता है। उदाहरणार्थ जब कीमत बढ़ती है तो माँग घट जाती है।
3. यदि r धनात्मक है तो यह बताता है कि दोनों चर एक ही दिशा में गतिमान हुए हैं। उदाहरणार्थ सिंचाई सुविधाओं में वृद्धि कृषि-उत्पादन में वृद्धि करती है।
4. सहसम्बन्ध गुणांक को मान +1 तथा -1 के बीच होता है।
5. r का मान उद्गम परिवर्तन या पैमाने के परिवर्तन से प्रभावित नहीं होता है।

प्रश्न 5.
निम्नलिखित आँकड़ों से अल्पकालीन उच्चावचनों का सहसम्बन्ध गुणांक निकालिए।

हल-
नोट- सर्वप्रथम 3 वर्षीय चल माध्य निकाले जाएँगे और उनसे विचलन लिए जाएँगे।

प्रश्न 6.
सहसम्बन्ध गुणांक के परिकलन की पद-विचलन विधि समझाइए। निम्नलिखित उदाहरण में पद विचलन विधि द्वारा सहसम्बन्ध गुणांक का परिकलन कीजिए।
उत्तर-
पद विचलन विधि-इस विधि का प्रयोग तब किया जाता है जब चरों के मान ऊँचे होते हैं। इसके अन्तर्गत x एवं y चरों को निम्नांकित प्रकार से परिवर्तित किया जाता है-

प्रश्न 7.
एक सौन्दर्य प्रतियोगिता में 10 प्रतियोगियों को तीन निर्णायकों के द्वारा निम्न क्रम प्राप्त हुए हैं। यह निर्धारण करने के लिए कोटि सहसम्बन्ध गुणांक का परिकलन कीजिए कि कौन-सा
युगल सन्दरता सम्बन्धी सामान्य रुचियों के अधिक निकट है।

हल-
सहसम्बन्ध परिकलित करने के लिए निम्नांकित संयोग बनाए जाएँगे

• प्रथम एवं द्वितीयक निर्णायक (R₁ वे R₂)
• द्वितीय व तृतीय निर्णायक (R₂ व R₃)
• प्रथम वे तृतीय निर्णायक (R₁ व R₃)

प्रश्न 8.
कोटि अन्तर सहसम्बन्ध गुणांक के गुण व दोष बताइए।
उत्तर-
गुण-

• यह समझने में अपेक्षाकृत सरल है।
• यह विधि गुणात्मक चरों में सहसम्बन्ध को ज्ञात करने में श्रेष्ठ है।
• केवल कोटि दिए होने पर भी सहसम्बन्ध की गणना की जा सकती है।

दोष-

• समूह आवृत्ति आवंटन शृंखलाओं में इस विधि का प्रयोग नहीं किया जा सकता।
• 20 से अधिक मदों वाली श्रृंखला में इस विधि का प्रयोग करना अत्यधिक कठिन है।

दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
सहसंबंध का अर्थ एवं परिभाषा दीजिए। यह कितने प्रकार का होता है?
उत्तर-
सहसंबंध का अर्थ एवं परिभाषा
वास्तविक जीवन में दो या दो से अधिक श्रृंखलाओं में परस्पर संबंध पाया जाता है। उदाहरण के लिए कीमत के बढ़ने पर माँग में कमी होती है। मुद्रा की पूर्ति बढ़ने पर कीमत स्तर में वृद्धि होती है। रोजगार में वृद्धि होने पर उत्पादन में वृद्धि होती है। ऐसी परिस्थितियों में दो या दो से अधिक सांख्यिकी श्रृंखलाओं का एक साथ अध्ययन करना आवश्यक हो जाता है। इस अध्ययन का उद्देश्य विभिन्न सांख्यिकीय शृंखलाओं में पारस्परिक संबंधों की जानकारी प्राप्त करना होता है। सहसंबंध इन पारस्परिक संबंधों की गणना करने की सांख्यिकीय विधि है।

जब दो चर राशियों में से एक चर राशि के बढ़ने से दूसरी चर राशि (variable) में वृद्धि हो या कमी हो एवं एक चर राशि की कमी से दूसरी चर राशि में वृद्धि हो या कमी हो तो उन दोनों चर राशियों में सहसंबंध पाया जाता है। सहसंबंध की प्रमुख परिभाषाएँ निम्नलिखित हैं-

1. प्रो० किंग के अनुसार- “यदि यह सत्य होता है कि अधिकांश उदाहरणों में दो चर (two variables) सदैव एक ही दिशा में या विपरीत दिशा में घटने-बढ़ने की प्रवृत्ति रखते हैं तो हम यह मानते हैं कि उनमें सहसंबंध पाया जाता है।”
2. टटिल के अनुसार- “दो या दो से अधिक चरों के सहविचरणों के विश्लेषण को सहसंबंध कहते है।”
3. प्रो० क्रॉक्सटन व काउडेन के अनुसार- “जब संबंधों की संख्यात्मक प्रकृति होती है तो उसे ज्ञात करने, मापने एवं एक सूत्र में स्पष्ट करने के उचित सांख्यिकीय यंत्र को सहसंबंध कहते हैं।”
4. प्रो० कॉनर के अनुसार- “जब दो या दो से अधिक परिमाण सहानुभूति में परिवर्तित होते हैं। जिससे एक के परिवर्तन के फलस्वरूप दूसरे में भी परिवर्तन हो जाता है तो वे राशियाँ ‘सहसंबंधित’ कहलाती हैं।”
5. प्रो० बोडिंगटन के अनुसार- “जब कभी दो या अधिक समूहों अथवा वर्गों अथवा समंकमालाओं में निश्चित संबंध विद्यमान हो तो उनमें सहसंबंध का होना कहा जाता है।”

सहसंबंध के प्रकार

1.”धनात्मक अथवा ऋणात्मक सहसंबंध- यदि एक चर मूल्य घटने पर दूसरा चर मूल्य भी घटे अथवा एक चर मूल्य के बढ़ने पर दूसरा चर मूल्य भी बढ़े तो ऐसा सहसंबंध धनात्मक होता है। मूल्य एवं पूर्ति में इसी प्रकार का सहसंबंध पाया जाता है। ऋणात्मक सहसंबंध उस दशा में होता है जब एक चर मूल्य के घटने पर दूसरा चर मूल्य बढ़ता हो तथा एक चर मूल्य के बढ़ने पर दूसरे चर मूल्य में कमी होती हो। मूल्य एवं माँग में इसी प्रकार का | सहसंबंध पाया जाता है।
2. सरल, आंशिक अथवा बहुगुणी सहसंबंध- दो चर मूल्यों के सहसंबंध को सरल सहसंबंध कहते हैं। आंशिक सहसंबंध में दो मूल्यों में एक अन्य स्वतंत्र चर मूल्य का समावेश करके सहसंबंध ज्ञात किया जाता है। बहुगुणी सहसंबंध में तीन या अधिक चर मूल्यों के मध्य सहसंबंध का अध्ययन किया जाता है।

3. रेखीय तथा अरेखीय सहसंबंध- यदि दो चर मूल्यों के मध्य परिवर्तन का अनुपात समान होता है तो उनमें रेखीय सहसंबंध होगा। इन चर मूल्यों को यदि बिन्दुरेखीय पत्र पर अंकित किया जाए तो बिन्दु एक सीधी रेखा के रूप में होंगे। अरेखीय सहसंबंध जिसे वक्ररेखीय सहसंबंध’ भी कहते हैं, में एक चर मूल्य के परिवर्तनों की मात्रा व दूसरे चर मूल्य के परिवर्तनों की मात्रा एक अनुपात में नहीं होगी। इन चर मूल्यों को बिन्दु रेखा पर अंकित करने पर वक्र बन जाता है।

प्रश्न 2.
सहसंबंध का क्या अर्थ है? सहसंबंध के परिमाण (degrees) कितने प्रकार के होते हैं?
उत्तर-
नोट- सहसंबंध के अर्थ के लिए विस्तृत उत्तरीय प्रश्न संख्या 1 का उत्तर देखिए।
सहसंबंध का परिमाण
सहसंबंध निम्नलिखित परिमाण में हो सकता है-

1. पूर्ण सहसंबंध-
   • जब दो श्रेणियों में परिवर्तन एक ही दिशा में तथा समान अनुपात में होते हैं। तो उनमें पूर्ण धनात्मक सहसंबंध पाया जाता है। ऐसी दशा में सहसंबंध गुणांक (r) + 1 होता है।
   • जब दो श्रेणियों में परिवर्तन विपरीत दिशा में किंतु समान अनुपात में होते हैं तो उनमें पूर्ण ऋणात्मक सहसंबंध पाया जाता है। ऐसी दशा में सहसंबंध गुणांक (r) – 1 होता है। सामाजिक विज्ञान में पूर्ण सहसंबंध नहीं पाया जाता।
2. सहसंबंध का अभाव- जब दो चरों अर्थात् श्रेणियों में तनिक भी परस्पर आश्रितता नहीं पायी जाती अर्थात् वे एक श्रेणी के मूल्यों को प्रभावित नहीं करते तो दोनों चरों अथवा श्रेणियों में सहसंबंध नहीं होता अर्थात् उनमें सहसंबंध का अभाव पाया जाता है। ऐसी दशा में सहसंबंध गुणांक (r) शून्य (0) होता है।
3. सीमित सहसंबंध- जब दोनों श्रेणियों में परिवर्तन समान रूप में नहीं होते, तो उनमें सहसंबंध सीमित मात्रा में पाया जाता है। इस प्रकार का सहसंबंध धनात्मक व ऋणात्मक दोनों प्रकार का हो संकता है। सामान्यत: यह 1 के मध्य होता है। परिमाण की दृष्टि से सीमित सहसंबंध तीन प्रकार के हो सकते हैं-
   • उच्च स्तरीय सहसंबंध- यदि सहसंबंध गुणांक + 0.75 से लेकर + 1 के बीच होता है तो इसमें उच्च मात्रा का सहसंबंध माना जाता है।
   • मध्यम स्तरीय सहसंबंध- जब सहसंबंध गुणांक + 0.25 से लेकर + 0.75 तक रहता है तो इसमें मध्यम मात्रा का सहसंबंध पाया जाता है।
   • निम्न स्तरीय सहसंबंध- जब सहसंबंध गुणांक शून्य (0) से अधिक परंतु + 0.25 से कम रहता है तो इसमें निम्न स्तरीय सहसंबंध पाया जाता है।

प्रश्न 3.
सहसंबंध का अर्थ एवं महत्त्व बताइए। सहसंबंध को ज्ञात करने की कौन-कौन-सी विधियाँ हैं?
उत्तर-
नोट- सहसंबंध के अर्थ के लिए विस्तृत उत्तरीय प्रश्न संख्या 1 का उत्तर देखिए।
सहसंबंध का महत्त्व
सांख्यिकीय में सहसंबंध का सिद्धांत अत्यंत उपयोगी है। इस सिद्धांत का विकास फ्रांसिस गाल्टन व कार्ल पियर्सन ने प्राणिशास्त्र तथा जनन-विद्या की अनेक समस्याओं के आधार पर किया था। अर्थशास्त्र में सहसंबंध के महत्त्व के बारे में नीसकेंजर लिखते हैं-“सहसंबंध विश्लेषण आर्थिक व्यवहार, को समझने में योग देता है, विशेष महत्त्वपूर्ण चरों जिन पर अन्य चर निर्भर करते हैं, को खोजने में सहायता देता है, अर्थशास्त्री को उन सुझावों को स्पष्ट करता है, जिससे गड़बड़ी फैलती है तथा उसे उन उपायों का सुझाव देता है जिनके द्वारा स्थिरता लाने वाली शक्तियाँ प्रभावित हो सकती हैं। सांख्यिकीय विधि के रूप में सहसंबंध के महत्त्व को निम्नलिखित प्रकार से स्पष्ट किया जा सकता है-

1. कारण एवं परिणाम में संबंध स्पष्ट करना- सहसंबंध वैज्ञानिक, सामाजिक तथा आर्थिक क्षेत्रों में दो या दो से अधिक घटनाओं के आपसी संबंधों को स्पष्ट करता है। यह स्पष्ट करता है कि विभिन्न समस्याओं के कारण और परिणाम में कितना और किस प्रकार का संबंध है।
2. नियमों तथा धारणाओं का निर्माण- सहसंबंध के अध्ययन से चरों के पारस्परिक संबंध की दिशा और मात्रा का ज्ञान होता है। जब यह विदित हुआ कि कीमत के बढ़ने पर माँग घट जाती है। और कीमत के घटने पर माँग बढ़ जाती है तब माँग के नियम का निर्माण हुआ।
3. नीति निर्माण में सहायक- सहसंबंध नीति निर्माण में सहायक होता है। कर की दर और कर संग्रह में ऋणात्मक संबंध होने पर सरकार कर की दरों को कम करती है। इसी प्रकार मुद्रा की पूर्ति एवं मुद्रा स्फीति की दर में धनात्मक सहसंबंध होने पर सरकार मुद्रा की पूर्ति को नियंत्रित करती है।
4. व्यापारिक निर्णय लेने में सहायक- संहसंबंध विश्लेषण व्यापारिक निर्णय लेने में सहायक होता है। इसका कारण यह है कि एक चर में परिवर्तन की प्रवृत्ति से दूसरे चरों में होने वाली प्रवृत्ति का पूर्वानुमान लगाया जा सकता है और इसी आधार पर व्यापारिक निर्णय लिए जाते हैं। माना जाता है कि सहसंबंध विश्लेषण पर आधारित अनुमान अधिक विश्वसनीय और निश्चित होते हैं।
टिप्पेट के शब्दों में- “सहसंबंध हमारी भविष्यवाणी की अनिश्चितता को कम करता है।”

सहसंबंध ज्ञात करने की रीतियाँ
सहसंबंध ज्ञात करने की प्रमुख रीतियाँ निम्नलिखित हैं-

(अ) बिन्दुरेखीय रीतियाँ|

• साधारण बिन्दुरेखीय रीति
• विक्षेप या बिन्दु चित्र रीति

(ब) गणितीय रीतियाँ

• कार्ल पियर्सन का सहसंबंध गुणांक
• स्पियरमैन की श्रेणी अंतर विधि।

प्रश्न 4.
सहसंबंध ज्ञात करने की साधारण बिन्दुरेखीय रीति की गणना प्रक्रिया को उदाहरण की सहायता से समझाइए।
उत्तर-
साधारण बिन्दुरेखीय रीति
इस रीति के अनुसार, ग्राफ पेपर पर दोनों चरों को बिन्दुओं के रूप में प्रकट किया जाता है। भुजाक्ष (X-axis) पर समय, स्थान आदि को लिया जाता है तथा कोटि-अक्ष (Y-axis) पर श्रेणी के मूल्यों को अंकित किया जाता है। प्राप्त बिन्दुओं को मिला देने से वक्र प्राप्त हो जाता है।

1. यदि दोनों रेखाएँ एक ही दिशा के साथ-साथ चलती हैं तो धनात्मक सहसंबंध होगा।
2. यदि दोनों रेखाएँ एक ही अनुपात में बढ़ती हैं तो उच्च स्तरीय धनात्मक सहसंबंध होगा।
3. यदि दोनों रेखाएँ दो विपरीत दिशाओं में उच्चावचन करती हैं तो ऋणात्मक सहसंबंध होगा।
4. यदि दोनों रेखाएँ समान गति से विपरीत दिशा में उच्चावचन करती हैं तो उच्च स्तरीय ऋणात्मक सहसंबंध होगा।
5. यदि रेखाओं में इस प्रकार की किसी प्रवृत्ति का आभास नहीं मिलता तो दोनों श्रेणियों में कोई संबंध नहीं होगा।
   उदाहरण- निम्नलिखित आँकड़ों से एक सहसंबंध रेखाचित्र बनाइए।

प्रश्न 5.
कार्ल पियर्सन के सहसंबंध गुणांक की गणना विधि उपयुक्त उदाहरणों की सहायता से समझाइए।
उत्तर-
कार्ल पियर्सन का सहसंबंध गुणांक यह सहसंबंध ज्ञात करने की सर्वोत्तम गणितीय रीति है। इस विधि द्वारा दिशा व मात्रा का अनुमान ही नहीं बल्कि उसका परिमाणात्मक माप भी प्राप्त होता है। यह गणितीय माध्य और प्रमाप विचलन पर आधारित है, इसलिए गणितीय दृष्टि से इसमें पूर्ण शुद्धता होती है।
मुख्य विशेषताएँ।

• यह रीति गणितीय दृष्टि से उपयुक्त है क्योंकि यह प्रमाप विचलन एवं समान्तर माध्य पर आधारित
• यह रीति बीजगणितीय दृष्टि से उत्तम है क्योंकि यह श्रेणी के सभी मूल्यों व पदों पर आधारित होती
• इस रीति से सहसंबंध की दिशा, मात्रा व सीमाओं का ज्ञान सुविधापूर्वक हो जाता है।
• यह सदैव +1 के मध्य रहता है।

कार्ल पियर्सन के सहसंबंध गुणांक का परिकलन
(I) व्यक्तिगत श्रेणी में प्रत्यक्ष रीति– व्यक्तिगत श्रेणी में प्रत्यक्ष रीति द्वारा सहसंबंध गुणांक निकालने की किँया इस प्रकार है-

प्रश्न 6.
स्पीयरमैन के कोटि सहसम्बन्ध गुणांक की गणना विधि को उदाहरणों की सहायता से समझाइए।
उत्तर-
स्पीयरमैन का कोटि सहसम्बन्ध गुणांक
गणना की दृष्टि से यह एक सरलतम विधि है क्योंकि यह श्रेणी के मूल्यों के क्रम (ranks) पर आधारित है। यह रीति ऐसी परिस्थितियों के लिए अधिक उपयुक्त है जहाँ तथ्यों का प्रत्यक्ष संख्यात्मक माप सम्भव न हो तथा उन्हें केवल एक निश्चित कोटि क्रम के अनुसार रखा जा सके। इस रीति द्वारा गणन प्रक्रिया निम्नलिखित प्रकार से है|

• फ्रत्येक श्रेणी में दिए गए व्यक्तिगत मूल्यों के सामने उनके क्रम लिखे जाते हैं। सबसे बड़ी संख्या को क्रम 1, उससे छोटी संख्या को क्रम 2, उससे छोटी संख्या को क्रम 3…………. आदि।
• दोनों श्रेणियों के क्रमों का अन्तर (D) निकाला जाता है।
• इस अन्तर का वर्ग (D²) करके उसका योग () ज्ञात किया जाता है।
• अन्त में निम्नलिखित सूत्र का प्रयोग किया जाता है-

We hope the UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 7 Correlation (सहसंबंध) help you. If you have any query regarding UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 7 Correlation (सहसंबंध), drop a comment below and we will get back to you at the earliest.