UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 4 Presentation of Data (आँकड़ों का प्रस्तुतीकरण)
पाठ्य-पुस्तक के प्रश्नोत्तर
निम्नलिखित 1 से 10 तक के प्रश्नों के सही उत्तर चुनें
प्रश्न 1.
दण्ड-आरेख|
(क) एकविमी आरेख है।
(ख) द्विविमी आरेख है।
(ग) विमारहित आरेख है।
(घ) इनमें से कोई नहीं
उत्तर :
(क) एकविमी आरेख है।
प्रश्न 2.
आयत चित्र के माध्यम से प्रस्तुत किए गए आँकड़ों से आलेखी रूप से निम्नलिखित जानकारी प्राप्त कर सकते हैं
(क) माध्य
(ख) बहुलक
(ग) मध्यिका
(घ) ये सभी
उत्तर :
(ग) मध्यिका
प्रश्न 3.
तोरणों के द्वारा आलेखी रूप में निम्न की स्थिति जानी जा सकती है|
(क) बेहुलक
(ख) माध्य
(ग) मध्यिका
(घ) इनमें से कोई नहीं
उत्तर :
(ग) मध्यिकी
प्रश्न 4.
अंकगणितीय रेखाचित्र के द्वारा प्रस्तुत आँकड़ों से निम्न को समझने में मदद मिलती है
(क) दीर्घकालिक प्रवृत्ति
(ख) आँकड़ों में चक्रीयता
(ग) आँकड़ों में कालिकता
(घ) ये सभी
उत्तर :
(क) दीर्घकालिक प्रवृत्ति
प्रश्न 5. दण्ड-आरेख के दण्डों की चौड़ाई का एकसमान होना जरूरी नहीं है। (सही/गलत)
उत्तर :
सही।
प्रश्न 6.
आयत चित्रों में आयतों की चौड़ाई अवश्य एकसमान होनी चाहिए। (सही/गलत)
उत्तर :
गलत।
प्रश्न 7.
आयत चित्र की रचना केवल आँकड़ों के संतत वर्गीकरण के लिए की जा सकती है। (सही/गलत)
उत्तर :
सही।
प्रश्न 8.
आयत चित्र एवं स्तम्भ आरेख आँकड़ों को प्रस्तुत करने के लिए एक जैसी विधियाँ हैं। (सही/गलत)
उत्तर :
सही।
प्रश्न 9.
आयत चित्र की मदद से बारम्बारता वितरण के बहुलक को आलेखी रूप में जाना जा सकता है। (सही/गलत)
उत्तर :
सही।
प्रश्न 10.
तोरणों से बारम्बारता वितरण की मध्यिका को नहीं जाना जा सकता है। (सही/गलत
उत्तर :
गलत।
प्रश्न 11.
निम्नलिखित को प्रस्तुत करने के लिए किस प्रकार का आरेख अधिक प्रभावी होता है?
(क) वर्ष-विशेष की मासिक वर्षा।
उत्तर :
वर्ष-विशेष की मासिक वर्षा को प्रस्तुत करने के लिए दण्ड-आरेख अधिक प्रभावी है क्योंकि यहाँ एक चर को ही प्रस्तुत करना है।
(ख) धर्म के अनुसार दिल्ली की जनसंख्या का संघटन।
उत्तर :
धर्म के अनुसार दिल्ली की जनसंख्या का संघटन प्रस्तुत करने के लिए सरल दण्ड आरेख ही अधिक उपयुक्त है। इसे अतिरिक्त घटक दण्ड आरेख भी बनाया जा सकता है।
(ग) एक कारखाने में लागत घटक।
उत्तर :
एक कारखाने में लागत घटक को प्रस्तुत करने के लिए बहुगुणी दण्ड आरेख अधिक प्रभावी है।
प्रश्न 12.
मान लीजिए आप भारत में शहरी गैर-कामगारों की संख्या में वृद्धि तथा भारत में शहरीकरण के निम्न स्तर पर बल देना चाहते हैं, जैसा कि उदाहरण 4.2 में दिखाया गया है। तो आप उसका सारणीयन कैसे करेंगे?
उत्तर :
भारत में शहरी कामगारों एवं गैर-कामगारों का हिस्सा

सारणी देखने से पता चलता है कि भारत में शहरी गैर-कामगार की संख्या अधिक है जो यह दर्शाता है। कि भारत में शहरीकरण निम्न स्तर का है।
प्रश्न 13.
यदि किसी बारम्बारता सारणी में समान वर्ग अन्तरालों की तुलना में वर्ग अन्तराल असमान हों, तो आयत चित्र बनाने की प्रक्रिया किस प्रकार भिन्न होगी?
उत्तर :
वर्ग अन्तराल के समान होने पर आयत चित्र का आधार एकसमान होता है। आयतों की तुलना संगत आवृत्ति के आधार पर की जाती है। किन्तु जब वर्ग अन्तराल असमान होते हैं तो सर्वप्रथम आयतों की ऊँचाइयों को समायोजित किया जाता है और फिर इनकी तुलना की जाती है। आयतों की ऊँचाइयों के समायोजन की प्रक्रिया है-आवृत्ति घनत्व को वर्ग अन्तराल की चौड़ाई से विभाजित करना। इसमें निरपेक्ष आवृत्तियों का प्रयोग नहीं किया जाता है।
प्रश्न 14.
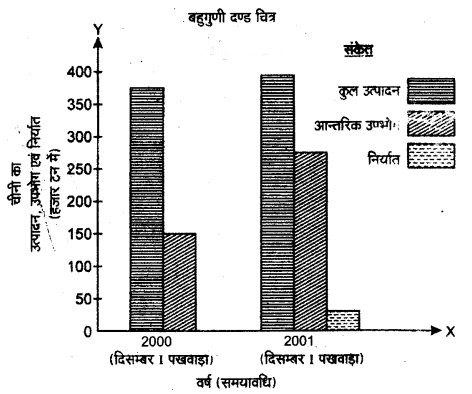
भारतीय चीनी कारखाना संघ की रिपोर्ट में कहा गया है कि दिसम्बर 2001 के पहले पखवाड़े के दौरान 38,77,000 टन चीनी का उत्पादन हुआ, जबकि ठीक इसी अवधि में पिछले वर्ष (2000 में) 37,87,000 टन चीनी का उत्पादन हुआ था। दिसम्बर 2001 में घरेलू खपत के लिए चीनी मिलों से 2,83,000 टन चीनी उठाई गई और 41,000 टन चीनी निर्यात के लिए थी, जबकि पिछले वर्ष की इसी अवधि में घरेलू खपत की मात्रा 1,54,000 टन थी और निर्यात शून्य था।
(क) उपर्युक्त आँकड़ों को सारणीबद्ध रूप में प्रस्तुत करें।
(ख) मान लीजिए आप इस आँकड़े को आरेख के रूप में प्रस्तुत करना चाहते हैं तो कौन-सा आरेख चुनेंगे और क्यों?
(ग) इन आँकड़ों को आरेखी रूप में प्रस्तुत करें।
उत्तर :
(क) शीर्षक – भारत में चीनी का उत्पादन, उपभोग व निर्यात

(ख) हम इन आँकड़ों को आरेख में प्रस्तुत करने के लिए बहुगुणी दण्ड चित्र का प्रयोग करेंगे। इस चित्र में हम अलग-अलग प्रकार के तथा अलग-अलग वर्षों के आँकड़ों को अधिक अच्छी तरह से दर्शा सकते हैं।
(ग) आरेख
प्रश्न 15.
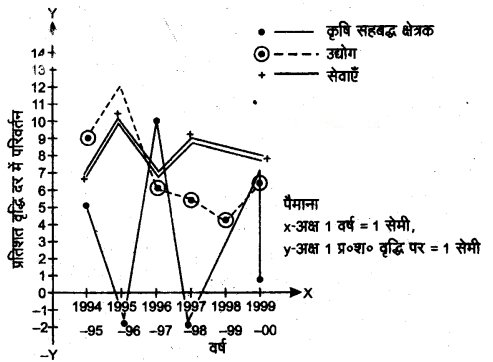
निम्नलिखित सारणी में कारक लागत पर सकल घरेलू उत्पाद में क्षेत्रकवार अनुमानित वास्तविक संवृद्धि दर को (पिछले वर्ष से प्रतिशत परिवर्तन) प्रस्तुत किया गया है|

उपर्युक्त आँकड़ों को बहु काल-श्रेणी आरेख द्वारा प्रस्तुत करें।
परीक्षोपयोगी प्रश्नोत्तर
बहुविकल्पीय प्रश्न
प्रश्न 1.
“एक सांख्यिकीय सारणी आँकड़ों का स्तम्भों तथा पंक्तियों में आँकड़ों का व्यवस्थित संगठन है।” यह परिभाषा किसने दी है?
(क) प्रो० मार्शल
(ख) प्रो० रोबिन्स
(ग) प्रो० नीसवेंजर
(घ) प्रो० कॉनर
उत्तर :
(ग) प्रो० नीसवेंजर
प्रश्न 2.
सारणीयन सांख्यिकीय विश्लेषण में ……………………………………………. है।
(क) सहायक
(ख) असहायक
(ग) कभी-कभी सहायक
(घ) (क) और (ख) दोनों
उत्तर :
(क) सहायक
प्रश्न 3.
एक अच्छी सांख्यिकीय श्रेणी का गुण नहीं है
(क) सारणी का आकार उचित एवं सन्तुलित होना चाहिए
(ख) तुलनात्मक समंकों को दूरवर्ती खानों में रखा जाना चाहिए
(ग) बड़ी संख्याओं का उपसादन कर लेना चाहिए।
(घ) प्रत्येक वर्ग तथा उपवर्ग का योग दिया जाना चाहिए
उत्तर :
(ख) तुलनात्मक समंकों को दूरवर्ती खानों में रखा जाना चाहिए।
प्रश्न 4.
इनमें से कौन नीरस समंकों को अर्थपूर्ण, रोचक व अधिक बोधगम्य बनाते हैं?
(क) शब्द
(ख) अंक
(ग) लेख
(घ) चित्र
उत्तर :
(घ) चित्र
प्रश्न 5.
किसमें एक ही प्रकार के संख्यात्मक तथ्यों के विभिन्न मूल्यों को दण्डों के द्वारा प्रकट किया जाता है?
(क) सरल दण्ड चित्र में
(ख) बहुगुणी दण्ड चित्र में
(ग) अन्तर्विभक्त दण्ड चित्र में
(घ) आवृत्ति आयत चित्र में
उत्तर :
(क) सरल दण्ड चित्र में
अतिलघु उत्तरीय प्रश्न
प्रश्न 1.
आँकड़ों के प्रस्तुतीकरण से क्या आशय है?
उत्तर :
आँकड़ों को स्पष्ट तथा व्यवस्थित रूप से इस प्रकार से प्रस्तुत करना कि उन्हें सभी व्यक्ति सरलतापूर्वक समझ सकें और उनसे उचित परिणाम निकाल सकें, आँकड़ों का प्रस्तुतीकरण कहलाता है।
प्रश्न 2.
पाठ्य प्रस्तुतीकरण से क्या आशय है?
उत्तर :
पाठ्य प्रस्तुतीकरण में आँकड़े अध्ययन की विषय-वस्तु के वर्णन का एक अंश होते हैं। इसे वर्णनात्मक प्रस्तुतीकरण भी कहते हैं।
प्रश्न 3.
पाठ्य प्रस्तुतीकरण किस दशा में उपयुक्त रहता है?
उत्तर :
पाठ्य प्रस्तुतीकरण तब उपयुक्त रहता है जब आँकड़ों की संख्या अधिक न हो तथा अध्ययन की विषय-वस्तु के रूप में आँकड़ों का आकार छोटा हो।
प्रश्न 4.
सारणीयन की परिभाषा दीजिए।
उत्तर :
सारणीयन आँकड़ों के सांख्यिकीय विश्लेषण की प्रक्रिया को वह भाग है, जिससे विभिन्न श्रेणियों में आने वाले आँकड़ों को गिना एवं दिखाया जाता है।
प्रश्न 5.
सारणीयन की दो उपयोगिता बताइए।
उत्तर :
- सारणीयम आँकड़ों को सुव्यवस्थित करता है।
- सारणीयन सांख्यिकीय विश्लेषण में सहायक है।
प्रश्न 6.
बहुगुणी सारणी किसे कहते हैं?
उत्तर :
जब किसी घटना अथवा तथ्य से सम्बन्धित तीन से अधिक गुणों एवं विशेषताओं का प्रदर्शन एक-साथ किया जाता है तो इसे ‘बहुगुणी सारणी’ कहा जाता है।
प्रश्न 7.
एकविमा चित्र से क्या आशय है?
उत्तर :
वे चित्र जिनके बनाने में केवल एक ही विस्तार अथवा ऊँचाई को (चौड़ाई अथवा मोटाई का नहीं) प्रयोग किया जाता है, एकविमा चित्र कहलाते हैं।
प्रश्न 8.
दण्ड चित्र क्या है?
उत्तर :
दण्ड चित्र वह चित्र है जिसमें आँकड़ों को दण्डों या आयतों के रूप में प्रकट किया जाता है।
प्रश्न 9.
बहुगुणी दण्ड चित्र क्या हैं?
उत्तर :
बहुगुणी दण्ड चित्र वे दण्ड चित्र हैं जो दो-या-दो से अधिक तथ्यों के आँकड़ों को प्रस्तुत करते हैं। प्रत्येक तथ्य के लिए अलग-अलग दण्ड चित्र बनाए जाते हैं। प्रत्येक दण्ड को भिन्न रंग या चिह्न द्वारा प्रदर्शित किया जाता है।
प्रश्न 10.
अन्तर्विभक्त दण्ड चित्र क्या है?
उत्तर :
अन्तर्विभक्त दण्ड चित्र वह चित्र है जो किसी तथ्य के कुल मूल्य तथा उपविभाजन को प्रस्तुत करता है। इसमें सम्पूर्ण मूल्य का एक दण्ड बनाकर उसका उपविभाजन कर दिया जाता है और दण्ड के | भिन्न-भिन्न भागों में भिन्न-भिन्न रंग भर दिए जाते हैं।
प्रश्न 11.
प्रतिशत दण्ड चित्र क्या है?
उत्तर :
प्रतिशत दण्ड चित्र प्रदर्शन की वह विधि है जिसमें किसी तथ्य के विभिन्न भागों के मूल्यों को प्रतिशत के रूप में दिखाया जाता है।
प्रश्न 12.
वृत्तीय चित्र से क्या आशय है?
उत्तर :
वृत्तीय चित्र वह चित्र है जिसमें एक वृत्त (circle) को कई भागों में बाँटकर आँकड़ों के भिन्न-भिन्न प्रतिशत या सापेक्ष मूल्यों को प्रस्तुत किया जाता है।
प्रश्न 13.
आयत चित्र क्या है?
उत्तर :
आयत चित्र वह रेखाचित्र है जिसमें अखण्डित श्रृंखला (continuous series) से सम्बन्धित मदों तथा उनकी आवृत्तियों को आयतों के रूप में ग्राफ पेपर पर अंकित किया जाता है।
प्रश्न 14.
आवृत्ति बहुभुज (Frequency Polygon) क्या है?
उत्तर :बहुभुज आयत चित्र के प्रत्येक आयत के शीर्ष के मध्य बिन्दुओं को सरल रेखाओं द्वारा मिलाकर बनाया जाता है।
प्रश्न 15.
आवृत्ति वक्र (Frequency Polygon) क्या है?
उत्तर :
आवृत्ति वक्र आवृत्ति बहुभुज को मुक्त हस्त रीति से खींचा हुआ सरल रूप है।
प्रश्न 16.
आवृत्ति बहुभुज तथा आवृत्ति वक्र में क्या अन्तर है?
उत्तर :
आवृत्ति बहुभुज में मध्य बिन्दुओं को एक पैमाने की सहायता से मिलाया जाता है जबकि आवृत्ति वक्र में बिन्दुओं को मुक्त हस्त रीति द्वारा खींची जाने वाली रेखाओं द्वारा मिलाया जाता है।
प्रश्न 17.
तोरण अथवा ओजाइव अथवा संचयी आवृत्ति वक्र से क्या आशय है?
उत्तर :
तोरण अथर्वा संचयी आवृत्ति वक्र (Ogive) वह वक्र है जो ग्राफ पेपर पर संचयी आवृत्तियों को अंकित करके बनाया जाता है।
प्रश्न 18.
चित्रों की दो सीमाएँ बताइए।
उत्तर :
- चित्रों द्वारा यथार्थ संख्यात्मक प्रदर्शन सम्भव नहीं है। वे सन्निकट मूल्यों पर आधारित होते हैं।
- चित्रों की सहायता से विभिन्न मूल्यों का सूक्ष्म अन्तर प्रदर्शित करना असम्भव है।
लघु उत्तरीय प्रश्न
प्रश्न 1.
आँकड़ों के पाठ-विषयक प्रस्तुतीकरण पर एक नोट लिखिए।
उत्तर :
आँकड़ों के पाठ-विषयक प्रस्तुतीकरण में आँकड़ों का विवरण पाठ में ही दिया जाता है। जब आँकड़ों का परिमाण बहुत अधिक न हो तो प्रस्तुतीकरण का यह स्वरूप अधिक उपयोगी होता है। उदाहरण-उत्तर प्रदेश के एक शहर मेरठ में 5 सितम्बर, 2006 को महँगाई के विरोध में एक बन्द आयोजित किया गया। इस दौरान 6 बाजार खुले तथा 28 बाजार बन्द पाए गए। 25 प्राथमिक विद्यालय खुले किन्तु 17 माध्यमिक विद्यालय, 7 महाविद्यालय बन्द रहे। उपयुक्तता—यह विधि उस समय उपयुक्त होती है जब आँकड़े संख्या में कम और आकार में सीमित हों। दोष—इसे समझने के लिए पूरे पाठ का अध्ययन आवश्यक है। पढ़ते समय महत्त्वपूर्ण बिन्दु छूट सकते
प्रश्न 2.
सारणीयन में प्रयुक्त वर्गीकरण के प्रकार बताइए।
उत्तर :
सारणीयन में प्रयुक्त वर्गीकरण के चार प्रकार होते हैं
- गुणात्मक वर्गीकरण-जब वर्गीकरण गुणात्मक विशेषताओं के आधार पर किया जाए; जैसे–सामाजिक स्थिति, राष्ट्रीयता आदि।
- मात्रात्मक वर्गीकरण-जब वर्गीकरण उन विशेषताओं के आधार पर किया जाए जिन्हें मापा जा सकता है; जैसे—आयु, लम्बाई, उत्पादन, आय आदि।।
- कालिक वर्गीकरण-जब वर्गीकरण समय के आधार पर किया जाए; जैसे-घण्टे, दिन, सप्ताह, माह, वर्ष आदि।
- स्थानिक वर्गीकरण–जब वर्गीकरण स्थान के आधार पर किया जाए; जैसे–गाँव, कस्बा, जिला, राज्य, देश आदि।
प्रश्न 3.
चित्रमय प्रदर्शन की प्रमुख सीमाएँ बताइए।
उत्तर :
चित्रमय प्रदर्शन की प्रमुख सीमाएँ निम्नलिखित हैं
- चित्रों की उपयोगिता सामान्य व्यक्ति के लिए है, किसी विशेषज्ञ के लिए नहीं।
- चित्रों के माध्यम से विभिन्न मूल्यों का सूक्ष्म अन्तर प्रदर्शित करना सम्भव नहीं होता।
- चित्र अनेक प्रकार की तुलना करने में अनुपयोगी होते हैं।
- जब मापों के मध्य विशाल अन्तर होता है तो उस अन्तर को चित्रों द्वारा प्रदर्शित करना कठिन हो जाता है।
- चित्रों का और अधिक निर्वचन करना सम्भव नहीं होता।
- गलत मापदण्ड पर बने चित्र भ्रामक होते हैं।
- चित्र निष्कर्ष निकालने का केवलएक साधन हैं; अत: इनका प्रयोग सारणियों के साथ किया जाना चाहिए। :
- सन्निकट मूल्यों पर आधारित होने के कारण चित्र तथ्यों का यथार्थ प्रदर्शन नहीं कर पाते।
- तुलनात्मक अध्ययन के लिए समंकों का सजातीय होना आवश्यक है।
प्रश्न 4.
बहुगुणी दण्ड चित्र की उदाहरण सहित निर्माण विधि समझाइए।
उत्तर :
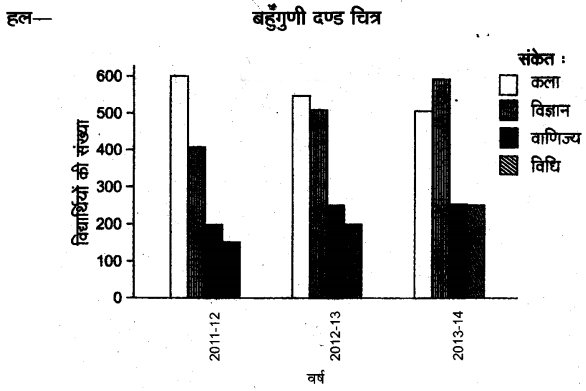
बहुगुणीय दण्ड चित्र-जब दो-या-दो से अधिक सम्बन्धित तथ्यों की समय या स्थान के आधार पर तुलना करनी होती है, तब बहुगुणी दण्ड चित्रों का निर्माण किया जाता है। इसमें एक स्थान या समय से सम्बन्धित विभिन्न तथ्यों के दण्डों को एक-दूसरे से मिलाकर बनाया जाता है तथा थोड़ा स्थान छोड़कर दूसरे स्थान या समय से सम्बन्धित विभिन्न तथ्यों के दण्ड को एक-दूसरे से मिलाकर बनाया जाता है। इस प्रकार दिए गए सभी स्थानों या समय हेतु समान अन्तर पर संयुक्त दण्ड बना लिए जाते हैं। इन्हें बहुगुणीय दण्ड चित्र कहा जाता है। विभिन्न तथ्यों को प्रदर्शित करने वाले दण्डों को भिन्न-भिन्न रंगों या डिजाइनों द्वारा दर्शाया जाता है।
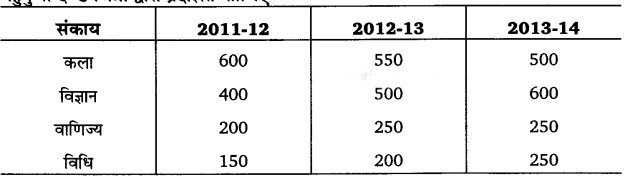
उदाहरण-एक कॉलेज के चार संकायों की छात्र संख्या में तीन वर्षों में होने वाले परिवर्तनों को बहुगुणी दण्ड चित्रों द्वारा प्रदर्शित कीजिए
प्रश्न 5.
प्रतिशत अन्तर्विभक्त दण्ड चित्र के निर्माण की प्रक्रिया को उदाहरण सहित समझाइए।
उत्तर :
प्रतिशत अन्तर्विभक्त दण्ड चित्र-इन चित्रों का निर्माण प्रायः उस समय किया जाता है जब हमें विभिन्न दण्डों के उपविभागों की सापेक्ष तुलना करनी होती है। इसके निर्माण के लिए सर्वप्रथम प्रत्येक तथ्य या वर्ग या समूह से सम्बन्धित विभिन्न उपविभागों के समंकों को जोड़कर उसे 100 मान लिया जाता है तथा प्रत्येक उपविभाग के प्रतिशत ज्ञात कर लिए जाते हैं। तत्पश्चात् संचयी प्रतिशत ज्ञात कर अन्तर्विभक्त दण्ड चित्रों के अनुसार आरेख का निर्माण किया जाता है।
उदाहरण – परिवार ‘A’ और ‘B’ के सदस्यों के विवरण को अन्तर्विभक्त प्रतिशत दण्ड चित्र द्वारा दर्शाइए
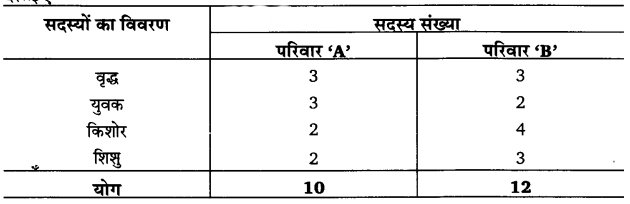
अन्तर्विभक्त प्रतिशत दण्ड चित्र बनाने के लिए पहले उपर्युक्त आँकड़ों को प्रतिशत में परिवर्तित करना पड़ता है।
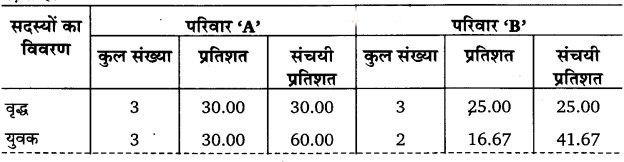

परिवार ‘A’ और ‘B’ के सदस्यों का अन्तर्विभक्त प्रतिशत दण्ड चित्र द्वारा प्रदर्शन

प्रश्न 6.
अन्तर्विभक्त दण्ड चित्र का निर्माण कैसे किया जाता है? उदाहरण दीजिए
उत्तर :
अन्तर्विभक्त दण्ड चित्र–अन्तर्विभक्त दण्ड चित्रों का निर्माण तब किया जाता है जब ऐसे तथ्यों की परस्पर तुलना करनी होती है जो कई भागों में विभक्त हैं। इनका निर्माण करने के लिए एक तथ्य या वर्ग या समूह से सम्बन्धित विभिन्न उपविभागों के समंकों को जोड़कर सर्वप्रथम सरल दण्ड चित्र बना लिए जाते। हैं। तत्पश्चात् प्रत्येक दण्ड को उसके उपविभागों के मूल्य के अनुसार विभक्त कर देते हैं। प्रत्येक उपविभाग के लिए अलग-अलग रंग, आभा या छाया का प्रयोग किया जाता है।
उदाहरण – एक कॉलेज के चार संकायों की छात्र संख्या में तीन वर्षों में होने वाले परिवर्तनों को अन्तर्विभक्त दण्ड चित्रों द्वारा प्रदर्शित कीजिए
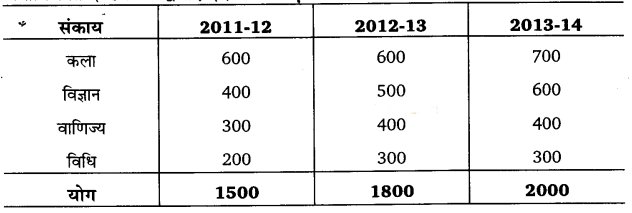
हल :
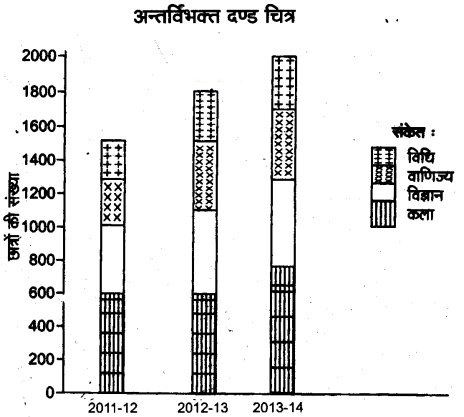
प्रश्न 7.
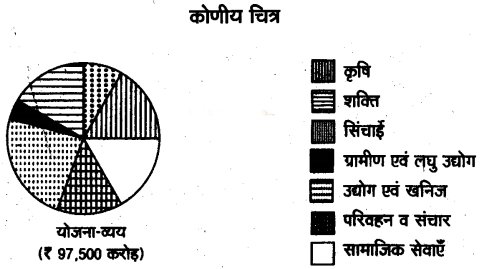
कोणीय अथवा वृत्त खण्ड चित्र के निर्माण की विधि उदाहरण सहित समझाइए।
उत्तर :
कोणीय अथवा वृत्तखण्ड चित्रकोणीय अथवा वृत्तखण्ड चित्रे वह चित्र है जिसमें एक वृत्त को अनेक उपविभागों में बाँटेकर आँकड़ों के भिन्न-भिन्न प्रतिशत या सापेक्ष मूल्यों को प्रदर्शित किया जाता है। वृत्त खण्ड चित्र बनाने के प्रमुख चरण निम्नलिखित हैं
- सर्वप्रथम किसी श्रृंखला के निरपेक्ष मूल्यों को प्रतिशत मूल्यों में बदला जाता है।
- एक वृत्त के चार कोण होते हैं। प्रत्येक कोण 90° का होता है। प्रत्येक वृत्त में कोणों का जोड़ 90° x 4 = 360° होता है।
- किसी आँकड़े से सम्बन्धित विभिन्न मूल्यों को 360° अंश के विभिन्न भागों में प्रस्तुत किया जाता है। प्रत्येक भाग का अंश निकालने के लिए उसके मूल्य को 360° से गुणा करके 100 से भाग कर दिया जाता है।
- प्रत्येक मूल्य को वृत्त में घड़ी की सुई की दिशा के अनुसार प्रकट किया जाता है।
उदाहरण – निम्नलिखित समंकों को कोणीय चित्र द्वारा निरूपित कीजिए

हल :

प्रश्न 8.
आयत चित्र का निर्माण कैसे किया जाता है? एक समान वर्गान्तर वाला आयतचित्र बनाइए।
उत्तर :
आयत चित्र-आयत चित्र में श्रृंखला के मदों एवं उनकी आवृत्तियों को आयतों के रूप में प्रदर्शित किया जाता है। इसमें वर्गान्तर को Ox अक्ष पर तथा आवृत्तियों को OY अक्ष पर प्रकट किया जाता है। ऑयतों की ऊँचाई आवृत्तियों के अनुपात में रखी जाती है। प्रत्येक वर्गान्तर की सीमाओं के माप बिन्दुओं पर आवृत्ति की ऊँचाई के बराबर लम्बी रेखाएँ खींचकर आयत बना लिए जाते हैं। आयत एक-दूसरे से मिले हुए। रहते हैं। यदि श्रेणी समावेशी है तो उसे अपवर्जी बना लेते हैं। उदाहरण—निम्नांकित समंकों को आवृत्ति आयत चित्र द्वारा प्रदर्शित कीजिए और बहुलक का मूल्य निकालिए।
वर्गान्तर : 0-10 10-20 20-30 30-40 40-50 50-60 60-70
आवृत्ति : 4 8 14 20 30 15 6

प्रश्न 9.
एक काल्पनिक उदाहरण की सहायता से असमान वर्गान्तर वाला आयत चित्र बनाइए।
उत्तर :
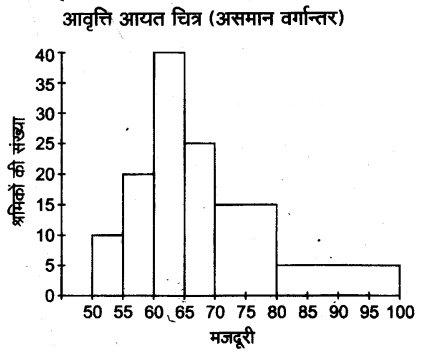
यदि वर्गान्तर असमान है तो आवृत्तियों को सर्वप्रथम समायोजित किया जाता है। इसे उदाहरण के बाद समझाया गया हैउदाहरण
मजदूरी : 50-55 55-60 60-65 65-70 70-80 80-100
श्रमिकों की संख्या : 10 18 40 25 32 24
उपर्युक्त उदाहरण में वर्गान्तर असमान है। आवृत्ति वितरण में न्यूनतम वर्गान्तर 5 का है जबकि बाद में ये वर्गान्तर क्रमशः 10 व 20 हैं। इसलिए आवृत्ति चित्र बनाने से पहले आवृत्ति घनत्व की रचना की जाएगी। आवृत्तियों को समायोजित तत्त्व से भाग देने पर जो संख्या आती है, उसे आवृत्ति घनत्व कहा जाता है। अर्थात्,

समायोजित तालिका इस प्रकार होगी—

उपर्युक्त तालिका में पहले चार का वर्गान्तर 5 है। पाँचवें का 80 -70 = 10 है। यह न्यूनतम वर्गान्तर 5 से दुगुना है। अतः इसकी मदों को दो से भाग किया जाएगा। छठे का वर्गान्तर 100 – 80 = 20 है जो न्यूनतम वर्गान्तर से चार गुणा अधिक है। अतः इसकी मदों को चार से भाग किया जाएगा। उपर्युक्त तालिका के आधार पर आवृत्ति चित्र इस प्रकार बनेगा
प्रश्न 10.
आवृत्ति बहुभुज (frequency polygon) क्या है? एक काल्पनिक तालिका की सहायता से आवृत्ति बहुभुज की रचना कीजिए।
उत्तर :
आवृत्ति बहुभुज-आयत चित्र के प्रत्येक आयत के शीर्ष के मध्य बिन्दुओं को सरल रेखाओं द्वारा मिलाकर आवृत्ति ब्रहुभुज बनाया जाता है। इसके लिए प्रत्येक वर्ग के मध्य बिन्दु के मूल्य को ग्राफ पेपर पर अंकित कर लिया जाता है। इसके पश्चात् इन बिन्दुओं को सरल रेखाओं द्वारा मिला दिया जाता है। इसके फलस्वरूप जो रेखाचित्र बनता है, उसे आवृत्ति बहुभुज (frequency polygon) कहते हैं। उदाहरण—निम्नलिखित तालिका में कक्षा 11 के विद्यार्थियों के अर्थशास्त्र के प्राप्तांक दिए हुए हैं। इन्हें आवृत्ति बहुभुज द्वारा दर्शाइए
प्राप्तांक: 0-10 10-20 20-30 30-40 40-50 50-60 60-70
विद्यार्थियों की संख्या : 5 10 15 20 12 8 5
हल :

प्रश्न 11.
ओजाइव या संचयी आवृत्ति वक्र अथवा तोरण किसे कहते हैं? इसकी निर्माण प्रक्रिया क्य है? काल्पनिक उदाहरण की सहायता से संचयी आवृत्ति वक्र बनाइए।
उत्तर :
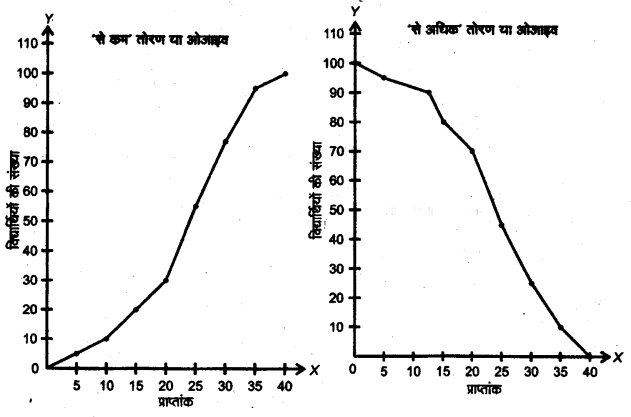
संचयी आवृत्ति वक्र—ओजाइव या संचयी आवृत्ति वक्र वह वक्र है जो ग्राफ पेपर पर संचयी आवृत्तियों को अंकित करके बनाया जाता है। इसकी रचना की दो विधियाँ हैं
- ‘से कम विधि (Less than Method)-इस विधि में हम निचली सीमाओं से आरम्भ करते हैं। और आवृत्तियों को जोड़ते जाते हैं।
- ‘से अधिक विधि (More than Method)—इस विधि में हम ऊपरी सीमाओं से आरम्भ करके
आवृत्ति को घटाते जाते हैं। उदाहरण-निम्नांकित तालिका में 11वीं कक्षा के विद्यार्थियों के ‘सांख्यिकी’ में प्राप्त अंकों का विवरण दिया हुआ है। इसके आधार पर ‘से कम’ ओजाइव एवं ‘से अधिक’ ओजाइव ( तोरण)
बनाइएप्राप्तांक: 0-5 5-10 10-15 15-20 20-25 25-30 30-35 35-40
विद्यार्थियों की संख्या : 4 6 10 10 25 22 18 5
हल :
सर्वप्रथम ‘से कम’ और ‘से अधिक आधार पर संचयी आवृत्ति बनाई जाएगी।

प्रश्न 12.
निम्नांकित सारणी में भारत में गत् 8 वर्षों के कच्चे लोहे के उत्पादन को दर्शाया गया है।
समंकों को उपयुक्त रेखाचित्र द्वारा प्रदर्शित कजिए
वर्ष : 2009 2010 2011 2012 2013 2014 2015 2016
उत्पादन (000 टन) : 19 21 25 48 67 76 90 97
हल :

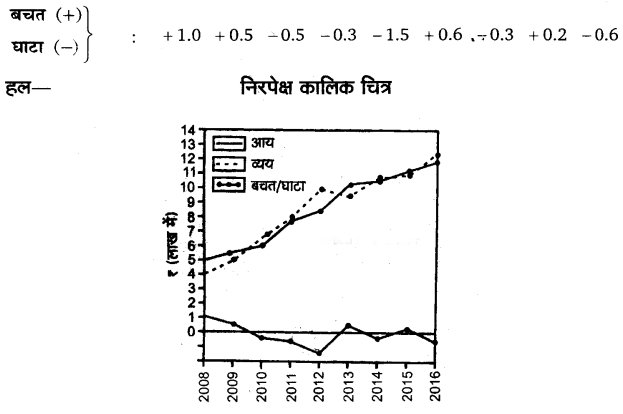
प्रश्न 13.
एक नगरपालिका के आय-व्यय और बचत/घाटे के निम्नांकित समंकों को बिन्दुरेखीय
चित्र द्वारा प्रदर्शित कीजिए
वर्ष : 2008 2009 2010 2011 2012 2013 2014 2015 2016
आय ₹ दस लाख : 5.0 5.5 6.0 7.7 8.5 10.2 10.6 11.2 12.0
व्यय ₹ दस लाख : 4.0 5.0 6.5 8.0 10.0 9.6 10.9 11.0 12.6
दीर्घ उत्तरीय प्रश्न
प्रश्न 1.
सारणीयन का अर्थ बताइए। इसके उद्देश्य, उपयोगिता एवं सीमाओं को स्पष्ट कीजिए।
उत्तर :
सारणीयन : अर्थ एवं परिभाषा आँकड़ों को एकत्र कोर लेने के पश्चात् उन्हें एक तार्किक क्रम में रखा जाता है। इस प्रक्रिया को सारणीयन कहा जाता है। सारणीयन में वर्गीकृत आँकड़ों को कॉलमों या स्तम्भों एवं पंक्तियों में दिखाया जाता है। इसको निम्नलिखित प्रकार से परिभाषित किया गया है–
- प्रो० नीसवेंजर के अनुसार – “एक सांख्यिकीय सारणी आँकड़ों का स्तम्भों (कॉलम) तथा पंक्तियों में आँकड़ों का व्यवस्थित संगठन है।”
- प्रो० कॉनर के अनुसार – “सारणीयन किसी विचाराधीन समस्या को स्पष्ट करने के उद्देश्य से किया जाने वाला सांख्यिकीय तथ्यों का क्रमबद्ध एवं सुव्यवस्थित प्रस्तुतीकरण है।”
सारणीयन के उद्देश्य
सारणीयन के प्रमुख उद्देश्य निम्नलिखित हैं
- आँकड़ों को सुव्यवस्थित बनाना – सारणीयन का प्रमुख उद्देश्य एकत्रित सामग्री का वर्गीकरण , कर लेने के पश्चात् इसे अधिक व्यवस्थित रूप प्रदान करना है ताकि निर्वचन की प्रक्रिया सरल हो सके।
- आँकड़ों को बोधगम्य बनाना – सारणीयन का दूसरा प्रमुख उद्देश्य आँकड़ों को सरल रूप से कॉलमों एवं कतारों में दिखाकर इन्हें अधिक बोधगम्य बनाना है।
- आँकड़ों की विशेषताओं को स्पष्ट करना – सारणी का एक प्रमुख उद्देश्य एकत्रित आँकड़ों की विविध प्रकार की विशेषताओं को प्रदर्शित करना है।
- आँकड़ों का संक्षिप्तीकरण करना – सारणीयन का एक महत्त्वपूर्ण उद्देश्य विस्तृत सामग्री का कम-से-कम स्थान पर प्रदर्शन करना है।
- आँकड़ों को तुलना योग्य बनाना – सारणीयन का अन्तिम उद्देश्य आँकड़ों की तुलना करने में सहायता देना है।
सारणीयन की उपयोगिता
सारणीयन की उपयोगिता को निम्नलिखित बिन्दुओं द्वारा स्पष्ट किया जा सकता है
- सारणीयन आँकड़ों को सुव्यवस्थित करता है।
- सारणीयन विस्तृत आँकड़ों को संक्षिप्त रूप प्रदान करता है।
- सारणीयन तुलना को सरल बनाता है।
- सारणीयन सांख्यिकीय विश्लेषण में सहायक है।।
- सारणीयन में न केवल समय व श्रम की बचत होती है अपितु उसमें स्पष्टता आ जाती है।
- सारणीयन सांख्यिकीय गणनाओं व विश्लेषण में सहायक होता है।
- सारणीबद्ध समंकों का निर्वचन करना व रेखाचित्रों द्वारा प्रदर्शित करना सरल एवं सुविधाजनक हो जाता है।
सारणीयन की सीमाएँ
सारणीयन की प्रमुख सीमाएँ निम्नलिखित हैं
- सारणीयन द्वारा केवल गणनात्मक आँकड़ों का ही प्रदर्शन किया जा सकता है, गुणात्मक तथ्यों का नहीं।
- सारणीयन द्वारा जिन आँकड़ों का प्रदर्शन किया जाता है, उन्हें सामान्य व्यक्तियों द्वारा समझने में कठिनाई हो सकती है। वास्तव में, इसका उपयोग केवल विशिष्ट एवं उच्च ज्ञान वाले व्यक्तियों तक ही सीमित है।
- सारणीयन का महत्त्व सीमित है क्योंकि एक सारणी में सम्पूर्ण सामग्री का प्रदर्शन नहीं किया जा सकता।
प्रश्न 2.
सारणी के विभिन्न प्रकारों को बताइए। सरल सारणी व जटिल सारणी के उदाहरण दीजिए।
उत्तर :
सारणी के प्रकार
सांख्यिकीय सामग्री का वर्गीकरण निम्नलिखित प्रकार से किया जा सकता है
(अ) उद्देश्य के आधार पर सारणीयन – उद्देश्य के आधार पर सारणियाँ दो प्रकार की होती हैं
1. सामान्य उद्देश्य वाली सारणी – क्रॉक्सटन व काउडेन के शब्दों में – “सामान्य उद्देश्य वाली सारणी का सबसे पहला और सामान्यत: एकमात्र उद्देश्य समंकों को इस प्रकार रखना होता है कि व्यक्तिगत पद पाठक द्वारा शीघ्र हूँढ़े जा सकें।” अत्यधिक विस्तृत होने के कारण यह सारणी अधिक उपयुक्त नहीं समझी जाती।
2. विशेष उद्देश्य वाली अथवा संक्षिप्त सारणी – यह किसी उद्देश्य विशेष की पूर्ति के लिए तैयार की जाती है और इसका आकार सामान्य सारणी से छोटा होता है।
(ब) रचना के आधार पर सारणीयन – रचना के आधार पर सारणियाँ निम्नलिखित दो प्रकार की हो सकती हैं–
1. सरल सारणी – सरल सारणी में समंकों को केवल एक ही गुण अथवा विशेषता के आधार पर प्रस्तुत किया जाता है। इस प्रकार की सारणी के केवल दो ही भाग होते हैं। उदाहरणार्थ

2. जटिल सारणी – जब समंकों को एक से अधिक विशेषताओं के आधार पर प्रस्तुत किया जाता है। तो वह ‘जटिल सारणी’ कहलाती है। जटिल सारणी निम्नलिखित प्रकार की हो सकती है
(i) द्विगुणीय सारणी – इस सारणी में दो परस्पर सम्बन्धित गुणों अथवा लक्षणों का प्रदर्शन एक साथ किया जाता है। उदाहरणार्थ

(ii) त्रिगुणीय सारणी – इस सारणी में किसी घटना अथवा तथ्य से सम्बन्धित तीन विशेषताओं का एक साथ प्रदर्शन किया जाता है। उदाहरणार्थ
त्रिगुणीय सारणी
2015-16 में ग्यारहवीं कक्षा के छात्रों के लिंग एवं वैवाहिक
स्तर के आधार पर सांख्यिकी’ में प्राप्तांक

(iii) बहुगुणीय सारणी – जब किसी घटना अथवा तथ्य से सम्बन्धित तीन से अधिक गुणों:एथें विशेषताओं का प्रदर्शन एक साथ किया जाता है तो इसे ‘बहुगुणी सारणी’ कहा जाता है। उदाहरणार्थ
बहुगुणीय सारणी
2015-16 में ग्यारहवीं कक्षा के छात्रों के लिंग एवं वैवाहिक स्तर के
आधार पर सांख्यिकी’ में प्राप्तांक कॉलेज प्राप्तांक
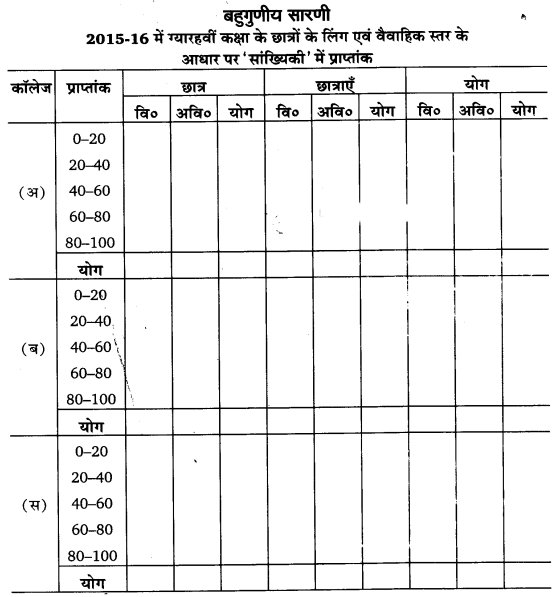
प्रश्न 3.
सारणी का निर्माण करते समय क्या-क्या सावधानियाँ बरतनी चाहिए? इसके सामान्य नियम क्या हैं?
उत्तर :
सारणी का निर्माण करते समय सावधानियाँ किसी भी सारणी का निर्माण करते समय निम्नलिखित सावधानियाँ बरतनी चाहिए
- शीर्षक (Heading)—प्रत्येक सारणी का संक्षिप्त, स्पष्ट एवं पूर्ण शीर्षक होना चाहिए।
- स्तम्भ अथवा कॉलम (Columns)—सारणी का निर्माण करते समय स्तम्भों के आकार व संख्या का ध्यान रखना चाहिए। स्तम्भ अधिक नहीं होने चाहिए तथा इनका आकार समान अनुपात में तथा समान आधार पर निश्चित किया जाना चाहिए।
- अनुशीर्षक (Captions)-अनुशीर्षक संक्षिप्त एवं स्पष्ट होना चाहिए।
- कतारें अथवा पंक्तियाँ (Rows)-क्षैतिज रेखाओं द्वारा बने खानों को ‘कतारे” कहा ज़ात है। कतारों में सूचना का आधार आँकड़ों का कोई भी गुण हो सकता है।
- स्तम्भों का क्रम (Sequence of Columns)-स्तम्भों का क्रम सोच-समझकर निर्धारित करना चाहिए। सर्वाधिक महत्त्व की सूचनाएँ बायीं ओर के स्तम्भों से शुरू की जानी चाहिए। तुलना किए जाने वाले स्तम्भों को साथ-साथ रखा जाना चाहिए।
- टिप्पणियाँ (Notes)-यदि सारणी में दिए गए तथ्यों के बारे में विशेष सूचना देना आवश्यक हो और उसका प्रदर्शन सम्भव न हो तो सारणी में दिखाए गए आँकड़ों पर कोई संकेत जैसे * या + आदि देकर नीचे इसी प्रकार का संकेत बनाकर टिप्पणी लिखी जाती है।
- खानों की रूलिंग (Ruling of Columns)-विषय-सामग्री का महत्त्वपूर्ण भाग मोटी या दोहरी रेखाओं से बनाया जाना चाहिए।
- योग (Total)–विभिन्न खानों की संख्याओं का योग दिया जाना चाहिए। योग की व्यवस्था दोनों ओर से होनी चाहिए।
- स्रोत (Source)-सारणी के नीचे समंकों का स्रोत स्पष्ट किया जाना चाहिए।
- सामान्य नियम-
- सारणी में अत्यधिक तथ्यों का समावेश नहीं होना चाहिए।
- संख्याओं को उपसादित करने के बाद ही लिखा जाना चाहिए। इस सम्बन्ध में आवश्यक टिपपणी भी दी जानी चाहिए।
- सारणी उपलब्ध स्थान के अनुसार ही नियोजित की जानी चाहिए।
- तुलनात्मक समंकों को निकटवर्ती खानों में रखा जाना चाहिए।
- साप की इकाई को स्पष्ट रूप से प्रदर्शित किया जाना चाहिए।
- अनुमानित अथवा उपलब्ध न होने वाली संख्याओं के सम्बन्ध में टिप्पणी देनी चाहिए।
- सारणी का रूप आकर्षक होना चाहिए।
- संख्याओं को लिखते समय उनके स्थानीय मान को ध्यान में रखना चाहिए।
प्रश्न 4.
एक अच्छी सांख्यिकीय श्रेणी के गुण बताइए।
उत्तर :
एक अच्छी सांख्यिकीय श्रेणी के गुण
एक अच्छी सांख्यिकीय श्रेणी (उत्तम सारणी) में निम्नलिखित गुण होने चाहिए
- सारणी का आकार उचित एवं सन्तुलित होना चाहिए।
- तुलनात्मक समंकों को निकटवर्ती खानों में रखा जाना चाहिए।
- अनुपात, प्रतिशत आदि को मूल समंकों के निकट ही लिखा जाना चाहिए और उनके गणनात्मक आधार पर संकेत दिए जाने चाहिए।
- बड़ी संख्याओं का उपसादन कर लेना चाहिए।
- प्रत्येक वर्ग तथा उपवर्ग का योग दिया जाना चाहिए।
- प्रत्येक सारणी के ऊपर संक्षिप्त, स्पष्ट तथा स्वयं परिचायक शीर्षक होना चाहिए।
- उपशीर्ष और अनुशीर्ष सूक्ष्म, स्पष्ट व स्वयं परिचायक होने चाहिए।
- सारणी में पदों की उचित व्यवस्था होनी चाहिए। पदों में क्रमबद्धता होनी चाहिए।
- प्रत्येक सारणी की संख्या सारणी के सबसे ऊपर दी जानी चाहिए।
- मोटी तथा पतली रेखाओं के प्रयोग से विभिन्न खानों के तथ्यों को प्रदर्शित किया जाना चाहिए।
- अनुमानित संख्याओं व उपलब्ध न होने वाली संख्याओं के सम्बन्ध में टिप्पणी दी जानी चाहिए।
- समंकों अथवा शब्दों को अधिक स्पष्ट करने के लिए सारणी के नीचे संक्षिप्त टिप्पणियाँ दी जानी चाहिए।
- सारणी के ऊपर एक किनारे पर या एक खाने में माप की इकाई को अवश्य लिखना चाहिए।
- गणन क्रिया का संकेत जैसे (col. 1 + col. 2) आदि दिए जाने चाहिए।’
- सारणी उपलब्ध स्थाने के अनुसार नियोजित की जानी चाहिए।
- सांख्यिकी में अत्यधिक तथ्यों को समावेश नहीं करना चाहिए।
- सारणी के नीचे वह स्रोत दिया जाना चाहिए जहाँ से समंक उपलब्ध किए गए हैं।
- सारणी का रूप आकर्षक होना चाहिए।
प्रश्न 5.
सांख्यिकी में चित्रों की आवश्यकता एवं महत्त्व को स्पष्ट कीजिए।
उत्तर :
सांख्यिकी विज्ञान का एक प्रमुख कार्य विशाल व जटिल समंक समूहों को इस प्रकार प्रस्तुत करना है कि वे सरल, स्पष्ट एवं समझने योग्य हो जाएँ। इस कार्य के लिए अनेक सांख्यिकीय विधियों का प्रयोग किया जाता है। इसमें समंकों का चित्रमय प्रदर्शन एक महत्त्वपूर्ण विधि है। चित्र नीरस समंकों को अर्थपूर्ण, रोचक व अधिक बोधगम्य बनाते हैं। चित्रमय प्रदर्शन की आवश्यकता, महत्त्व अथवा उपयोगिता को निम्न प्रकार स्पष्ट किया जा सकता है
1. आकर्षक एवं प्रभावी – चित्र आकर्षक होते हैं तथा मानव मस्तिष्क पर स्थायी प्रभाव डालते हैं। सामान्य व्यक्ति जो समंकों के जाल में उलझना नहीं चाहता चित्रों का रुचि के साथ अवलोकन करता है।
2. तथ्यों को सरल व बोधगम्य बनाना – चित्र जटिल एवं अव्यवस्थित विशाल तथ्यों को सरल वे सुबोध बनाते हैं। चित्रों के माध्यम से समंकों की समस्त विशेषताएँ स्पष्ट हो जाती हैं। प्रो० स्टीफन कल्फ के शब्दों में–“एक चित्र अधिक स्पष्ट तथा चित्त को सीधे किर्षित करने वाली तस्वीर प्रदान करता है।”
3. तुलना में सहायक – चित्रों से विभिन्न समंक समूहों में तुलना करना सरल हो जाता है। चित्रमय प्रदर्शन का एक प्रमुख उद्देश्य समंकों को तुलनीय बनाना है।
4. समय व श्रम की बचत – चित्रों द्वारा प्रदर्शित समंकों को बिना मस्तिष्क पर अधिक भार डाले ही सरलता से समझा जा सकता है। इससे समय व श्रम की बचत होती है।
5. व्यापक उपयोगिता – समंकों के चित्रमय प्रदर्शन का व्यापक प्रयोग होता है। आर्थिक, व्यापारिक, शासकीय, सामाजिक तथा अन्य क्षेत्रों में समंकों का व्यापक रूप से उपयोग होता है।
6. विशेष ज्ञान व प्रशिक्षण की आवश्यकता नहीं – चित्र समझने में सरल होते हैं। इसके लिए किसी विशेष ज्ञान व प्रशिक्षण की आवश्यकता नहीं होती। यही कारण है कि विज्ञापन में चित्रों की सहायता ली जाती है।
7. अधिक समय तक स्मरणीय – विशाल व जटिल समंकों को याद रखना कठिन होता है, जबकि चित्रों द्वारा प्रदर्शित किए गए निष्कर्ष अधिक समय तक याद रहते हैं।
8. अधिक जानकारी देना – चित्र समंकों को सापेक्ष रूप में प्रस्तुत करते हैं। साथ में वे समंकों में विद्यमान प्रवृत्ति और उस प्रवृत्ति में परिवर्तनों की भी स्पष्ट करते हैं।
प्रश्न 6.
चित्र रचना के सामान्य नियम क्या हैं? चित्रमय प्रदर्शन की सीमाएँ बताइए।
उत्तर :
चित्र रचना के सामान्य नियम
चित्रे रचना एक कला है। इसे अधिक प्रभावशाली बनाने के लिए कुछ सामान्य नियमों का पालन करना होता है। ये सामान्य नियम निम्नलिखित हैं—
- चित्र आकर्षक, स्वच्छ व प्रभावशाली होने चाहिए।
- ज्यामितीय आकृतियों की माप शुद्ध एवं अनुपात के हिसाब से होनी चाहिए अन्यथा निष्कर्ष भ्रामक होंगे।
- चित्र न तो बहुत बड़ा होना चाहिए और न बहुत छोटा।
- चित्र रेखापत्र के मध्य में होना चाहिए।
- कागज के आकार तथा समंकों की प्रकृति के आधार पर मापदण्ड का उल्लेख चित्र के एक कोने में होना चाहिए।
- प्रत्येक चित्र के ऊपर उचित परन्तु स्पष्ट व संक्षिप्त शीर्षक होना चाहिए। आवश्यकतानुसार उपशीर्षक भी दिए जाने चाहिए।
- पटरी, परकार व चाँदे की सहायता से चित्र शुद्ध बनाए जाने चाहिए। निर्धारित मापदण्ड का पूर्णत: पालन किया जाना चाहिए।
- चित्र के ऊपर कोने में उपयुक्त चिह्नों द्वारा विभिन्न तथ्यों के संकेत दिए जाने चाहिए।
- विभिन्न प्रकार के समंकों को चित्रित करने के लिए उपयुक्त विधि का चुनाव करना चाहिए।
- चित्र बनाने में साधन एवं शक्ति का दुरुपयोग नहीं किया जाना चाहिए।
- चित्रों को मोटी या दोहरी रेखाओं से घेर देना चाहिए।
- चित्र में आँकड़ों के महत्त्वपूर्ण अंशों को गहरे रंग से प्रदर्शित करना चाहिए।
चित्रमय प्रदर्शन की सीमाएँ
चित्र तथ्यों को केवल मोटे रूप में प्रस्तुत करते हैं; अतः चित्र उन व्यक्तियों के लिए भ्रामक होते हैं जो सावधानीपूर्वक अध्ययन किए बिना ही उनसे निष्कर्ष निकाल लेते हैं। एम० जे० मोरोने के शब्दों में-“किसी चित्र का अध्ययन करने के लिए पर्याप्त चौकन्ना रहना आवश्यक होता है। वह इतना सरल, इतना स्पष्ट तथा इतना मनभावी होती है कि असावधान व्यक्ति आसानी से मूर्ख बन जाता है।” चित्रमय प्रदर्शन की प्रमुख सीमाएँ निम्नलिखित हैं
- चित्रों की उपयोगिता सामान्य व्यक्ति के लिए है, किसी विशेषज्ञ के लिए नहीं।
- चित्रों के माध्यम से विभिन्न मूल्यों का सूक्ष्म अन्तर प्रदर्शित करना सम्भव नहीं होता।
- चित्र अनेक प्रकार की तुलना करने में अनुपयोगी होते हैं।
- जब मापों के मध्य विशाल अन्तर होता है तो उस अन्तर को चित्रों द्वारा प्रदर्शित करना कठिन हो जाता है।
- चित्रों को और अधिक निर्वचन करना सम्भव नहीं होता। 6. गलत मापदण्ड पर बने चित्र भ्रामक होते हैं।
- चित्र निष्कर्ष निकालने का केवल एक साधन है; अत: इसका प्रयोग सारणियों के साथ किया जाना चाहिए।
- सन्निकट मूल्यों पर आधारित होने के कारण चित्र तथ्यों का यथार्थ प्रदर्शन नहीं कर पाते।
- तुलनात्मक अध्ययन के लिए समंकों का सजातीय होना आवश्यक है।
प्रश्न 7.
समंकों के बिन्दुरेखीय प्रदर्शन का महत्त्व बताइए।
उत्तर :
आँकड़ों को स्पष्ट, आकर्षक एवं रुचिकर ढंग से प्रस्तुत करने के लिए सांख्यिकीय अनुसन्धान में बिन्दुरेखीय चित्रों का प्रदर्शन किया जाता है। इनका निर्माण बिन्दुरेखीय पत्र (ग्राफ पेपर) पर किया जाता है। ये चित्र दो चरों के परस्पर सम्बन्ध अथवा परस्पर निर्भरता को अधिक अच्छे ढंग से समझने में सहायक होते हैं। इनके माध्यम से दो चरों में होने वाले परिवर्तन का अनुमान अधिक शीघ्रता से लगाया जा सकता है।
बिन्दुरेखीय चित्रों का महत्त्व बिन्दुरेखीय चित्रों के महत्त्व को निम्नलिखित प्रकार से स्पष्ट किया जा सकता है
1. तुलना करने तथा सह – सम्बन्ध दिखाने में सहायक–बिन्दुरेखीय चित्र समंकों अथवा तथ्यों की तुलना करने में सहायक हैं इनसे केवले तुलना में ही सहायता नहीं मिलती अपितु दो चरों (Variables) में क्या सम्बन्ध है इसका भी पता चला जाता है।
2. सभी प्रकार के व्यक्तियों के लिए उपयोगी – बिन्दुरेखीय चित्र साधारण व्यक्तियों तथा सांख्यिकीय के छात्रों और अनुसन्धानकर्ता सभी प्रकार के व्यक्तियों के लिए उपयोगी हैं क्योंकि इनसे हमें तथ्यों का सरसरी ज्ञान मात्र ही नहीं होता अपितु चरों के पारस्परिक सम्बन्धों तथा परिवर्तन की दिशाओं का पता भी सरलता से हो जाता है।
3. आँकों के परिशुद्ध प्रदर्शन में सहायक – बिन्दुरेखीय चित्र अधिक स्पष्ट, सुबोध एवं परिशुद्ध होते हैं क्योंकि इनमें प्रत्येक बिन्दु तथा रेखा को अपना विशिष्ट महत्त्व होता है।
4. सांख्यिकीय अनुमापन में सहायक – बिन्दुरेखीय चित्रों से हमें भूयिष्ठक तथा मध्यका का भी अनुमान हो जाता है। छूटी हुई संख्या का पता लगाने अथवा किसी विशेषता की व्याख्या करने में बिन्दुरेखीय चित्र सहायक हैं।
5. आँकड़ों की विवेचना में सहायक – बिन्दुरेखीय चित्रों से समय-क्रम (Time series), सतत पदमालाओं (Continuous series) तथा आवृत्ति वितरण (Frequency distribution) का प्रदर्शन भी सम्भव हैं आन्तरगणन (Interpolation) का भी इन चित्रों से पता चल जाता है। इस . प्रकार ये आँकड़ों की विवेचना में भी सहायक हैं।
6. समय तथा धन की बचत – बिन्दुरेखीय चित्र अन्य चित्रों की अपेक्षा सरलता से बनाए जा सकते हैं, इसलिए समय तथा धन की बचत होती है। इनमें केवल ग्राफ पेपर, पेंसिल, रबर तथा पैमाने की ही आवश्यकता पड़ती है।
7. आकर्षक व प्रभावशाली – बिन्दुरेखीय चित्र बहुत ही आकर्षक होते हैं। उन्हें देखकर कोई भी व्यक्ति आसानी से प्रभावित हो जाता है।
8. समझने में सरल – समंकों की अव्यवस्थित एवं विशाल राशि बिन्दुरेख के द्वारा सरल व सुबोध बन जाती है जिसे साधारण व्यक्ति भी सरलता से समझ लेता है।
9. स्थायी प्रभाव – संख्या सम्बन्धी सूचनाओं को हम कुछ समय उपरान्त भूल जाते हैं किन्तु बिन्दुरेखाओं को प्रभाव पर्याप्त अंशों में स्थायी होता है।