UP Board Solutions for Class 11 Physics Chapter 3 Motion in a Straight Line ( सरल रेखा में गति)

These Solutions are part of UP Board Solutions for Class 11 Physics. Here we have given UP Board Solutions for Class 11 Physics Chapter 3 Motion in a Straight Line ( सरल रेखा में गति).

अभ्यास के अन्तर्गत दिए गए प्रश्नोत्तर

प्रश्न 1:
नीचे दिए गए गति के कौन-से उदाहरणों में वस्तु को लगभग बिन्दु वस्तु माना जा सकता है

(a) दो स्टेशनों के बीच बिना किसी झटके के चल रही कोई रेलगाड़ी।
(b) किसी वृत्तीय पथ पर साइकिल चला रहे किसी व्यक्ति के ऊपर बैठा कोई बन्दर।
(c) जमीन से टकराकर तेजी से मुड़ने वाली क्रिकेट की कोई फिरकती गेंद।
(d) किसी मेज के किनारे से फिसलकर गिरा कोई बीकर।
उत्तर:
(a) रेलगाड़ी दो स्टेशनों के बीच बिना झटके के चल रही है; अत: दोनों स्टेशनों के बीच की दूरी को रेलगाड़ी की लम्बाई की तुलना में अधिक माना जा सकता है। इसलिए रेलगाड़ी को बिन्दु वस्तु माना जाएगा।
(b) चूंकि बन्दर द्वारा यथोचित समय में तय की गई दूरी अधिक है; अत: बन्दर को बिन्दु वस्तु माना जाएगा।
(c) चूंकि गेंद का मुड़ना सरल नहीं है; अतः यथोचित समय में गेंद द्वारा तय की गई दूरी अधिक नहीं है। इसलिए गेंद को बिन्दु वस्तु नहीं माना जा सकत
(d) चूंकि बीकर मेज के किनारे से फिसलकर गिरता है; अतः यथोचित समय में इसके द्वारा तय की गई दूरी अधिक नहीं है। इसलिए इसे बिन्दु वस्तु नहीं माना जा सकता।

प्रश्न 2:
दो बच्चे A व B अपने विद्यालय से लौटकर अपने-अपने घर मे क्रमशः P तथा २ को जा रहे हैं। उनके स्थिति-समय (x-t) + ग्राफ चित्र-3.1 (a) में दिखाए गए हैं। नीचे लिखे कोष्ठकों में सही प्रविष्टियों को चुनिए

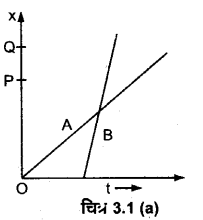
(a) B/A की तुलना में A/B विद्यालय से निकट रहता है।
(b) B/A की तुलना में A/B विद्यालय से पहले चलता है।
(c) B/A की तुलना में A/B तेज चलता है।
(d) A और B घर (एक ही/भिन्न) समय पर पहुँचते हैं।
(e) A/B सड़क पर B/A से (एक बार/दो बार) आगे हो जाते हैं।
उत्तर:
(a) B की तुलना में A विद्यालय से निकट रहता है, क्योंकि B अधिक दूरी तय करता है [OP< OQ]
(b) B की तुलना में A विद्यालय से पहले चलता है, क्योंकि A के लिए गति प्रारम्भ का समय t  = 0 है परन्तु B के गति प्रारम्भ के लिए समय हैं का निश्चित धनात्मक मान है।

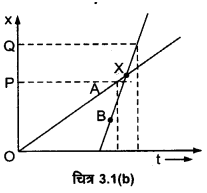
(c) A की तुलना में B तेज चलता है, क्योकि B के ग्राफ का ढाल A के ग्राफ के ढाल से अधिक है।
(d) A और B घर भिन्न समय पर पहुँचते हैं।
(e) B सड़क और A से एक बार आगे हो जाता है (प्रतिच्छेद बिन्दु X के बाद)।

प्रश्न 3:
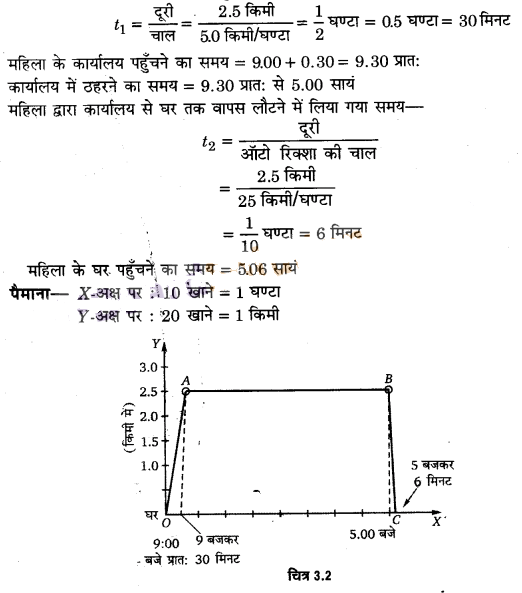
एक महिला अपने घर से प्रातः 9.00 बजे 2.5 km दूर अपने कार्यालय के लिए सीधी सड़क पर 5 kmh^-1 चाल से चलती है। वहाँ वह सायं 5.00 बजे तक रहती है और 25 kmh^-1 की चाल से चल रही किसी ऑटो रिक्शा द्वारा अपने घर लौट आती है। उपयुक्त पैमाना चुनिए तथा उसकी गति का x-t ग्राफ खींचिए।
हल:
महिला द्वारा घर से कार्यालय तक पहुँचने में लिया गया समय,

प्रश्न 4:
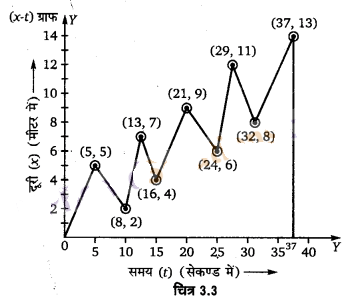
कोई शराबी किसी तंग गली में 5 कदम आगे बढ़ता है और 3 कदम पीछे आता है, उसके बाद फिर 5 कदम आगे बढ़ता है और 3 कदम पीछे आता है, और इसी तरह वह चलता रहता है। उसका हर कदम 1m लम्बा है और 1s समय लगता है। उसकी गति का x-t ग्राफ खींचिए। ग्राफ से तथा किसी अन्य विधि से यह ज्ञात कीजिए कि वह जहाँ से चलना प्रारम्भ करता है वहाँ से 13 m दूर किसी गड्ढे में कितने समय पश्चात गिरता है?
हल:
ग्राफ (चित्रे 3.3) से स्पष्ट है कि शराबी गति आरम्भ करने के स्थान से 13 किमी दूर गड्ढे में 37 सेकण्ड बाद गिरेगा। (∵13 मी के संगत ग्राफ से समय-अक्ष पर समय 37 सेकण्ड है।)

गणना:
प्रथम 8 कदम अर्थात् 8 सेकण्ड में शराबी का गत्यारम्भ के स्थान से विस्थापन अर्थात् उसके द्वारा तय नेट दूरी = (5 – 3) मी = 2 मी
इस प्रकार अगले 8 कदम तक (16 कदमों में) अर्थात्
16 सेकण्ड में नेट दूरी = (2+ 2) मी = 4 मी
24 कदमों में अर्थात् 24 सेकण्ड में नेट दूरी = (2+2+ 2) मी = 6 मी 32 कदमों में अर्थात् 32 सेकण्ड में नेट दूरी ।
= (2+2+ 2 + 2) मी = 8 मी
37 कदमों में अर्थात् 37 सेकण्ड में नेट दूरी = 8 मी + 5 मी = 13 मी
अतः गत्यारम्भ के स्थान से 13 मी दूर स्थित गड्ढे में गिरने में शराबी द्वारा लिया गया समय = 37 कदमों का समय = 37 सेकण्ड

प्रश्न 5:
कोई जेट वायुयान 500 kmh^-1 की चाल से चल रहा है और यह जेट वायुयान के सापेक्ष 1500 kmh^-1 की चाल से अपने दहन उत्पादों को बाहर निकालता है। जमीन पर खड़े किसी प्रेक्षक के सापेक्ष इन दहन उत्पादों की चाल क्या होगी?
हल:
जेट का वेग = ν_J = – 500 km h^-1 (प्रेक्षक से दूर)
जेट के सापेक्ष दहन उत्पाद बाहर निकालने का आपेक्षिक वेग = ν_eJ = 1500 km h^-1
यदि बाहर निकलने वाले उत्पादों का वेग ν_e हो तो ν_eJ = ν_e – ν_J
या
ν_e = ν_eJ +ν_J = 1500+ (- 500) = 1000 km/h

प्रश्न 6:
सीधे राजमार्ग पर कोई कार126 kmh-1 की चाल से चल रही है। इसे 200 m की दूरी पर रोक दिया जाता है। कार के मन्दन को एकसमान मानिए और इसका मान निकालिए। कार को रुकने में कितना समय लगा?
हल:
कार की प्रारम्भिक चाल, u = 126 किमी/घण्टा

प्रश्न 7:
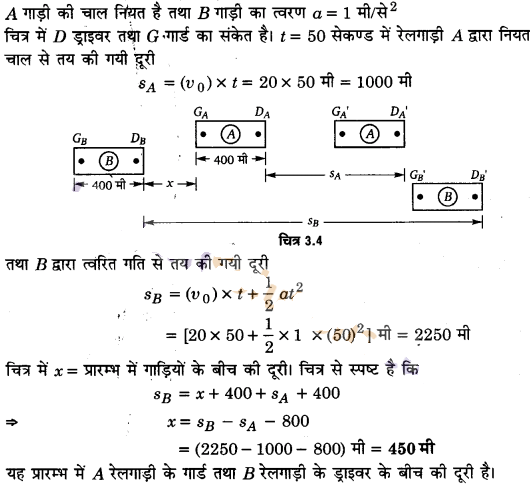
दो रेलगाड़ियाँ A व B दो समान्तर पटरियों पर 72 kmh^-1 की एकसमान चाल से एक ही दिशा में चल रही हैं। प्रत्येक गाड़ी 400 m लम्बी है और गाड़ी A गाड़ी B से आगे है। B का चालक A से आगे निकलना चाहता है तथा 1 ms^-2 से इसे त्वरित करता है। यदि 50s के बाद B को गार्ड A के चालक से आगे हो जाता है तो दोनों के बीच आरम्भिक दूरी कितनी थी?
हल:
रेलगाड़ियों की प्रारम्भिक तथा अन्तिम स्थितियाँ चित्र 3.4 में दिखायी गयी हैं।
प्रत्येक गाड़ी की प्रारम्भिक चाल (ν0) = 72 किमी/घण्टा = 20 मी/से

प्रश्न 8:
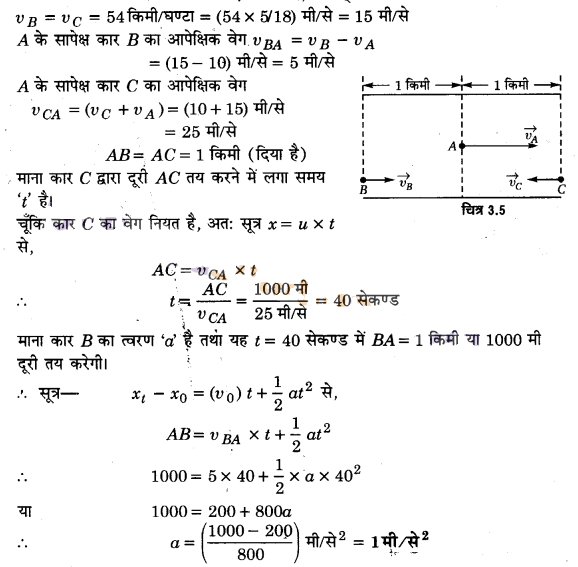
दो लेन वाली किसी सड़क पर कार A 36 kmh^-1 की चाल से चल रही है। एक-दूसरे की विपरीत दिशाओं में चलती दो कारें B वा  C जिनमें से प्रत्येक की चाल 54 kmh^-1 है, कार A तक पहुँचना चाहती है। किसी क्षण जब दूरी AB दूरी AC के बराबर है तथा दोनों 1 km हैं, कार B का चालक यह निर्णय करता है कि कार C के कार A तक पहुँचने के पहले ही वह कार A से आगे निकल जाए। किसी दुर्घटना से बचने के लिए कार B का कितना न्यूनतम त्वरण जरूरी है?
हल:
कार A की चाल = (36 x 5/18) मी/से = 10 मी/से
कार B तथा कार C दोनों की चाल एकसमान है, अर्थात्,

प्रश्न 9:
दो नगर A व B नियमित बस सेवा द्वारा एक-दूसरे से जुड़े हैं और प्रत्येक मिनट के बाद दोनों तरफ बसें चलती हैं। कोई व्यक्ति साइकिल से 20 kmh^-1 की चाल से A से B की तरफ जा रहा है और यह नोट करता है कि प्रत्येक 18 मिनट के बाद एक बस उसकी गति की दिशा में तथा प्रत्येक 6 मिनट बाद उसके विपरीत दिशा में गुजरती है। बस सेवाकाल T कितना है और बसें सड़क पर किस चाल (स्थिर मानिए) से चलती हैं?
हल:
माना ν_b = प्रत्येक बस की चाल
तथा ν_c = साइकिल-सवार की चाल
साइकिल सवार की गति की दिशा में चल रही बसों की आपेक्षिक चाल = ν_b – ν_c
साइकिल सवार की गति की दिशा में प्रत्येक 18 min या h बाद एक बस गुजरती है।

प्रश्न 10:
कोई खिलाड़ी एक गेंद को ऊपर की ओर आरम्भिक चाल 29 ms^-1 से फेंकता है,
(i) गेंद की ऊपर की ओर गति के दौरान त्वरण की दिशा क्या होगी?
(ii) इसकी गति के उच्चतम बिन्दु पर गेंद के वेग व त्वरण क्या होंगे?
(iii) गेंद के उच्चतम बिन्दु पर स्थान के समय को x= 0 व t = 0 चुनिए, ऊध्र्वाधर नीचे की ओर की दिशा को X-अक्ष की धनात्मक दिशा मानिए। गेंद की ऊपर की व नीचे की ओर
गति के दौरान स्थिति, वेग व त्वरण के चिह्न बताइए।
(iv) किस ऊँचाई तक गेंद ऊपर जाती है और कितनी देर के बाद गेंद खिलाड़ी के हाथों में आ . जाती है? [g = 9.8m s^-2 तथा वायु का प्रतिरोध नगण्य है।]
उत्तर:
(i) गेंद गुरुत्व के कारण त्वरण का प्रभाव अनुभव करती है जो सदैव ऊर्ध्वाधर नीचे की ओर कार्य करता है।
(ii) उच्चतम बिन्दु पर वेग = शून्य
उच्चतम बिन्दु पर त्वरण g = 9.8 m s^-2 (ऊध्र्वाधर नीचे की ओर)
(iii) ऊपर की ओर गति के लिए,
(a) स्थिति धनात्मक
(b) वेग ऋणात्मक
(c) त्वरण धनात्मक

नीचे की ओर गति के लिए,

(a) स्थिति धनात्मक
(b) वेग धनात्मक
(c) त्वरण धनात्मक

(iv) ऊपर की ओर गति के दौरान,

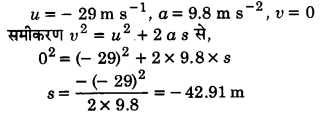
प्रश्न 11:
नीचे दिए गए कथनों को ध्यान से पढिए और कारण बताते हुए व उदाहरण देते हुए बताइए कि वे सत्य हैं या असत्य, एकविमीय गति में किसी कण की

(a) किसी क्षण चाल शून्य होने पर भी उसका त्वरण अशून्य हो सकता है।
(b) चाल शून्य होने पर भी उसका वेग अशून्य हो सकता है।
(c) चाल स्थिर हो तो त्वरण अवश्य ही शून्य होना चाहिए।
(d) चाल अवश्य ही बंढती रहेगी, यदि उसका त्वरण धनात्मक हो।
उत्तर:
(a) सत्य, सरल आवर्त गति करते कण की महत्तम विस्थापन की स्थिति में कण की चाल शून्य होती है, जबकि त्वरण महत्तम (अशून्य) होता है।
(b) असत्य, चाल शून्य होने का अर्थ है कि कण के वेग का परिमाण शून्य है।
(c) असत्य, एकसमाने वृत्तीय गति करते हुए कण की चाल स्थिर रहती है तो भी उसकी गति में। अभिकेन्द्र त्वरण कार्य करता है।
(d) असत्य, यह केवल जब सत्य हो सकता है जबकि चुनी गई धनात्मक दिशा गति की दिशा के अनुदिश हो।

प्रश्न 12:
किसी गेंद को 90 m की ऊँचाई से फर्श पर गिराया जाता है। फर्श के साथ प्रत्येक टक्कर में गेंद की चाल 1/10 कम हो जाती है। इसकी गति का t= 0 से 12s के बीच चाल-समय ग्राफ खींचिए।

उत्तर:

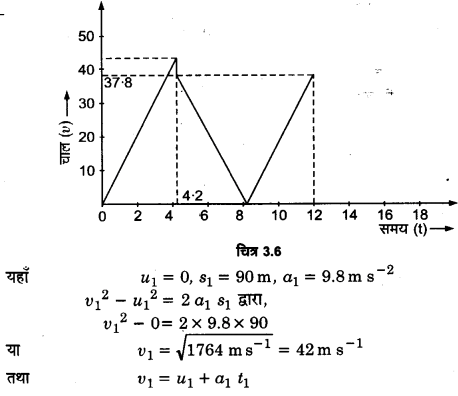
प्रश्न 13:
उदाहरण सहित निम्नलिखित के बीच के अन्तर को स्पष्ट कीजिए

(a) किसी समय अन्तराल में विस्थापन के परिमाण (जिसे कभी-कभी दूरी भी कहा जाता है)। और किसी कण द्वारा उसी अन्तराल के दौरान तय किए गए पथ की कुल लम्बाई।
(b) किसी समय अन्तराल में औसत वेग के परिमाण और उसी अन्तराल में औसत चाल
(किसी समय अंतराल में किसी कण की औसत चाल को समय अन्तराल द्वारा विभाजित की गई कुल पथ-लम्बाई के रूप में परिभाषित किया जाता है। प्रदर्शित कीजिए कि (a) व (b) दोनों में ही दूसरी राशि-पहली से अधिक या उसके बराबर है। समता का | चिह्न कब सत्य होता है? (सरलता के लिए केवल एकविमीय गति पर विचार कीजिए।)
उत्तर:
(a) विस्थापन के परिमाण का अर्थ है सीधी रेखा की कुल लम्बाई अर्थात् गति के प्रारम्भिक व अन्तिम बिन्दुओं के बीच की दूरी। कण द्वारा किसी समय अन्तराल में तय किए गए निश्चित पथ की कुल लम्बाई, उसी अन्तराल में गति के प्रारम्भिक व अन्तिम बिन्दुओं के बीच की दूरी भिन्न हो सकती है, जैसे चित्र-3.7 में A से B तक पहुँचने में पंथ
(1), दूरी अर्थात् पथ की लम्बाई को तथा पथ
(2) विस्थापन के परिमाण को प्रदर्शित करता है।


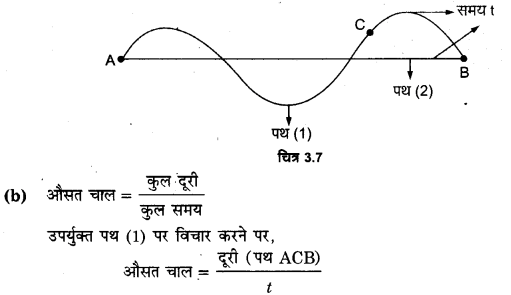
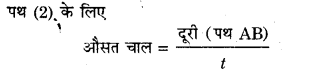
स्पष्ट है कि औसत चाल का मान औसत वेग के परिमाण से भिन्न है।
तथा औसत चाल का मान > औसत वेग को परिमाण
यदि A व B के बीच गति केवल पथ (2) पर हो तब औसत चाल =| औसत वेग ।
अतः स्पष्ट है कि प्रत्येक स्थिति में
| औसत चाल | ≥ | औसत वेगे ।

प्रश्न 14:
कोई व्यक्ति अपने घर से सीधी सड़क पर 5 kmh^-1 की चाल से 2.5 km दूर बाजार तक पैदल जाता है। परन्तु बाजार बन्द देखकर वह उसी क्षण वापस मुड़ जाता है तथा 7.5 km h ! की चाल से घर लौट आता है। समय अन्तराल (i) 0-30 मिनट, (ii) 0-50 मिनट, (iii) 0-40 मिनट की अवधि में उस व्यक्ति (a) के माध्य वेग का परिमाण तथा (b) की माध्य चाल क्या है? (नोट—आप इस उदाहरण से समझ सकेंगे कि औसत चाल को औसत-वेग के परिमाण के रूप में परिभाषित करने की अपेक्षा समय द्वारा विभाजित कुल पथ-लम्बाई के रूप में परिभाषित करना अधिक अच्छा क्यों है? आप थककर घर लौटे उस व्यक्ति को यह बताना नहीं चाहेंगे कि उसकी औसत चाल शून्य थी।)
हल:

प्रश्न 15:
हमने अभ्यास प्रश्न 13तथा 14में औसत चाल व औसत वेग के परिमाण के बीच के अन्तर को स्पष्ट किया है। यदि हम तात्क्षणिक चाल व वेग के परिमाण पर विचार करते हैं तो इस तरह का अन्तर करना आवश्यक नहीं होता। तात्क्षणिक चाल हमेशा तात्क्षणिक वेग के बराबर होती है। क्यों?
उत्तर:
जब हम यादृच्छिक समय अन्तरालों पर विचार करते हैं, विस्थापन का परिमाण सदैव दूरी के परिमाण के तुल्य होता है। अन्य शब्दों में,

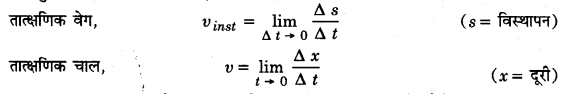
अत्यन्त लघु समय अन्तरालों (∆t → 0) में वस्तु की गंति की दिशा में कोई परिवर्तन नहीं माना जाता; अतः कुल पथ-लम्बाई (दूरी) तथा विस्थापन के परिमाण में कोई अन्तर नहीं होता। इस प्रकार तात्क्षणिक चाल सदैव तात्क्षणिक वेग के परिमाण के तुल्य होती है।

प्रश्न 16:
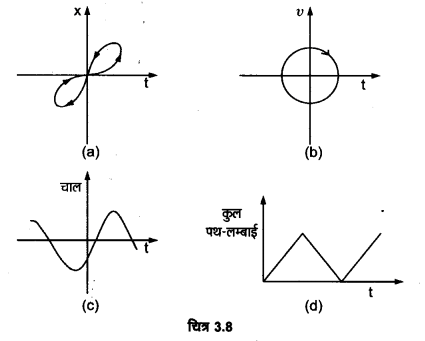
चित्र-8.8 में (a) से (d) तक के ग्राफों को ध्यान से देखिए और देखकर बताइए कि इनमें से कौन-सा ग्राफ एकविमीय गति को सम्भवतः नहीं दर्शा सकता?

उत्तर:
(a) यह ग्राफ एकविमीय गति प्रदर्शित नहीं करता, चूंकि किसी एक क्षण पर कण की दो स्थितियाँ एकविमीय गति में सम्भव नहीं होतीं।
(b) यह ग्राफ एकविमीय गति प्रदर्शित नहीं करता, चूँकि किसी क्षण पर कण का वेग धनात्मक तथा ऋणात्मक दोनों दिशाओं में है, जो एकविमीय गति में सम्भव नहीं है।
(c) यह ग्रफ भी एकविमीय गति प्रदर्शित नहीं करता, चूँकि यह ग्राफ कण की ऋणात्मक चाल व्यक्त कर रहा है तथा कण की चाल ऋणात्मक नहीं हो सकती।
(d) यह ग्राफ भी एकविमीय गति प्रदर्शित नहीं करता, चूँकि यह प्रदर्शित कर रहा है कि कुल पथ की लम्बाई एक निश्चित समय के पश्चात् घट रही है, परन्तु गतिमान कण की कुल पथ-लम्बाई कभी भी समय के साथ नहीं घटती।।

प्रश्न 17:
चित्र 3:9 में किसी कण की एकविमीय गति का ग्राफ दिखाया गया है। ग्राफ से क्या यह कहना ठीक होगा कि यह कण है t<0 के लिए किसी सरल रेखा में और है t > 0 के लिए किसी परवलीय पथ में गति करता है। यदि नहीं, तो ग्राफ के संगत किसी उचित भौतिक सन्दर्भ का सुझाव दीजिए।
उत्तर:
यह कहना ठीक नहीं होगा कि यह कण है t<0 के लिए किसी सरल रेखा में और t > 0 के लिए किसी परवलीय पथ में गति करता है, चूँकि x-t ग्राफ कण का पथ प्रदर्शित नहीं कर सकता।

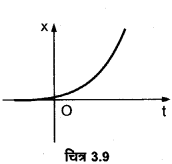
ग्राफ द्वारा t = 0 पर x= 0 प्रदर्शित है; अत: ग्राफ गुरुत्व के अन्तर्गत गिरती हुई किसी वस्तु की गति प्रदर्शित कर सकता है।

प्रश्न 18:
किसी राजमार्ग पर पुलिस की कोई गाड़ी 30 km/h की चाल से चल रही है और यह उसी दिशा में 192 km/h की चाल से जा रही किसी चोर की कार पर गोली चलाती है। यदि गोली की नाल मुखी चाल 150 ms^-1 है तो चोर की कार को गोली किस चाल के साथ आघात करेगी?
(नोट-उस चाल को ज्ञात कीजिए जो चोर की कार को हानि पहुँचाने में प्रासंगिक हो।)
हल:
चोर की कार की चाल ν_t = 192
किमी/घण्टा = (192 x 5/18)
मी/से = (160/3) मी/से

पुलिस की कार की चाल ν_p = 30
किमी/घण्टा = (30×5/18)
मी/से = (25/3) मी/से
पुलिस की कार (चाल) के सापेक्ष गोली की चाल, ν_bp = 150 मी/से
पुलिस की कार के सापेक्ष चोर की कार की आपेक्षिक चाल

चोर की कार से गोली के टकराने की चाल = पुलिस की कार के सापेक्ष गोली की आपेक्षिक चाल – पुलिस की कार के सापेक्ष चोर की कार की चाल = vbp – vtp
= 150 मी/से – 45 मी/से = 105 मी/से

प्रश्न 19:
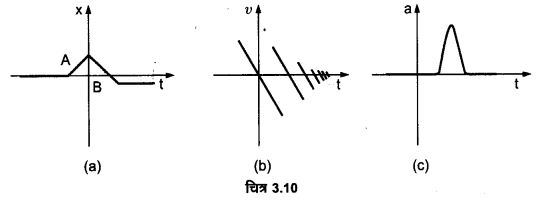
चित्र 3.10 में दिखाए गए प्रत्येक ग्राफ के लिए किसी उचित भौतिक स्थिति का सुझाव दीजिए

उत्तर:
(a) x-t ग्राफ प्रदर्शित कर रहा है कि प्रारम्भ में x शून्य है, फिर यह एक स्थिर मान प्राप्त करता है, पुनः यह शून्य हो जाता है तथा फिर यह विपरीत दिशा में बढ़कर अन्त में एक स्थिर मान (विरामावस्था) प्राप्त कर लेता है। अतः यह ग्राफ इस प्रकार की भौतिक स्थिति व्यक्त कर सकता है जैसे एक गेंद को विरामावस्था से फेंका जाता है और वह दीवार से टकराकर लौटती है तथा कम चाल से उछलती है तथा यह क्रम इसके विराम में पहुँचने तक चलता रहता है।
(b) यह ग्राफ प्रदर्शित कर रहा है कि वेग समय के प्रत्येक अन्तराल के साथ परिवर्तित हो रहा है तथा प्रत्येक बार इसका वेग कम हो रहा है। इसलिए यह ग्राफ एक ऐसी भौतिक स्थिति को व्यक्त कर सकता है जिसमें एक स्वतन्त्रतापूर्वक गिरती हुई गेंद (फेंके जाने पर) धरती से टकराकर कम चाल से पुनः उछलती है तथा प्रत्येक बार धरती से टकराने पर इसकी चाल कम होती जाती है।
(c) यह ग्राफ प्रदर्शित करता है कि वस्तु अल्प समय में ही त्वरित हो जाती है। अत: यह ग्राफ एक ऐसी भौतिक स्थिति को व्यक्त कर सकता है जिसमें एकसमान चाल से चलती हुई गेंद को अत्यल्प समयान्तराल में बल्ले द्वारा टकराया जाता है।

प्रश्न 20:
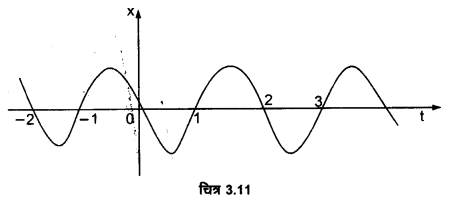
चित्र 3.11 में किसी कण की एकविमीय सरल आवर्ती गति के लिए x-t ग्राफ दिखाया गया है। (इस गति के बारे में आप अध्याय 14 में पढ़ेंगे) समय t = 0.3 s, 1.2 s, – 1.2s पर कण के स्थिति, वेग व त्वरण के चिह्न क्या होंगे?

हल:
सरल आवर्ती गति में, त्वरण, α= -ω²x जहाँ ω नियतांक (कोणीय आवृत्ति) है।
समय t = 0.3s पर, x ऋणात्मक है, x-t ग्राफ का ढाल ऋणात्मक है; अतः स्थिति एवं वेग ऋणात्मक हैं। चूंकि α = -ω²x);
अत: त्वरण धनात्मक है। समय t = 1.2 s पर, x धनात्मक है, x-t ग्राफ का ढाल भी धनात्मक है; अतः स्थिति एवं वेग धनात्मक हैं। चूंकि α = ω²x; अतः त्वरण ऋणात्मक है।
समय t = -1.2s पर, x ऋणात्मक है, x-t ग्राफ का ढाल भी धनात्मक है; अतः वेग धनात्मक है। अन्त में त्वरण ‘α’ भी धनात्मक है।

प्रश्न 21:
चित्र 3.12 में किसी कण की एकविमीय गति का है ग्राफ दर्शाता है। इसमें तीन समान अन्तराल दिखाए गए हैं। किस अन्तराल में औसत चाल अधिकतम है और किसमें न्यूनतम है? प्रत्येक अन्तराल के लिए औसत वेग का चिह्न बताइए।
उत्तर:

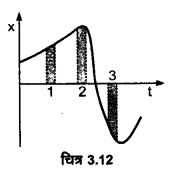
हम जानते हैं कि लघु अन्तरालों में x-t ग्राफ का ढाल उस अन्तराल में कण की औसत चाल व्यक्त करता है। ग्राफ से यह स्पष्ट है कि अन्तराल (3) में ग्राफ का ढाल अधिकतम है, परन्तु अन्तराल (2) में न्यूनतम है। अतः औसत चाल अन्तराल (3) में अधिकतम तथा अन्तराल (2) में न्यूनतम होगी। इसके अतिरिक्त अन्तराल (1) तथा (2) में ढाल धनात्मक है परन्तु अन्तराल (3) में ऋणात्मक; अत: अन्तराल (1) व (2) में औसत वेग धनात्मक है परन्तु अन्तराल (3) में ऋणात्मक।

प्रश्न 22:
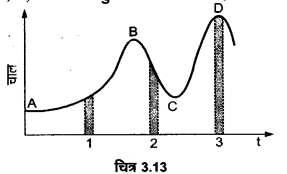
चित्र-3.13 में किसी नियत (स्थिर) दिशा के अनुदिश चल रहे कण.का चाल-समय ग्राफ दिखाया गया है। इसमें तीन समान समय अन्तराल दिखाए गए हैं। किस अन्तराल में औसत त्वरण का परिमाण अधिकतम होगा? किस अन्तराल में औसत चाल अधिकतम होगी? धनात्मक दिशा को गति की स्थिर दिशा चुनते हुए तीनों अन्तरालों में ν तथा a के चिह्न बताइए। A, B, C व D बिन्दुओं पर त्वरण क्या होंगे?

उत्तर:
(i) हम जानते हैं कि लघु अन्तरालों में ν-t ग्राफ के ढाल का परिमाण कण के औसत त्वरण को परिमाण देता है। दिए गए चित्र से स्पष्ट है कि ढाल का परिमाण
(2) में अधिकतम तथा
(3) में न्यूनतम है।
अत: औसत त्वरण का परिमाण अन्तराल (2) में अधिकतम तथा (3) में न्यूनतम होगा।
(ii) चित्र से स्पष्ट है कि औसत चाल अन्तराल (3) में अधिकतम तथा अन्तराल (1) में न्यूनतम है।
(iii) सभी तीनों अन्तरालों में चाल ν धनात्मक है। पुनः अन्तराल (1) में (ν-t) ग्राफ का ढाल धनात्मक है, जबकि अन्तराल (2) में ढाल (त्वरण a) ऋणात्मक है। चूंकि अन्तराल (3) में, ν-t ग्राफ समय-अक्ष के समान्तर है; अत: इस अन्तराल में a शून्य है।
(iv) A, B, C तथा D.बिन्दुओं पर, ν-t ग्राफ समय-अक्ष के समान्तर है। इसलिए सभी चारों बिन्दुओं पर ‘a’ शून्य है।

अतिरिक्त अभ्यास

प्रश्न 23:
कोई तीन पहिये वाला स्कूटर अपनी विरामावस्था से गति प्रारम्भ करता है। फिर 10 s तक किसी सीधी सड़क पर 1m s^-2 के एकसमान त्वरण से चलता है। इसके बाद वह एकसमान वेग से चलता है। स्कूटर द्वारा नावें सेकण्ड (n= 1, 2, 3, ……) में तय की गई दूरी को n के सापेक्ष आलेखित कीजिए। आप क्या आशा करते हैं कि त्वरित गति के दौरान यह ग्राफ कोई सरल रेखा या कोई परवलय होगा?
हल:
हम जानते हैं कि


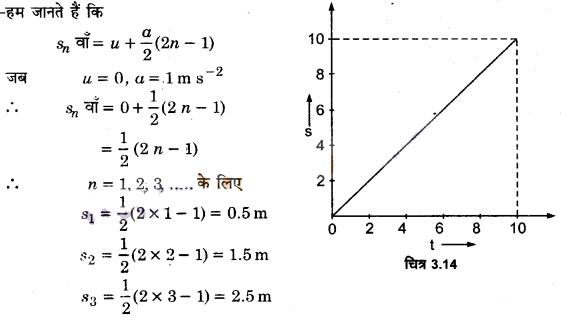
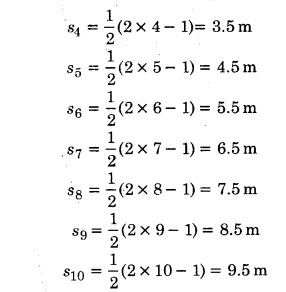
चित्र-3.14 में प्रदर्शित ग्राफ से स्पष्ट है कि त्वरित गति के दौरान हमें एक सरल रेखा प्राप्त होती है।

प्रश्न 24:
किसी स्थिर लिफ्ट में (जो ऊपर से खुली है) कोई बालक खड़ा है। वह अपने पूरे जोर से एक गेंद ऊपर की ओर फेंकता है जिसकी प्रारम्भिक चाल 49 ms^-1 है। उसके हाथों में गेंद के वापस आने में कितना समय लगेगा? यदि लिफ्ट ऊपर की ओर 5 m s^-1 की एकसमान चाल से गति करना प्रारम्भ कर दे और वह बालक फिर गेंद को अपने पूरे जोर से फेंकता तो कितनी देर में गेंद उसके हाथों में लौट आएगी?
हल:

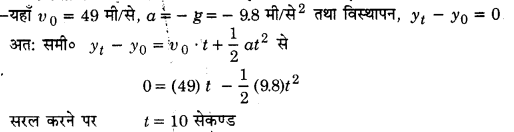
जब लिफ्ट ऊपर की ओर 5 मी/से की चाल से गति आरम्भ करे तो भी गेंद अब भी पूर्व की भाँति 10 सेकण्ड ही लेगी, चूंकि गेंद की बालक के सापेक्ष आपेक्षिक गति जब भी 49 मी/से ही होगी।

प्रश्न 25:
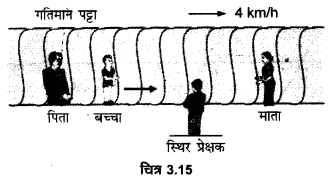
क्षैतिज में गतिमान कोई लम्बा पट्टा (चित्र-3.15) 4 km/h की चाल से चल रहा है। एक बालक इस पर (पट्टे के सापेक्ष) 9 km/h की चाल से कभी आगे, कभी पीछे अपने माता-पिता के बीच दौड़ रहा है। माता व पिता के बीच 50 m की दूरी है। बाहर किसी स्थिर प्लेटफार्म पर खड़े एक प्रेक्षक के लिए, निम्नलिखित का मान प्राप्त करिए
(a) पट्टे की गति की दिशा में दौड़ रहे बालक की चाल,
(b) पट्टे की गति की दिशा के विपरीत दौड़ रहे बालक की चाल,
(c) बच्चे द्वारा (a) व (b) में लिया गया समय यदि बालक की गति का प्रेक्षण उसके माता या पिता करें तो कौन-सा उत्तर बदल जाएगा?

हल:

प्रश्न 26:
किसी 200 m ऊँची खड़ी चट्टान के किनारे से दो पत्थरों को एक साथ ऊपर की ओर 15 m s-1 तथा 30 m s-1 की प्रारम्भिक चाल से फेंका जाता है। इसका सत्यापन कीजिए कि संलग्न ग्राफ (चित्र-3.16) पहले पत्थर के सापेक्ष दूसरे पत्थर की आपेक्षिक स्थिति का समय के साथ परिवर्तन को प्रदर्शित करता है। वायु के प्रतिरोध को नगण्य मानिए और यह मानिए कि जमीन से टकराने के बाद पत्थर ऊपर की ओर उछलते नहीं। मान लीजिए g = 10 m s-2 ग्राफ के रेखीय व वक्रीय भागों के लिए समीकरण लिखिए।
हल:
पहले पत्थर के लिए,

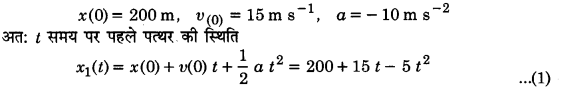
प्रश्न 27:
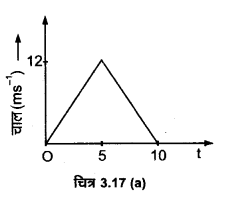
किसी निश्चित दिशा के अनुदिश चल रहे किसी कण का चाल-समय ग्राफ चित्र-3.17 में दिखाया गया है। कण द्वारा
(a) t = 0s से t= 10 s,
(b) t = 2s से 6s के बीच तय की गई दूरी ज्ञात कीजिए।
(a) तथा (b) में दिए गए अन्तरालों की अवधि मेंकण की औसत चाल क्या है?

हल:
(a) t = 0 से t = 10 सेकण्ड के बीच कण द्वारा तय की गयी दूरी = ∆OAB का क्षेत्रफल

प्रश्न 28:
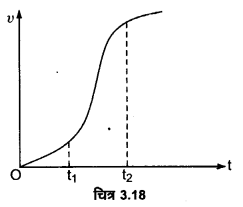
एकविमीय गति में किसीकण का वेग-समय ग्राफ चित्र-3.18 में दिखाया गया है-नीचे दिए सूत्रों में t₁ से t₂ तक के समय अन्तराल की अवधि में कण की गति का वर्णन करने के लिए कौन-से सूत्र सही हैं


उत्तर:
(i) यह सही नहीं है, क्योंकि t₁ , तथा t₂, के बीच अन्तराल में d स्थिर नहीं है।
(ii) यह सूत्र भी सही नहीं है। यहाँ भी a स्थिर नहीं है।
(iii) यह सूत्र सही है।
(iv) यह सूत्र सही है।
(v) यह सूत्र सही नहीं है, क्योंकि इसमें औसत त्वरण को प्रयुक्त नहीं किया जा सकता।
(vi) यह सूत्र सही है।

परीक्षोपयोगी प्रश्नोत्तर

बहुविकल्पीय प्रश्न

प्रश्न 1:
यदि कोई वस्तु पृथ्वी की ओर मुक्त रूप से गिरती है, तो वस्तु की गति होगी
(i) एकविमीय
(ii) द्विविमीय गति
(iii) त्रिविमीय गुति
(iv) इनमें से कोई नहीं
उत्तर:
(i) एकविमीय

प्रश्न 2:
एक वस्तु द्वारा चली गई दूरी समय के अनुक्रमानुपाती है। इसका अर्थ है कि वस्तु
(i) समान चाल से चल रही है ।
(ii) की चाल शून्य है।
(iii) समान वेग से चल रही है।
(iv) समान त्वरण से चल रही है।
उत्तर:
(iii) समान वेग से चल रही है।

प्रश्न 3:
एक वस्तु का चाल-समय ग्राफ X-अक्ष के समानान्तर एक रेखा है। इसका अर्थ है।
(i) वस्तु समान गति से चल रही है।
(ii) वस्तु असमान गति से चल रही है।
(iii) वस्तु स्थिर है।
(iv) वस्तु त्वरित गति से चल रही है।
उत्तर:
(i) वस्तु समान गति से चल रही है।

प्रश्न 4:
वेग अथवा चाल का मात्रक है।
(i) मीटर-सेकण्ड
(ii) मीटर/सेकण्ड
(iii) मीटर/सेकण्ड²
(iv) मीटर-सेकण्ड²
उत्तर:
(ii) मीटर/सेकण्ड

प्रश्न 5:
दो रेलगाड़ियाँ क्रमश u तथा v वेग से विपरीत दिशाओं में चल रही हैं। पहली गाड़ी के सापेक्ष दूसरी गाड़ी का वेग होगा
(i) v- u
(ii) v + u
(iii) u – v
(iv) शून्य
उत्तर:
(ii) u +v

प्रश्न 6:
पृथ्वी तल से ऊध्र्वाधर ऊपर की ओर फेंका गया पिण्ड जब महत्तम ऊँचाई पर होता है, तो उसका
(i) वेग अधिकतम होता है।
(ii) त्वरण शून्य होता है।
(iii) त्वरण अधिकतम होता है।
(iv) वेग शून्य होता है।
उत्तर:
(iv) वेग शून्य होता है

प्रश्न 7:
एक वस्तु विरामावस्था से hऊँची मीनार की चोटी से गिरती है। पृथ्वी पर पहुँचने पर उसका वेग होगा

उत्तर:
(iii)

प्रश्न 8:
दो पत्थर परस्पर 3:5 के अनुपात के वेगों से ऊध्र्वाधरतः ऊपर की ओर फेंके जाते हैं। यदि वे क्रमश  h₁ व h₂ ऊँचाई तक जाएँ तो h₁: h₂ बराबर होगा
(i) 3: 5
(ii) 5 : 3
(iii) 15 : 1
(iv) 9: 25
उत्तर:
(iv) 9:25

प्रश्न 9:
एक कण का प्रारम्भिक वेग 10 मीटर/सेकण्ड² तथा मन्दन 2 मीटर/सेकण्ड है। कण द्वारा 5वें सेकण्ड में चली गई दूरी है।
(i) 1 मीटर
(ii) 19 मीटर
(iii) 5 मीटर
(iv) 75 मीटर
उत्तर:
(i) 1 मीटर

प्रश्न 10:
मीनार की चोटी से छोड़ा गया पत्थर पृथ्वी पर 4 सेकण्ड में पहुँचता है। मीनार की ऊँचाई है
(i) 20 मीटर
(ii) 40 मीटर
(iii) 80 मीटर
(iv) 160 मीटर
उत्तर:
(iii) 80 मीटर

प्रश्न 11:
एक पिण्ड को पृथ्वी से ऊपर की ओर 100 मी/सेकण्ड के वेग से फेंका जाता है। वह वापस पृथ्वी पर पहुँचने में समय लेगा (लगभग)
(i) 10 सेकण्ड
(ii) 20 सेकण्ड
(iii) 15 सेकण्ड
(iv) 5 सेकण्ड
उत्तर:
(ii) 20 सेकण्डे

प्रश्न 12:
एक पिण्ड X-अक्ष की दिशा में इस प्रकार चलता है कि निर्देशांक x, समय t (सेकण्ड) के साथ समीकरण = 2- 5t + 6t² मीटर के अनुसार परिवर्तित होता है। पिण्ड का प्रारम्भिक वेग है।
(i) – 5 मी/से
(ii)-3 मी/से
(iii) 6 मी/से
(iv) 3 मी/से
उत्तर:
(i) -5 मी/से।

प्रश्न 13:
1000 किग्रा द्रव्यमान की एक कार 40 मी/से की चाल से गति कर रही है। इसे रोकने के लिए ब्रेक लगाया जाता है। यदि ब्रेक का बल 4000 न्यूटन हो, तो कार को रोकने में आवश्यक समय होगा।
(i) 5 सेकण्ड
(ii) 10 सेकण्ड
(iii) 15 सेकण्ड
(iv) 20 सेकण्ड
उत्तर:
(ii) 10 सेकण्ड

प्रश्न 14:
2000 किग्रा द्रव्यमान की एक कार 20 मी/से की चाल से गति कर रही है। ब्रेक का प्रयोग कर कार को रोका जाता है। यदि मन्दक बल 2000 N हो, तो कार को रोकने में आवश्यक समय होगा।
(i) 5 सेकण्ड़
(ii) 10 सेकण्ड
(iii) 15 सेकण्ड
(iv) 20 सेकण्ड
उत्तर:
(iv) 20 सेकण्ड

प्रश्न 15:
एक कार सर्वप्रथम 5 किमी दूरी पूर्व दिशा में तय करती है उसके बाद 12 किमी दूरी उत्तर दिशा में तय करती है। कार द्वारा तय की गई कुल दूरी तथा विस्थापन होगा
(i) 17 किमी, 13 किमी.
(ii) 15 किमी, 40 किमी
(iii) 50 किमी, 35 किमी
(iv) 5 किमी, 35 किमी
उत्तर:
(i) 17 किमी, 13 किमी

प्रश्न 16:
M.K.S. पद्धति में त्वरण का मात्रक है।
(i) मीटर/सेकण्ड
(ii) न्यूटन/मीटर
(iii) मीटर/सेकण्ड²
(iv) किग्रा-मीटर/सेकण्ड
उत्तर:
(iii) मीटर/सेकण्ड²

प्रश्न 17:
चाल-समय ग्राफ का ढाल प्रदर्शित करता है।
(i) चाल
(ii) त्वरण
(iii) विस्थापन
(iv) द्वेग
उत्तर:
(ii) त्वरण

प्रश्न 18:
एक गतिमान वस्तु द्वारा तय की गयी दूरी समय के वर्ग के अनुक्रमानुपाती है। वस्तु का त्वरण
(i) बढ़ रहा है।
(ii) घट रहा है।
(iii) शून्य है
(iv) नियत है।
उत्तर:
(iv) नियत है।

प्रश्न 19:
जड़त्वीय निर्देश तन्त्र में त्वरण a का मान शून्य होता है, जब
(i) F > 1
(ii) F<1
(iii) F =1
(iv) F = 0
उत्तर:
(iv) F= 0

अतिलघु उत्तरीय प्रश्न

प्रश्न 1:
विस्थापन से क्या तात्पर्य है?
उत्तर:
किसी गतिशील वस्तु की प्रारभिक और अन्तिम स्थितियों के बीच न्यूनतम दूरी को विस्थापन कहते हैं। यह एक सदिश राशि है।

प्रश्न 2:
दूरी तथा विस्थापन में से कौन सदिश राशि है?
उत्तर:
विस्थापन।

प्रश्न 3:
वेग-समय ग्राफ तथा समय-अक्ष के बीच का क्षेत्रफल क्या प्रदर्शित करता है?
उत्तर:
विस्थापन।

प्रश्न 4:
क्या किसी वस्तु का वेग नियत तथा चाल परिवर्ती हो सकती है?
उत्तर:
नहीं।

प्रश्न 5:
स्थिति-समय ग्राफ का ढाल क्या प्रदर्शित करता है?
उत्तर:
वेग।

प्रश्न 6:
एक वस्तु ऊध्वधर ऊपर की ओर फेंकी जाती है तथा वह h ऊँचाई तक जाकर प्रेक्षण बिन्दु पर लौट आती है। वस्तु द्वारा तय की गई दूरी व विस्थापन के मान बताइए।
उत्तर:
दूरी = 2h, विस्थापन = 0.

प्रश्न 7:
एक मीनार की चोटी से एक गेंद किसी निश्चित वेग से ऊध्वधर ऊपर की ओर तथा दूसरी गेंद उसी वेग से ठीक नीचे की ओर प्रक्षेपित की जाती हैं, कौन-सी गेंद को पृथ्वी से टकराने पर
वेग अधिक होगा?
उत्तर:
दोनों समान वेग से टकरायेंगी।

प्रश्न 8:
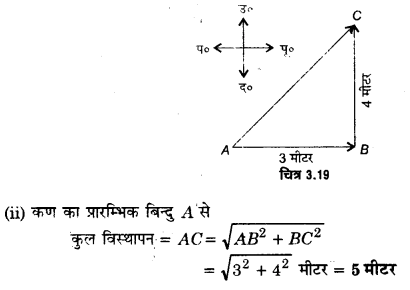
एक कण प्रारम्भ में 3 मीटर पूर्व एवं फिर 4 मीटर उत्तर की दिशा में चलकर अपनी यात्रा पूर्ण करता है। गणना कीजिए
(i) कण द्वारा चली गयी दूरी,
(ii) कण का विस्थापन।
हल:
(i) चित्र 3.19 से स्पष्ट है कि कण द्वारा चली गयी।
सम्पूर्ण दूरी = AB+ BC = 3+ 4 मीटर = 7 मीटर

प्रश्न 9:
अजड़त्वीय निर्देश तन्त्र क्या है?
उत्तर:
वे निर्देश तन्त्र, जिसमें न्यूटन के गति विषयक नियमों का पालन नहीं होता है, अजड़त्वीय निर्देश तन्त्र कहलाते हैं।

प्रश्न 10:
एक कार किसी दूरी के आधे भाग को 40 किमी/घण्टा तथा शेष बचे हुए भाग को 60 किमी/घण्टा की चाल से तय करती है। कार की औसत चाल की गणना कीजिए।
हल:
माना कुल दूरी x है तथा आधी-आधी दूरियों के समय क्रमशः t₁ एवं t₂ हैं।

प्रश्न 11:
ऊर्ध्वाधर दिशा में दागी गई एक गोली पुनः उसी बिन्दु पर आ गिरती है। उसके द्वारा तय की गई दूरी कितनी होगी?
उत्तर:
गोली पहले ऊपर की ओर जाकर फिर वापस नीचे की ओर उसी बिन्दु पर आकर गिरती है जिस बिन्दु से गोली छोड़ी गई थी। अत: गोली द्वारा चली गई दूरी उसके द्वारा तय की गई ऊंचाई की दोगुनी होगी।

प्रश्न 12:
तात्क्षणिक वेग क्या है?
उत्तर:
किसी क्षण विशेष पर गतिशील पिण्ड का जो चेग होता है, उसे तत्क्षणिक वेग कहते हैं। इसे dt द्वारा प्रदर्शित करते हैं।

प्रश्न 13:
विस्थापन-समय ग्राफ समय-अक्ष के समान्तर सरल रेखा है। वेग तथा त्वरण के मान क्या होंगे?
उत्तर:
दोनों शून्य।

प्रश्न 14:
वेग-समय ग्राफ का ढाल क्या प्रदर्शित करता है?
उत्तर:
चरण।

प्रश्न 15:
यदि त्वरण का S.I. मात्रक मी से 2 है, तो मन्दन का S.I. मात्रक क्या होगा?
उत्तर:
मी से^-2 ।

प्रश्न 16:
ऋणात्मक त्वरण से क्या तात्पर्य है?
उत्तर:
वेग घटने की समय दर ऋणात्मक त्वरण कहलाती है।

प्रश्न 17:
बताइए पृथ्वी पर वर्षा की बूंदें एकसमान वेग से गिरती हैं या एकसमान त्वरण से।
उत्तर:
एकसमान त्वरण से।

प्रश्न 18:
वेग-परिवर्तन की समय दर को क्या कहते हैं?
उत्तर:
त्वरण।

प्रश्न 19:
त्वरण-समय ग्राफ तथा समय-अक्ष के बीच का क्षेत्रफल क्या प्रदर्शित करता है?
उत्तर:
वेग-परिवर्तन।

प्रश्न 20:
एक बच्चा एकसमान वेग से चलती हुई ट्रेन, जो सीधी पटरियों पर गतिमान है, में बैठा है, वह एक गेंद हवा में उछालता है, थोड़े समय बाद गेंद कहाँ गिरेगी?
उत्तर:
उसके हाथ में।

प्रश्न 21:
एक मीनार की चोटी से एक गेंद क्षैतिज दिशा में किसी निश्चित वेग से फेंकी जाती है, उसी क्षण दूसरी गेंद वहीं से ऊर्ध्वाधर नीचे की ओर मुक्त रूप से गिरने के लिए छोड़ी जाती है,कौन-सी गेंद पृथ्वी पर पहले टकराएगी?
उत्तर:
दोनों गेंदें साथ-साथ टकरायेंगी, क्योंकि ऊध्र्वाधर दिशा में दोनों गेंदों के प्रारम्भिक वेग शून्य हैं, तथा दोनों पर त्वरण का मान g है।

प्रश्न 22:
एकसमान त्वरित गति करने वाले एक पिण्ड द्वारा 7वें तथा 9वें. सेकण्ड में तय की गई दूरियाँ क्रमशः 20 मी तथा 24मी हैं, तो वह पिण्ड 15वें सेकण्ड में कितनी दूरी तय करेगा?
हल:
7वें सेकण्ड में चली गयी दूरी = 20 मी

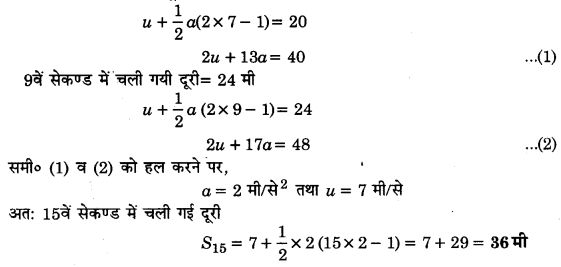
प्रश्न 23:
क्या कोई वस्तु जिसका वेग शून्य हो, त्वरित हो सकती है?
उत्तर:
हाँ, जब ई वस्तु अपनी गति की दिशा को उत्क्रमित (Reversal) करती है, तो क्षण भर के लिए उसका वेग शून्य हो जाता है, अपितु उस पर अब भी -a परिमाण को त्वरण कार्य करता है।

प्रश्न 24:
एक चलती हुई मोटरगाड़ी को ब्रेक लगाकर कुछ दूरी पर रोक लिया जाता है इसके लिए गति का समीकरण लिखिए।
उत्तर:
u² = 2ax, जहाँ a= त्वरण (मन्दन), x = दूरी तथा u = प्रारम्भिक वेग।

प्रश्न 25:
आपेक्षिक वेग से क्या तात्पर्य है?
उत्तर:
जब दो वस्तुएँ किसी वेग से गतिमान होती हैं तो प्रति सेकण्ड उनके बीच के विस्थापन में होने वाले परिवर्तन को आपेक्षिक वेग कहते हैं।

लघु उत्तरीय प्रश्न

प्रश्न 1:
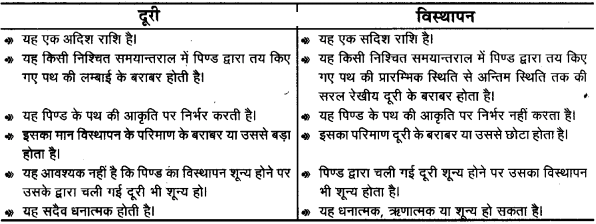
दूरी तथा विस्थापन में अंन्तर लिखिए।
उत्तर:
दूरी तथा विस्थापन में अन्तर

प्रश्न 2:
चाल तथा वेग में अन्तर लिखिए।
उत्तर:
चाल-किसी गतिशील वस्तु की चाल यह दर्शाती है कि वह वस्तु उस क्षण कितनी तेज चल रही है। किसी वस्तु द्वारा एकांक समय में चली गई दूरी को वस्तु की चाल कहते हैं।

यह एक अदिश राशि है।
वेग:
कोई वस्तु एकांक समयान्तराल में किसी दिशा में जितनी विस्थापित होती है, उसे उस दिशा में वस्तु का वेग कहते हैं। वेग एक सदिश राशि है।

प्रश्न 3:
परिवर्ती चाल तथा औसत चाल से क्या तात्पर्य है?
उत्तर:
परिवर्ती चाल-यदि कोई वस्तु समान समयान्तरालों में भिन्न-भिन्न दूरियाँ तय करती है तो वस्तु की चाल असमान या परिवर्ती कहलाती है। औसत चाल-अधिकतरे गतिशील वस्तुओं की चाल परिवर्तित होती रहती है तथा यह कई बार अपनी गति की दिशा भी बदलती है ऐसी अवस्था में उसकी औसत चाल ज्ञात की जाती है। अर्थात् किसी गतिमान वस्तु द्वारा तय की गई कुल दूरी तथा लिए गये कुल समय के अनुपात को औसत चाल कहते हैं।

प्रश्न 4:
क्या एक गतिशील वस्तु के लिए यह सम्भव है कि उसकी कुछ औसत चाल हो लेकिन औसत वेग शुन्य हो?
उत्तर:
हाँ, यह सम्भव है। उदाहरण-यदि कोई व्यक्ति किसी वृत्ताकार ट्रैक पर किसी स्थान से चलकर कुछ निश्चित समय पश्चात् उसी ट्रैक के उसी स्थान पर वापस लौट आता है, तो उसके द्वारा चली गयी दूरी = ट्रैक की परिधि तथा उसका विस्थापन = शून्य।
अत: उसकी औसत चाल = दूरी/समय ।
तथा औसत वेग = विस्थापन/समयं = 0 /समय = 0

प्रश्न 5:
10 ग्राम तथा 100 ग्राम वाली भिन्न द्रव्यमान की दो वस्तुएँ एकसमान ऊँचाई से गिराई जाती हैं। क्या वे एक समय पर पृथ्वी पर पहुँचेंगी? अपना उत्तर व्याख्या सहित लिखिए।
उत्तर:
दोनों वस्तुओं को प्रारम्भिक वेग 40 = शून्य तथा दोनों के द्वारा पृथ्वी तक पहुँचने में तय की गयी दूरी के भी समान है।

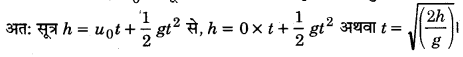
इस सूत्र में द्रव्यमान नहीं आ रहा है। अत: g नियत होने के कारण दोनों के लिए है समान होगा। यदि वायु का प्रतिरोध नगण्य मान लिया जाये जो द्रव्यमान पर निर्भर करता है, अतः दोनों वस्तुएँ एक समय पर पृथ्वी पर पहुँचेगी।

प्रश्न 6:
एक कण को 20 मी/से के प्रारम्भिक वेग से ऊपर की ओर फेंका जाता है। 3.0 सेकण्ड बाद कण द्वारा तय की गयी दूरी तथा विस्थापन की गणना कीजिए। (g= 10 मी/से²)।
हल:
दिया है, u = 20 मी/से, t= 3 सेकण्ड

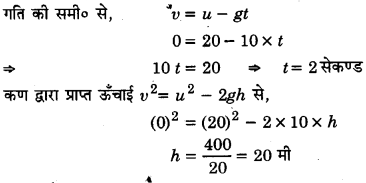
प्रश्न 7:
सिद्ध कीजिए कि =u + at
उत्तर:
माना किसी वस्तु का प्रारम्भिक वेग v है, जो । समयान्तराल के बाद v हो जाता है। त्वरण की परिभाष से,

प्रश्न 8:
असमान अथवा परवर्ती त्वरण से क्या तात्पर्य है ? धनात्मक तथा ऋणात्मक त्वरण क्या है।
उत्तर:
असमान या परिवर्तीत्वरण-यदि समान समयान्तरालों में वस्तु के वेग में परिवर्तन असमान हो, तो वस्तु का त्वरण असमान अंथवा परिवर्ती कहा जाता है। चित्र 3.20 में धनात्मक, ऋणात्मक तथा शून्य त्वरण वाली गति के लिए गति-समय ग्राफ दर्शाया गया है। इन ग्राफों में ऊपर की ओर जाती हुई वक्र धनात्मक

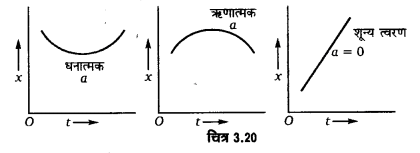
यदि समय के साथ वस्तु का वेग बढ़ता है तो उसमें उत्पन्न त्वरण धनात्मक कहलाता है और यदि वस्तु का वेग घटता है तो उत्पन्न त्वरण ऋणात्मक कहलाता है। ऋणात्मक त्वरण को मन्दन (retardation) भी कहते हैं।

विस्तृत उत्तरीय प्रश्न

प्रश्न 1:
सरल रेखा में गतिमान किसी कण के स्थिति-समय ग्राफ से क्या तात्पर्य है? ये कितने प्रकार के होते हैं? स्थिति-समय ग्राफ की सहायता से गतिमान कण के वेग का निर्धारण किस प्रकार किया जाता है? स्पष्ट कीजिए।
उत्तर:
स्थिति-समय ग्राफ-समय के सापेक्ष, सरल रेखा में गतिमान किसी कण की स्थिति को प्रदर्शित करने वाला ग्राफ वस्तु का स्थिति-समय ग्राफ कहलाता है। स्थिति समय ग्राफ अग्र दो प्रकार का होता है
(i) एकसमान गति का स्थिति-समय ग्राफ तथा
(ii) असमान गति का स्थिति-समय ग्राफ। सरल रेखा में गतिमीन किसी कंण की गति को उसके स्थिति-समय ग्राफ द्वारा व्यक्त किया जा सकता है। इसके लिए समय (t) को X-अक्ष पर तथा कण की स्थिति (x) को Y-अक्ष पर लेते हैं।
एकसमान गति के लिए स्थिति-समय ग्राफ-एकसमान गति (एकसमान वेग से गति) के लिए स्थिति-समय ग्राफ, समय-अक्ष के साथ एक निश्चित कोण पर झुकाव लिए सरल रेखा प्राप्त होती है। (चित्र 3.21)

स्थिति-समय ग्राफ से वेग का निर्धारण:
मान लीजिए एक, x,… सरल रेखा में एकसमान गति करते हुए कण का स्थिति-समय ग्राफ चित्र 3.21 में प्रदर्शित सरल रेखा OAB है। माना कि क्षणों t₁ तथा t₂ के संगत कण की स्थितियाँ क्रमशः व हैं, तब ६ समयान्तराल (t₂ – t₁) के लिए कण का स्थिति परिवर्तन


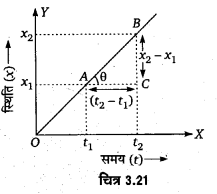
∴ वस्तु का वेग = स्थिति-समय वक्र का ढाल
अत: सरल रेखा में एकसमान गतिं करते कण का वेग, कण के स्थिति-समय ग्राफ के ढाल के बराबर होता है।
असमान गति के लिए स्थिति-समय ग्राफ-असमान गति । (परिवर्ती वेग से गति) के लिए स्थिति-समय ग्राफ एक वक्र (curve) के रूप में प्राप्त होता है (चित्र 3.22)।

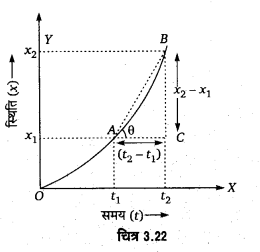
स्थिति-समय ग्राफ से औसत वेग का निर्धारण-मान लीजिए कि सरल रेखा में असमान गति से गतिमान केण का ए स्थिति-समय ग्राफ चित्र 3.22 में प्रदर्शित वक्र OAB है। माना कि क्षणों t₁ वे t₂ के संगत कण की स्थितियाँ क्रमशः

अतः किसी निश्चित समयान्तराल में वस्तु का औसत वेग उसके स्थिति-समय ग्राफ में उस निश्चित समयान्तराल के संगत वस्तु की स्थितियों को मिलाने वाली जीवा की प्रवणता के बराबर होता है। इस प्रकार, असमान गति के लिए प्राप्त स्थिति-समय ग्राफ के किन्हीं दो बिन्दुओं को मिलाने वाली जीवा की प्रवणता, उस समयान्तराल के लिए औसत वेग को प्रदर्शित करती है।

स्थिति-समय,ग्राफ से तात्क्षणिक वेग का निर्धारण:
यदि समयान्तराल (t₂– t₁) सूक्ष्म हो तब ग्राफ पर बिन्दु B, बिन्दु A के निकट आ जाता है। समयान्तराल ∆t के अत्यन्त सूक्ष्म (∆t ⇒ 0) होने पर बिन्दु A व B लगभग सम्पाती होकर ग्राफ को बिन्दु A पर स्पर्श करते हैं तथा जीवा AB, बिन्दु A पर स्पर्श रेखा में परिवर्तित हो जाती है।
अत: समय t₁ पर वस्तु का तात्क्षणिक वेग = बिन्दु A पर स्पर्श रेखी की प्रवणता = tan α

प्रश्न 2:
वेग-समय ग्राफ से गतिशील वस्तु का विस्थापन तथा दूरी उदाहरण सहित ज्ञात कीजिए।
उत्तर:
वेग-समय आफसे गतिशील वस्तु का विस्थापन तथा दूरी ज्ञात करना–कोई वस्तु जब गति में आती है तो उसका वेग बढ़ता है – तथा जब वस्तु को रोकना शुरू करते हैं तो वेग घटता है। स्पष्ट है कि वस्तु का वेग धनात्मक, ऋणात्मक व शून्य हो सकती है। वेग धनात्मक होने पर वेग-समय ग्राफ (OP) अक्ष के ऊपर की ओर तथा वेग ऋणात्मक होने पर ग्राफ (QR) अक्ष से नीचे की ओर होगा (चित्र 3.23)।

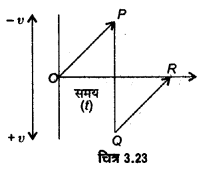
वेग-समय ग्राफ (v-t) तथा समय अक्ष के बीच घिरा क्षेत्रफल तय चित्र 3.23 की गई दूरी को बताता है। यदि क्षेत्रफल समय अक्ष के ऊपर है, तो यह मूल बिन्दु से दूरी को दर्शाता है, परन्तु यदि क्षेत्रफल समय-अक्ष के नीचे है, तो यह मूल बिन्दु की ओर दूरी को दर्शाता है। अतः कुल दूरी ज्ञात करने के लिए सभी क्षेत्रफलों को जोड़ देते हैं, जबकि विस्थापन ज्ञात करने के लिए समय-अक्ष के ऊपर के क्षेत्रफल धनात्मक व समय-अक्ष के नीचे के क्षेत्रफल ऋणात्मक लेते हैं।

उदाहरण–एक कार कीं, गति का वेग-समय ग्राफ चित्र 3.24 में प्रदर्शित है। ज्ञात कीजिए
(i) 5 सेकण्ड में विस्थापन तथा
(ii) 5 सेकण्ड में चलित दूरी।

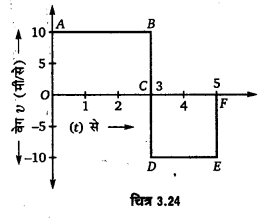
हल:
(i) 5 सेकण्ड में विस्थापन = क्षेत्रफल OABC- क्षेत्रफल CDEF
= 3×10- 10×2= 30- 20 = 10 मीटर,
(ii) 5 सेकण्ड में चलित दूरी = क्षेत्रफल OABC+ क्षेत्रफल CDEF
= 30+ 20 = 50 मीटर

प्रश्न 3:
किसी गतिमान वस्तु के वेग-समय ग्राफ से क्या तात्पर्य है। वेग-समय ग्राफ से वस्तु का विस्थापन तथा वस्तु का त्वरण किस प्रकार ज्ञात किया जाता है? स्पष्ट कीजिए।
उत्तर:
वेग-समय ग्राफ: किसी गतिमान वस्तु के वेग तथा समय के बीच खींचे गए ग्राफ को वस्तु का वेग-समय ग्राफ कहते हैं। अतः स्पष्ट है कि किसी वस्तु का वेग-समय ग्राफ, समय के साथ वस्तु के वेग में होने वाले परिवर्तन को प्रदर्शित करता है।

एकसमान गति के लिए वेग-समय ग्राफ:
एकसमान गति (एकसमान वेग से गति) के लिए वेग-समय ग्राफ, समय अक्ष के समान्तर एक सरल रेखा प्राप्त होती है (चित्र 3.25)

वेग-समय ग्राफ से विस्थापन का निर्धारण-किसी निश्चित समयान्तराल में वस्तु का विस्थापन, उसके वेग-समय वक्र तथा समय अक्ष के बीच घिरे क्षेत्रफल के बराबर होता है।
एकसमान वेग से गति के लिए वेग-समय ग्राफ, सरल रेखा AB प्राप्त होती है। समय t₁ व t₂ पर वस्तु

एकसमान त्वरित गति के लिए वेग-समय ग्राफ:
एकसमान त्वरित गति के लिए वेग-समय ग्राफ समय-अक्ष के साथ एक निश्चित क्रोण पर झुकाव लिए सरल रेखा के रूप में होता है (चित्र;3.26)। वेग-समय ग्राफ से त्वरण ज्ञात करना – मान लीजिए कि एकसमान त्वरण से गतिमान किसी वस्तु का वेग-समय ग्राफ एक प्रदर्शित किया गया है।

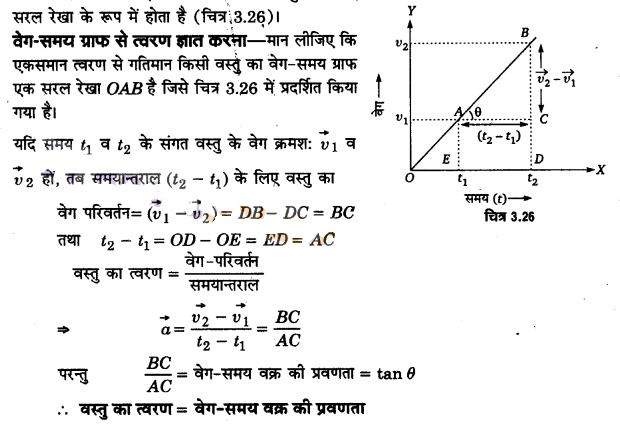
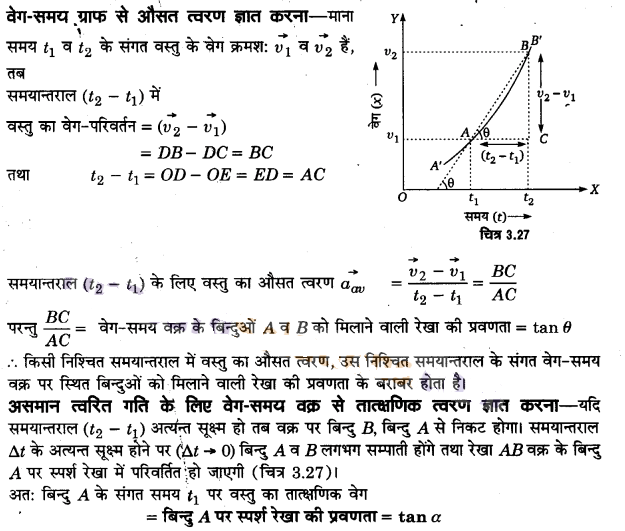
असमान त्वरित गति के लिए वेग-समय ग्राफ एक वक्र के रूप में होता है जैसा कि चित्र 3.27 में प्रदर्शित किया गया है।

प्रश्न 4:
ग्राफीय विधि द्वारा एकसमान त्वरित गति से गतिमान वस्तु की गति की समीकरणे व्युत्पन्न कीजिए।
या
एकसमान त्वरण से गतिमान वस्तु के लिए, ग्राफीय विधि से निम्नलिखित सम्बन्ध स्थापित कीजिए

उत्तर:
ग्राफ द्वारा गति के समीकरण स्थापित करना
माना कोई वस्तु प्रारम्भिक वेग u तथा अचर त्वरण a से चलना प्रारम्भ करती है और t समय पश्चात् वस्तु का वेग v हो जाता है। यदि समय को X-अक्ष पर तथा वेग को Y-अक्ष पर निरूपित किया जाए, तो वस्तु का समय-वेग ग्राफ पर झुकी हुई सरल रेखा BA के रूप में प्राप्त होली है (चित्र 3.28)।
इसकी सहायता से गति के समीकरणों को निम्न प्रकार से ज्ञात करते हैं

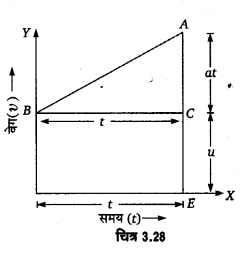
(i) गति का प्रथम समीकरण-माना t= 0 समय पर
वस्तु का प्रारम्भिक वेग u = OB= EC
समय (t) माना समय पश्चात् वस्तु का अन्तिम वेग
(ν) = EA
वेग-परिवर्तन में प्रयुक्त समय (t) = OE = BC
हम जानते हैं कि, वस्तु का त्वरण समय-वेग ग्राफ की रेखा के ढाल से ज्ञात होता है।
अतः वस्तु का त्वरण (a) = रेखा BA को ढाल

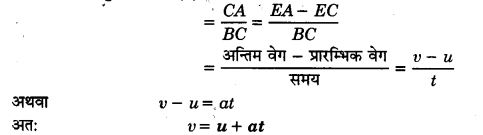
(ii) गति का द्वितीय समीकरण:
माना t = 0 से t समय तक वस्तु 8 दूरी तय करती है। यह दूरी t=0 से है समय तक वस्तु के समय-वेग ग्राफ तथा समये-अक्ष के बीच घिरे भाग का क्षेत्रफल
के बराबर होती है। अतः वस्तु द्वारा चली गई दूरी

(iii) गति का तृतीय समीकरण

प्रश्न 5:
कलन विधि से एकसमान त्वरित गति के समीकरणों की स्थापना कीजिए।
उत्तर:
कलन विधि से एकसमान त्वरित गति के समीकरणों की स्थापना-माना एक वस्तु एक सरल रेखा में एकसमान त्वरण a से गति कर रही है; समय t= 0 पर इसका प्रारम्भिक वेग ॥ तथा समय पश्चात् यह ν हो जाता है। माना इस है समय में वस्तु का विस्थापन s है।

(i) प्रथम समीकरण- माना गतिशील वस्तु के वेग में अति अल्प समय ∆t में परिवर्तन ∆ν है।
t समय पर वस्तु का त्वरण ।

(ii) द्वितीय समीकरण–माना गतिशील वस्तु का विस्थापन अल्प समयान्तराल ∆t में ∆s है तो क्षण t पर

(iii) तृतीय समीकरण-हम जानते हैं कि

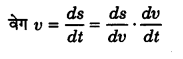
प्रश्न 6:
एकसमान त्वरण से गति करते हुए किसी वस्तु द्वारा किसी विशेष सेकण्ड में चली गई दूरी के लिए व्यजंक प्राप्त कीजिए।
उत्तर:
माना सरल रेखीय गति करते हुए पिण्ड की 7वें सेकण्ड में दूरी ज्ञात करनी है, तो पिण्ड द्वारा ॥ सेकण्ड में चली गई दूरी में से (n – 1) सेकण्ड में चली गई दूरी को घटा दिया जाता है। माना किसी वस्तु का प्रारम्भिक वेग ॥ है जो एकसमान त्वरण a से चलकर t सेकण्ड में s दूरी तय करती है, तब गति के सूत्र से

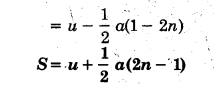
प्रश्न 7:
निम्न चित्र में प्रदर्शित समय-वेग ग्राफ से ज्ञात कीजिए

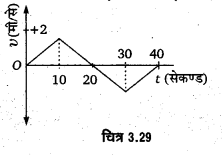
(i) 0 से 10 सेकण्ड का औसत त्वरण
(ii) 40 सेकण्ड में चली गई दूरी तथा विस्थापन
हल:

प्रश्न 8:
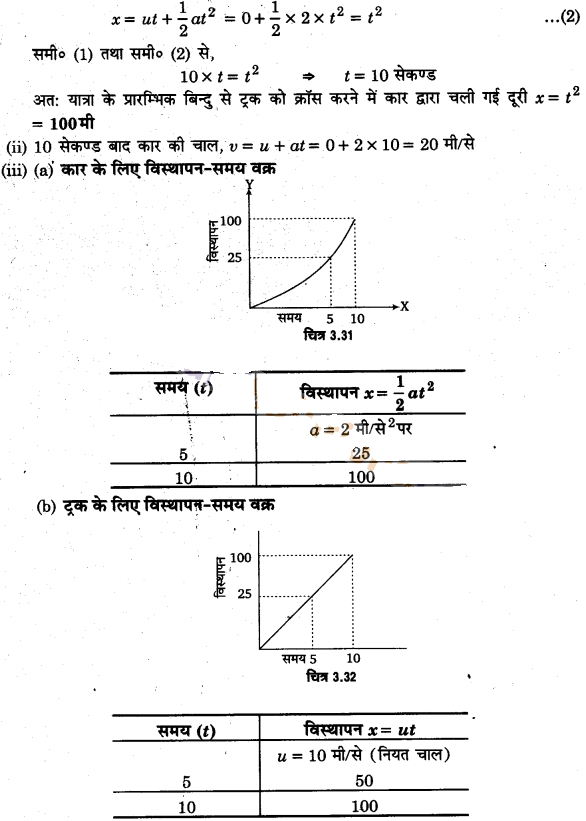
ट्रैफिक-सिग्नल के हरा होते ही एक कार 2 मी/से² के त्वरण से गति प्रारम्भ करती है। उसी क्षण एक ट्रक 10 मी/से की नियत चाल से कार को क्रॉस करता है।
(i) यात्रा के प्रारम्भिक बिन्दु से कार कितनी दूरी पर ट्रक को क्रॉस करेगी?
(ii) इस क्षण कार कितनी तेज चल रही होगी?
(iii) प्रत्येक गाड़ी के लिए विस्थापन-समय वक्र खींचिए।
हल:
दिया है, कार का त्वरण (a) = 2 मी/से², प्रारम्भिक वेग (u) = 0, ट्रक की नियत चाल (u) = 10 मी/से

(i) ट्रक को क्रॉस करने के लिए, कार द्वारा चली गई दूरी, टूक द्वारा चली गई दूरी के बराबर होगी।
माना कार t सेकण्ड बाद ट्रक को क्रॉस करेगी
इसलिए t सेकण्ड में ट्रैक द्वारा चली गई दूरी = u’ t = 10 x t …(1)
तथा t सेकण्ड में त्वरित कार द्वारा चली गई दूरी

प्रश्न 9:
आपेक्षिक वेग से आप क्या समझते हैं? आपेक्षिक वेग के लिए सूत्र का निगमन कीजिए।
उत्तर:
आपेक्षिक वेग-जब दो वस्तुएँ A तथा B क्रमश: तथा वेग से गतिमान होती हैं तो प्रति सेकण्ड उनके बीच के विस्थापन में होने वाले परिवर्तन को आपेक्षिक वेग कहते हैं।
सूत्र का निगमन:

We hope the UP Board Solutions for Class 11 Physics Chapter 3 Motion in a Straight Line ( सरल रेखा में गति) help you. If you have any query regarding UP Board Solutions for Class 11 Physics Chapter 3 Motion in a Straight Line ( सरल रेखा में गति) drop a comment below and we will get back to you at the earliest.